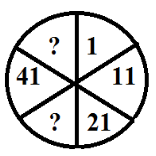
Дидактичний матеріал до заняття з теми "Арифметична прогресія"

Определите каких линий в буквах не хватает и прочитайте высказывание
французского математика Рене Декарта.

Проверьте свою смекалку и прочитайте тему нашего занятия: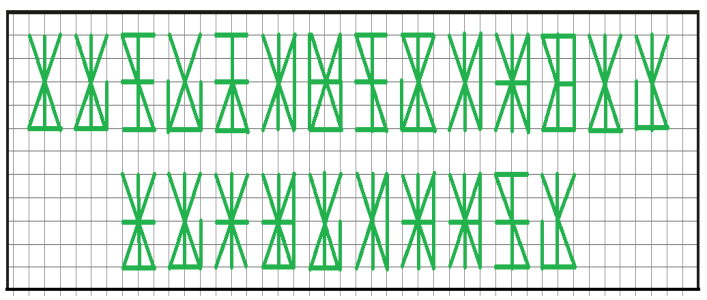

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
19 |
27 |
|
|
|
|
|
12 |
20 |
28 |
|
|
|
|
|
13 |
21 |
? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 1:
- найти закономерность в расположении
чисел, дополните таблицу;
- выпишите последовательности,
которые найдете;
- определите как получается каждое
новое число.
|
? |
|
28 |
|
? |
||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
16 |
|
d |
|
40 |
||||
|
|
||||||||
|
|
|
|
|
|||||
|
10 |
|
4 |
|
46 |
||||
|
|
||||||||
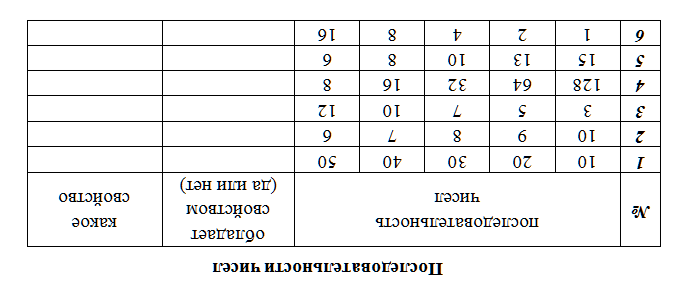
Задание 2:
- сколько здесь арифметических
прогрессий?
- найти разность а/п d;
- вставьте пропущенные члены а/п;
- запишите а/п.
_________________________________
_________________________________
Арифметической прогрессией называется последовательность, каждый член
которой, начиная со второго, равен предыдущему члену, к которому прибавляют одно и тоже число.
Это число называют разность а/п и обозначают d.
Основные элементы арифметической прогрессии: _______ и ______ (a1 и d)
|
Как найти разность а/п: |
d = |
d = an - an-1 |
|
Как найти n-ый член а/п: |
an = |
an = a1 + d (n - 1) |
|
1. Понятие арифметической прогрессии Посмотрите, подумайте и определите по какому правилу составлены последователь-ности чисел: Пример 1: 1 2 3
- определение а/п |
Задание всем учащимся: 1) найти неизвестные числа (?) 2) как найти d? (d=____________) – формула
а) d 0; б) d 0? 4) определите какими являются последовательности в примере 1. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. Понятие разности арифметической прогрессии (d) 1. Бесконечные и конечные а/п. Убывающие и возрастающие а/п. 2. Продолжите последовательности примера1 - столбик 1 – число, которое важно для последовательности; - столбик 2,3 – продолжить последователь-ность. |
Индивидуально (карточки) Карточка 1 Найдите и составьте возрастающую а/п. Вы- пишите её и проверьте себя.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. Работа по карточкам (по уровням): 1 уровень Найти и записать d, если
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 уровень Определите соответствие между данными: 1) 4; 12; 20; 28 d= 7 2) 79; 74; 69; 64 d= - 4 3) 16; 23; 30; 37 d= 8 4) 20; 16; 12; 8 d= - 5 |
Карточка 2 Найдите и составьте убывающую а/п:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 уровень Дописать неизвестные члены прогрессии: an: __ 17 25 33 __ вn: 20 18 __ __ __ сn: __ __ __ 30 39 kn*: 10 __ 22 __ __
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. Формула n-ого члена а/п: Пример 2. Запишите а/п: an : 25 30 35 __ __ … __ ...__ a1 a2 a3 a4 a5 a10 an
d = ____ a4 = ___ a5 = ___ ? Как найти: a10, a100, an? a10 = a100 = Формула an =_____________ |
1) Поиск a1: an = a1 + d (n - 1)
a1 = ________________(a1 = an - d (n - 1)) Записать a1 через a3: a1 = ______________________ Записать a1 через a7: a1 = ______________________ Заполнить самостоятельно таблицу:
2) Между числами 3 и 24 вставьте шесть чисел так, чтобы получилась арифметическая прогрессия. 3 __ __ __ __ __ __ 24 ______________________________________ ______________________________________
d= ______________ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5. Закрепление формулы: а) индивидуально (по карточкам)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
б) коллективно Задача. Облицовка первого этажа многоэтажного дома стоит 100 грн, а каждого следующего на 20 грн больше, чем предыдущего. Сколько будет стоить облицовка 10-го этажа? Решение a1= _____ d = _____ n = _____ a10 = _____________________________
В примере 2 берем формулы: a10 = ______________ = ______________ = _____ a100 = ______________ = ______________ = _____
? Сформулируйте другие вопросы к задаче о доме: - поиск … - поиск …
|
6. Домашнее задание (* опережающее задание) №1. Дана арифметическая прогрессия: 3 7 11 … … 87. Найти: 1) d; 2) сделать выводы об арифметической прогрессии; 3) принадлежит ли арифметической прогрессии число 43 и 53? 4) найти 11-ый член этой прогрессии; 5) сколько членов содержит эта арифметическая прогрессия? 6*) найти сумму всех членов заданной арифметической прогрессии. |


про публікацію авторської розробки
Додати розробку