Підсумкова контрольна робота
Підсумкова контрольна робота з алгебри, 9 клас. Варіант – 1
1. У ящику є 20 кубиків, пронумерованих від 1 до 20. Яка ймовірність того, що номер навмання взятого з ящика кубика буде кратним числу 7? (0,5)
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
2. Знайти медіану вибірки 7; 15; 12; 23; 31; 17; 25; 31. (0,5)
А) 18; Б) 19; В) 18; Г) 20.
3.Розв'язати нерівність: 6х < 16 – 2х. (0,5)
А) хє(2; +∞) Б) хє(-∞; -2) В) хє (-∞; -2] Г) хє(-∞; 2)
4.(bn)- геометрична прогресія, b₁=-32, q=-0,5. Знайдіть п'ятий член прогресії. (0,5)
А)-1; Б) 1; В) -2; Г) 2.
5. Графік функції ![]() паралельно пересли вниз на 3 одиниці і праворуч на 9 одиниць. Графік якої фукції отримаємо? (0,5)
паралельно пересли вниз на 3 одиниці і праворуч на 9 одиниць. Графік якої фукції отримаємо? (0,5)
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
6. Знайти кількість цілих розв'язків нерівності: -12<8х – 4 ≤12. (0,5)
А) 4 Б) 2 В) 1 Г) 3
7.Знайти суму нескінченної геометричної прогресії ![]() , якщо
, якщо ![]() ,
, ![]() . (0,5)
. (0,5)
А)36 Б) -21,6 В) -36 Г) -20,25
8. Оцінити значення виразу 2х + у, якщо 1,5<х<3 і 3<у<5. (0,5)
А) 4,5<2х+у<8 Б) 8<2х+у<9 В) 6<2х+у<11 Г) 6<2х+у<8
9. Розв'яжіть нерівність х2 – 49![]() . (0,5)
. (0,5)
А) (-∞;7) U(7;+∞); Б) (-∞;-7] U [7;+∞); В)(-∞;-7) Г)(-7;7)
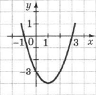 10. На малюнку зображено графік функції у=х2-2х-3.
10. На малюнку зображено графік функції у=х2-2х-3.
Вказати проміжок, на якому функція набуває додатніх значень .
А) (-∞;-1]U[3;+∞); Б) 3;+∞); В) (-1; 3); Г) (-∞;-1)U(3;+∞)
11.Розв'язати нерівність: -2х²+5х ≥ 2. (1б)
12.Знайти суму двадцяти перших членів арифметичної прогресії, якщо ![]() ,
, ![]() (2б)
(2б)
13. Розв'яжіть систему рівнянь: 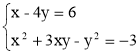 (2б)
(2б)
14.Знайти область визначення функції 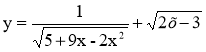 . (2б)
. (2б)
Підсумкова контрольна робота з алгебри, 9 клас. Варіант – 2
1. У ящику є 30 пронумерованих від 1 до 30 жетонів. Яка ймовірність того, що номер навмання взятого жетона буде кратним числу 7? (0,5)
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
2. Знайти середнє значення вибірки: 12; 10; 8; 11; 9; 12; 10; 8. (0,5)
А) 11 Б) 9 В) 10 Г) 12
3.Розв'язати нерівність: 5х > 18 – 4х. (0,5)
А) хє(-∞; 2) Б) хє(2; +∞) В) хє[2; +∞) Г) хє(-2; +∞)
4.(bn)- геометрична прогресія, b₁=-81, ![]() . Знайдіть четвертий член прогресії. (0,5)
. Знайдіть четвертий член прогресії. (0,5)
А) 1; Б) -1; В) 3; Г) -3.
5. Графік функції у=х² паралельно перенесли на 2 одиниці вгору і на 3 одиниці праворуч. Графік якої функції отримаємо? (0,5)
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
6. Знайти кількість цілих розв'язків нерівності: -16≤7х – 4 <12. (0,5)
А) 4 Б) 3 В) 2 Г) 1
7.Знайти суму нескінченної геометричної прогресії ![]() , якщо
, якщо ![]() ,
, ![]() . (0,5)
. (0,5)
А) -7,2 Б) ![]() В) 7,2 Г)
В) 7,2 Г) ![]()
8. Оцінити значення виразу х + 2у, якщо 4<х<6 і 0,5<у<2. (0,5)
А) 4,5<х+2у<8 Б) 5<х+2у<10 В) 8,5<х+2у<14 Г) 6<х+2у<8.
9. Розв'яжіть нерівність х2 – 16 ≤0. (0,5)
А) [-4;4]; Б) (-4;4); В) (-∞;4]; Г) (-∞;4]U[4;+∞).
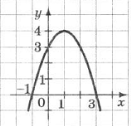 10. На малюнку зображено графік функції у=-х2+2х+3.
10. На малюнку зображено графік функції у=-х2+2х+3.
Вказати проміжок, на якому функція набуває від'ємних значень.
А) (-∞;-1]U[3;+∞); Б) (-∞;-1)U(3;+∞); В) (-1;0); Г) (-1;3)
11.Розв’язати нерівність: -2х² ≥ х – 6 . (1б)
12.Знайти суму тридцяти перших членів арифметичної прогресії, якщо ![]() , а різниця прогресії
, а різниця прогресії ![]() (2б)
(2б)
13. Розв'яжіть систему рівнянь: 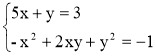 (2б)
(2б)
14.Знайти область визначення функції  (2б)
(2б)


про публікацію авторської розробки
Додати розробку
