ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ЯК МАТЕМАТИЧНА МОДЕЛЬ РЕАЛЬНИХ ПРОЦЕСІВ

ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ЯК МАТЕМАТИЧНА МОДЕЛЬ РЕАЛЬНИХ ПРОЦЕСІВ

1. Вступ

2. Поняття про математичну модель процесу.

3. Класифікація математичних моделей

4. Основні вимоги, що пред'являються до математичної моделі.

5. Істоія появи диференціальних рівнянь

6.  Поняття диференціального рівняння.

7. Диференціальні рівняння як математичні моделі.

8. Приклади використання диференренціальних рівнянь для  моделювання реальних процесів

9. Світоглядне значення однаковості диференціальних рівнянь, що описують різні процеси.

10. Висновок

11. Список використанних джерел

Вступ

Поняття, створені сучасною математикою, часто здаються досить далекими від реального світу. Але саме з їх допомогою людям вдалося проникнути в таємниці будови атомного ядра, розрахувати рух космічних кораблів, створити весь той світ техніки, на якій базується сучасне виробництво. Одним з основних методів пізнання природи є досвід, експеримент. За допомогою експериментів були встановлені багато законів природи (закон збереження речовини і енергії, періодична система елементів Д. І. Менделєєва і т. д.). Однак не завжди доцільно проводити експеримент. За останнє століття в самих різних галузях науки і техніки все більшу роль став грати метод математичного моделювання.

Щоб вивчити якесь явище природи або роботу машини, попередньо вивчають всілякі зв'язки між величинами, їх характеризують. Потім отримані зв'язки висловлюють математично і приходять до системи рівнянь. Вирішуючи ці рівняння або системи рівнянь, вчені та інженери роблять висновки про те, як надалі буде розвиватися це явище або як буде працювати машина, що треба зробити, щоб отримати необхідні результати.

При цьому рівняння і системи рівнянь бувають алгебраїчними і диференціальними. Щоб отримати рівняння, що допускають рішення, доводиться спрощувати завдання, відкидаючи деякі величини як несуттєві. Але чим точніше потрібен результат, тим більше величин доводиться враховувати, тим складніше виходить математична модель.

Математичні моделі, які будували в XIX столітті, були порівняно простими. Але зростаючі вимоги до точності відповіді, розвиток техніки, пізнання різноманітних явищ привели до створення все більш складних математичних моделей.

 Поняття про математичну модель процесу

Математичне моделювання - метод дослідження процесів або явищ шляхом створення їхніх математичних моделей і дослідження цих моделей.

В основу методу покладено ідентичність форми рівнянь і однозначність співвідношень між змінними в рівняннях оригіналу і моделі, тобто, їхню аналогію. Математичні моделі досліджуються, як правило, із допомогою аналогових обчислювальних машин, цифрових обчислювальних машин,комп'ютерів.

На початку 60-их років було розроблено один із методів математичного моделювання - квазіаналогове моделювання. Цей метод полягає в дослідженні не досліджуваного явища, а явища або процесу іншої фізичної природи, яке описується співвідношеннями, еквівалентними відносно отримуваних результатів.

Математичне моделювання тією чи іншою мірою застосовують всі природничі і суспільні науки, що використовують математичний апарат для одержання спрощеного опису реальності за допомогою математичних понять. Математичне моделювання дозволяє замінити реальний об'єкт його моделлю і потім вивчати останню. Як і у разі будь-якого моделювання, математична модель не описує явище абсолютно адекватно, що залишає актуальним питання про застосовність отриманих таким шляхом даних. Математичне моделювання широко застосовується у гірництві, геології, для вивчення і аналізу процесів переробки корисних копалин

Класифікація математичних моделей

Математична модель — це наближений опис об'єкта за допомогою математичної символіки. 

Їх можна систематизувати (класифікувати) за різними ознаками.

1. Класифікація за галузями наук: математичні моделі у фізиці, біології, соціології і т. п.

2. Класифікація за математичним апаратом: моделі, засновані на засто­суванні звичайних диференціальних рівнянь, диференціальних рівнянь у част­кових похідних, стохастичних методів, дискретних алгебраїчних перетворень і т. д. Це — класифікація математика, що займається апаратом математичного моделювання.

3. Класифікація за метою (цілями) моделювання.

3.1. Дескриптивні моделі (від лат. «descriptivus» — опис) — це моделі для опису різних процесів, об'єктів. Наприклад, закони класичної фізики Ньютона.

3.2. Оптимізаційні моделі. Це моделі для керування об'єктами та при­йняття рішень.

Наприклад, змінюючи тепловий режим у зерносховищі, ми можемо піді­брати його таким чином, щоб досягнути максимального збереження зерна, тобто оптимізувати процес.

3.3. Багатокритеріальні моделі. Це моделі для розв'язування задач,в яких є не одна, а декілька цільових функцій.

Наприклад, знаючи ціни на продукти і потребу людини в їжі, треба орга­нізувати харчування великих груп людей (в армії, будинку відпочинку і т. д.) найкорисніше і найдешевше. Зрозуміло, що такі цілі не співпадають, тобто при моделюванні буде декілька

3.4. Ігрові моделі. Це моделі для опису і дослідження так званих кон­фліктних ситуацій, в яких різні учасники мають інтереси, що не співпадають.Наприклад, два воєначальники перед боєм в умовах наявності непевної інформації про супротивника повинні розробити план: в якому порядку вводити в бій ті чи інші частини і т. д., враховуючи і можливу реакцію ворога.

3.5. Імітаційні моделі. Це моделі для дослідження складних систем. Тутпроцес функціонування складної системи подається у вигляді певного ал­горитму, який реалізується комп'ютером.

Імітаційні моделі широко використовуються в сучасній фізиці, зокрема, для дослідження термоядерних процесів.

Властивості математичних моделей:

1) математична модель повинна бути адекватною (відповідною) досліджу­ваному об'єкту з точки зору тих властивостей (характеристик), які цікавлять дослідника;

2) математична модель не визначається однозначно досліджуваним об'єктом;

3) математична модель лише наближено описує досліджуваний об'єкт; для одного і того ж об'єкта можна побудувати різні математичні моделі з різним ступенем наближення;

4) математична модель універсальна в тому плані, що одну і ту ж матема­тичну модель можна використовувати для досліджень у різних галузях людської діяльності.

Основні вимоги, що пред'являються до математичної моделі

До математичних моделей пред'являються наступні основні вимоги:

- універсальність (характеризує повноту відображення в ній властивостей реального об'єкта);

- точність (оцінюється мірою збігу значень вихідних параметрів реального об'єкта і значень тих же параметрів, розрахованих за допомогою моделі);

- адекватності (здатність моделі відображати задані властивості об'єкта з погрішністю, не вище заданою);

- економічність (характеризується витратами обчислювальних ресурсів на її реалізацію);

- вичислимости (можливість ручного або за допомогою ЕОМ дослідження якісних і кількісних закономірностей функціонування об'єкта (системи) );

- модульність (відповідність конструкцій моделі структурним складовим об'єкта (системи));

- алгоритмизируемости (можливість розробки відповідних алгоритму і програми, реалізуючий математичну модель на ЕОМ);

- наглядності (зручне візуальне сприйняття моделі).

Основними вимогами, що пред'являються до математичних моделей, є вимоги адекватності, універсальності і економічності, точності.

Адекватність моделі -здатність відображати задані властивості об'єкта з погрішністю не вище заданої. Модель вважається адекватною, якщо відображає задані властивості з прийнятною точністю.

 Точність визначається як міра збігу значень вихідних параметрів моделі і об'єкта. Точність моделі різна в різних умовах функціонування об'єкта. Ці умови характеризуються зовнішніми параметрами. У просторі зовнішніх параметрів виділити область адекватності моделі, де погрішність менше заданої гранично допустимої погрішності.

Визначення області адекватності моделей - складна процедура, що вимагає великих обчислювальних витрат, які швидко зростають із збільшенням розмірності простору зовнішніх параметрів. Ця задача по об'єму може значно перевершувати задачу параметричної оптимізації самої моделі, тому для об'єктів, що знову проектуються може вагатися.

Універсальність- визначається в основному числом і складом зовнішніх і вихідних параметрів, що враховуються в моделі.

Економічність моделі характеризується витратами обчислювальних ресурсів для її реалізації - витратами машинного часу і пам'яті.

Суперечність вимог до моделі володіти широкою областю адекватності, високій мірі універсальності і високій економічності зумовлює використання ряду моделей для об'єктів одного і того ж типу.

Істоія появи диференціальних рівнянь

У кінці XVII — на початку XVIII ст. різноманітні практичні і наукові проблеми привели до появи диференціальних рівнянь. Насам­перед це були диференціальні рівняння першого порядку, інтегруван­ня яких намагалися здійснити за допомогою функцій, що виражають скінченне число алгебраїчних дій або таких, що включають елементарні неалгебраїчні дії, наприклад оперування тригонометричними функ­ціями.

Найпростіші диференціальні рівняння з'явилися вже в працях Ісаака Ньютона (1643—1727) і Готфріда Лейбніца (1646—1716). Саме Лейбніцу і належить термін «диференціальне рів­няння». Диференціальні рівняння мають велике прикладне значення, вони є знаряддям дослідження багатьох задач природознавства і тех­ніки. їх широко використовують в механіці, астрономії, фізиці, у ба­гатьох задачах хімії, біології. Це пояснюється тим, що-досить часто об'єктивні закони, яким підпорядковуються певні явища (процеси), записують у формі диференціальних рівнянь, а самі ці рівняння є за­собом для кількісного вираження цих законів.

Наприклад, фізичні закони описують деякі співвідношення між ве­личинами, що характеризують певний процес, і швидкістю зміни цих величин. Іншими словами, ці закони виражаються рівностями, в яких е невідомі функції та їх похідні.

У XVIII ст. теорія диференціальних рівнянь відокремилася з ма­тематичного аналізу в самостійну математичну дисципліну, її успіхи пов'язані з іменами швейцарського вченого Іоганна Бернуллі (1667—1748), французького математика Жозефа Лагранжа (1736—1813) і особливо Леонарда Ейлера.

Перший період розвитку диференціальних рівнянь був пов'язаний з успішним розв'язуванням деяких важливих прикладних задач, що при­водять до диференціальних рівнянь, розробкою методів інтегрування різних типів диференціальних рівнянь і пошуком класів рівнянь, роз­в'язки яких можна подати у вигляді елементарних функцій або їх пер­вісних. Проте дуже швидко виявилося, що інтегрованих диференціаль­них рівнянь зовсім небагато. Це привело до розвитку власне теорії диференціальних рівнянь, яка займається розробкою методів, що дають змогу за властивостями диференціального рівняння визначити властивості і характер його розв'язку.

У зв'язку з потребами практики поступово розроблялися і спосо­би наближеного інтегрування диференціальних рівнянь. Ці методи дають зручні алгоритми обчислень з ефективними оцінками точності, а сучасна обчислювальна техніка дає змогу економічно і швидко звести розв'язування кожної такої задачі до числового результату.

Поняття диференціального рівняння

Звичайним диференціальним рівнянням називають рівняння, яке в собі зв'язує незалежну змінну х, функцію у(х) та похідні у'(х), уn(х) і має загальний вигляд F(x,y(x),y' (x), …, yn(x))=0  Диференцiальним рiвнянням (ДР) називається або звичайне диференцiальне рiвняння, або диференцiальне рiвняння з частинними похiдними. 

Порядок диференціального рівняння визначається порядком старшої похідної (n), яка входить до даного диференціального рівняння.

Загальним розв'язком диференціального рівняння називається функція, яка містить стільки сталих, який порядок диференціального рівняння, і підстановка якої в дане диференціальне рівняння перетворює його в тотожність, тобто має вигляд  y=f(x, C1, C2, …, Cn). 

Загальний розв'язок, який не розв'язаний відносно у(х) і має вигляд F(x,y,C1,C2,…,Cn)=0 називається загальним інтегралом диференціального рівняння.  

Розв'язок, знайдений із загального розвязку при фіксованих значеннях сталих C1,C2, …, Cn називається частинним розв'язком диференціального рівняння.  Одночасне задання диференціального рівняння і відповідної кількості початкових умов називається задачею Коші.  F(x,y,C1,C2, …, Cn)=0 y(x0)=y0; …. yn(x0)=yn(0) Звичайним диференцiальним рiвнянням першого порядку називається рiвняння вигляду F(x, y, y')=0. (1)

 Iнтегралом рiвняння (1) називається cпiввiдношення вигляду Φ(x, y)=0, якщо кожна неявно задана ним неперервно-диференцiйовна функцiя є розв'язком рiвняння (1). Рівняння, яке має вигляд (1) і не може бути зведене до простішого вигяду називається рiвнянням, нерозв'язним стосовно похiдної.

Якщо його можна записати у виглядi y' = f(x,y), то воно називається рiвнянням, розв'язаним стосовно похiдної.  Задача Коші для рівняння першого порядку містить лише одну початкову умову і має вигляд: F(x,y,y')=0 y(x0)=y0.  Рiвняння вигляду (2)  а змiннi x i y є "симетричними": можна припускати, що x – незалежна, а y – залежна змiнна, або, навпаки, y – незалежна, а x – залежна змiнна, називається рiвнянням в симетричнiй формі. Геометричний зміст диференціаьного рівняння першого порядку y'=f(x, y) (3) полягає в наступному. Дане рівняння встановлює зв ' язок ( залежність ) між координатами точки (x; y) і кутовим коефіцієнтом y' дотичної до інтегральної кривої, що проходить через цю точку .

Таким чином, рівняння y'=f(x, y) дає сукупність напрямів ( поле напрямів ) на декартовій площині Oxy. Крива, побудована на точках, в яких напрям поля однаковий, називається ізокліною. Ізоклінами можна користуватися для наближеної побудови інтегральних кривих . Рівняння ізокліни можна одержати, якщо покласти похідну рівну сталій y'=С f(x, y)=С - рівняння ізокліни. 

Iнтегральною лiнiєю рiвняння (3) називається графiк розв'язку цього рiвняння.  Звичайнi диференцiальнi рiвняння, розв'язки яких можна задати аналітично y=g(x), називаються iнтегровними рiвняннями.  

Рiвняння вигляду   (3)  називаються рiвняннями з вiдокремленними змiнними.  З них і розпочнемо знайомство з диференціальними рівняннями.

Процес знаходження розв'язків диференціального рівняння ще називають інтегруванням диференціального рівняння.

Диференціальні рівняння як математичні моделі.

Для дослідження складних процесів в об'єктах, що змінюються з

плином часу, застосовуються дескриптивні (описові) Математичні

моделі у вигляді диференціальних рівнянь (або систем диференціальних

рівняння.)

Рівняння моделей складаються на підставі фізичних, хімічних,

біологічних законів. Рішення таких систем диференціальних рівнянь є функціями часу і, отже, можуть описувати зміни в часі процесів, що відбуваються всередині модельованих об'єктів.

Моделі діляться на два основних типи:

•  з зосередженими параметрами

диференціальних рівнянь: ці моделі дійсні для

описи процесів, які не залежать від координат

(зосереджені в точці);

• з розподіленими параметрами у вигляді диференціальних

рівнянь з приватними похідними: їх рішення залежать як від

часу, так і від координат області рішення.

Рівняння класифікуються за кількістю координат області рішення:

• одновимірний;

• двовимірні (на площині);

• тривимірні (просторові).

ПРИКЛАДИ ВИКОРИСТАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ ДЛЯ МОДЕЛЮВАННЯ РЕАЛЬНИХ ПРОЦЕСІВ

1 Модель рекламної компанії

Фірма починає рекламувати новий товар або послугу. Зрозуміло, що прибуток від майбутніх продажів повинен з лишком покривати витрати на дорогу кампанію. Ясно, що спочатку витрати можуть перевищувати прибуток, оскільки лише мала частина потенційних покупців буде поінформована про новинку. Потім, при збільшенні числа продажів, вже можливо розраховувати на помітну прибуток, і, нарешті, настане момент, коли ринок насититься, і рекламувати товар, далі стане безглуздо.

Модель рекламної кампанії ґрунтується на наступних основних припущеннях. Вважається, що величина швидкість зміни часом числа споживачів, які дізналися про товар і готові купити його (t - час, що минув з початку рекламної кампанії, N(t) - кількість поінформованих клієнтів), - пропорційна числу покупців, ще не знають про нього, тобто величиною a1(t) (N0 - N(t)), де N0 - загальна кількість потенційних платоспроможних покупців, а1(t)>0 характеризує інтенсивність рекламної кампанії (фактично визначається витратами на рекламу в даний момент часу). Передбачається також, що дізналися про товар споживачі тим чи іншим чином поширюють отриману інформацію серед необізнаних, виступаючи як би додатковими рекламними «агентами» фірми. Їх внесок дорівнює величині a2 (t) N(t) (N0-N (t)) і тим більше, чим більше число агентів. Величина а2(t) > 0 характеризує ступінь спілкування покупців між собою (вона може бути встановлена, наприклад, з допомогою опитувань).

В результаті отримуємо рівняння

 ()*( (1)

При a1 (t) > > a2N(t) з (1) виходить модель типу моделі Мальтуса при протилежній нерівності-рівняння логістичної кривої

= Ndф = (t) dt,

Розглянемо модель в околиці точки N (t = 0) = N (0) = 0; t=0- (момент початку компанії), вважаючи, що N < < N0, a2 (t) N << a1 (t) то рівняння прийме вид=a1 (t) N0 і має рішення

N(t) = (t) dt (2)

задовольняє природному початковому умові при t=0. З (2) відносно легко вивести співвідношення між рекламними витратами і прибутком на самому початку кампанії. Позначимо через р величину прибутку від одиничного продажу, якою б вона була без витрат на рекламу. Вважаємо для простоти, що кожен покупець набуває лише одну одиницю товару. Коефіцієнт А1 (t) за своїм змістом - число рівнозначних рекламних дій в одиницю часу, наприклад, розклеювання однакових афіш. Через s позначимо вартість елементарного акту реклами. Тоді сумарний прибуток є

P=сN(t)=сN0 a1(t) dt (3)

а вироблені витрати

S=sa1(t) dt (4)

І в силу незалежності a1 від часу

Р = сN (t)=с ? N0 ? aa ? t;

S=s ? a1 ? t;

Отже, ми отримали найпростіші лінійні залежності прибутку від часу.

Зрозуміло, дані залежності не відображають реальну картину, що виникає в ході рекламної компанії. Робимо висновок, що в разі короткострокової моделі, при якій покупці не встигають передати інформацію про продукт, і при невеликих в порівнянні з оборотом фірми зарплатах на рекламу, прибуток зростає лінійно.

2 Витікання рідини з судин. Водяний годинник

Площа горизонтального перетину, якого є довільною функцією відстані перетину від дна судини.

Нехай висота рівня рідини в посудині в початковий момент часу t=0 дорівнює h метрів. Нехай, далі, площа перетину на висоті х дорівнює S (x), а площа отвору на дні судини є S.

Відомо, що швидкість витікання рідини U в той момент, коли висота її рівня дорівнює x, визначається рівністю U=k, де g=9,8 м/с2, k - коефіцієнт швидкості витікання рідини з отвору. На нескінченно малому проміжку часу dt витікання рідини можна вважати рівномірним, а тому за час dt витече стовпчик рідини, висота якого Udt і площа перерізу S, що в свою чергу викличе зниження рівня рідини в посудині на - dх.

В результаті цих міркувань приходимо до диференціального рівняння

ksdt = - S(x) dx; (5)

яке можна переписати у вигляді

dt=-dx; (6)

Вирішимо тепер наступну задачу. Циліндричний резервуар з вертикальною віссю висотою 6 м і діаметром 4 м має на дні круглий отвір радіусом 1/12 м. Потрібно встановити залежність рівня води в резервуарі від часу t, а також визначити час, протягом якого витече вся вода.

За умовами завдання S (x)=4р; S=1/144. Так як для води k=0,6, то рівняння (6) прийме вид dt = - dx;

Інтегруючи це диференціальне рівняння, приходимо до співвідношення     t= 434,304 ;яке і дає шукану залежність рівня води від часу t. Якщо тепер в останньому рівності покласти х=6, то отримаємо, що вся вода витече з резервуара приблизно через 18 хвилин.

Друге завдання полягає в наступному. Відомо, що стародавні водяні годинники представляли собою чашу (рис. 2), з якої через невеликий отвір на дні витікала вода. Такі годинники використовувалися в грецьких і римських судах для хронометрування промов адвокатів, щоб не допускати занадто довгих виступів. Потрібно знайти форму водяного годинника, при якій рівень води убував би в чаші з постійною швидкістю.

Задача легко вирішується за допомогою виведеного вище рівняння (6), яке ми тільки перепишемо у вигляді

Саме, враховуючи, що чашу можна розглядати як поверхню обертання, відповідно до позначень з рівняння (7) отримуємо, що

Де a=Ux=- проекція вільної поверхні рідини на вісь x, яка за умовою задачі є величина постійна. Звівши обидві частини рівняння (8) в квадрат приходимо до рівняння

x=cr4; (9)

де c=а2р2/(2gk2s2). Останнє означає, що форма поверхні водяного годинника виходить обертанням кривої (9) навколо осі х.

 Прогин і поворот перерізу балки

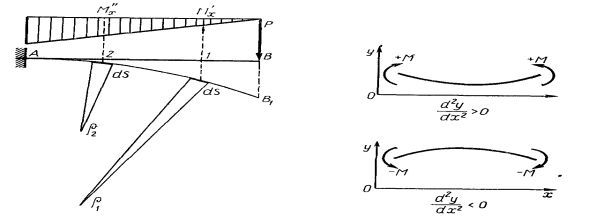
До проектуємих частин споруджень пред'являються вимоги не тільки до міцності, але і до твердості, тобто щоб їхні пружні деформації під дією навантаження були як можна меншими (у результаті великого прогину валів порушується правильність зачеплення зубчастих чи коліс виникають кромочні навантаження в підшипниках ковзання й ін.). Вивчення деформацій також необхідно при рішенні статично невизначених задач.

На мал. 1 зображена в перекрученому масштабі скривлена вісь балки, затисненої одним кінцем і завантаженої на іншому кінці зосередженою силою. Початок системи координат розташуємо в одній із крапок первісної осі балки, яку завжди будемо вибирати за вісь х; вісь у будемо направляти перпендикулярно до первісної осі балки нагору. Центр ваги О якого-небудь перетину з абсцисою х переміщається в точку O₁. Переміщення у центра ваги перетину по напрямку, перпендикулярному до осі балки, називається прогином балки в цьому перетині, чи прогином цього перетину балки. Оскільки прогини у звичайно малі в порівнянні з довжиною балки, то зсувом точки O₁ (нейтральний шар не змінює своєї довжини при вигині) убік від перпендикуляра до осі балки можна зневажити як величиною вже 2-го порядку малості. Тоді рівняння вигнутої осі балки буде

Y = f (x) (1)

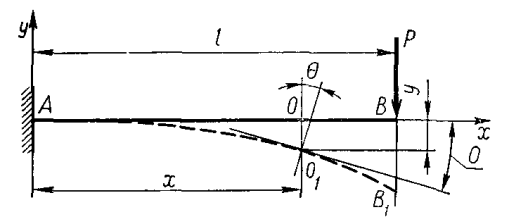
Мал. 1.

Найбільший прогин може служити мірилом того, наскільки спотворюється форма конструкції при дії зовнішніх сил (прогини, що допускаються, у залежності від призначення конструкції коливаються в межах      частки прольоту).

При деформації балки перетин, залишаючись плоским, повертається стосовно свого колишнього положення (1). Кут q, на який кожен перетин повертається стосовно свого первісного положення, називається кутом повороту перетину. Дотична до вигнутої осі балки (1) у точці O₁ складе з віссю х кут, рівний q, тобто це кут повороту поперечного переріза щодо первісного положення. З іншого боку, тангенс кута, утвореного дотичної до кривої у = /(х) з віссю х, дорівнює

      (2)

На практиці прогини звичайно дуже малі, при цьому кути q також дуже малі, тому можна прийняти tg q == q і тоді (2) запишемо так:

  (3)

тобто кут повороту перетину дорівнює першої похідної х від прогину у в цьому перетині.

Таким чином, вивчення деформації балки зводиться до одержання рівняння вигнутої осі у == f (х), а вже потім простим диференціюванням обчислимо кут повороту (3). Варто пам'ятати, що по своїй фізичній сутності пружна лінія вигнутої осі балки повинна бути кривою неперервною і гладкою, що рівнозначно вимозі, щоб функція у == f (х) і її перша похідна були неперервні усюди протягом осі балки.

Диференціальне рівняння вигнутої осі балки

Для того щоб визначити у == f (х), необхідно установити залежність деформації балки від зовнішніх сил, розмірів і матеріалу балки. При перебуванні нормальних і дотичних напружень у балці при вигині прийнята наступна формула:
 

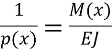  (4)

де р(х) — радіус кривизни ділянки вигнутої осі балки між двома суміжними перетинами на відстані х від початку координат; М (х) — згинальний момент у тім же перетині; EJ —твердість балки. Вплив Q (х) на деформацію балки невеликий, про що буде сказано нижче.

Зміна радіуса кривизни в залежності від зміни згинаючого моменту показана на мал. 2.

Для одержання рівняння вигнутої осі балки скористаємося відомим з диференціального числення вираженням кривизни кривої

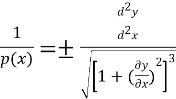   (5)

Зіставляючи вираження (4) і (5), знайдемо залежність між х, у, М(х), EJ

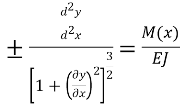
Це і є диференціальне рівняння вигнутої осі. Рівняння (6) — звичайне нелінійне диференціальне рівняння другого порядку, що інтегрується в еліптичній і інших спеціальних функціях. Способи інтегрування таких рівнянь викладені в курсах теорії пружності. У практичних додатках звичайно користаються наближеним рівнянням. Прогини звичайно малі, при цьому кути нахилу дотичних також малі. Якщо навіть припустити, що кут нахилу перетину досяг 1°, то tg 1°

Значення це настільки мале в порівнянні із одиницею, яка знаходиться в знаменнику лівої частини вираження (6), що їм можна зневажити.

Тоді рівняння (6) спрощується

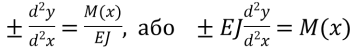 (7)

Це і є наближене диференціальне рівняння вигнутої осі балки. Воно дає цілком задовільні результати для більш твердих балок. Навіть при прогинах, рівної 1/10 довжини балки, погрішність досягає не більш 1,5 %.

Мал.2        Мал.3
 

Правило знаків для М(х) встановлено і не залежить від напрямку координатних осей   >0 , якщо убік позитивної осі у звернена увігнутість кривої і<0  - якщо випуклість (мал. 3).

Умовимося надалі завжди вісь у направляти нагору («+» — при напрямку у нагору, «—» — при напрямку вниз) і диференціальне рівняння (7) писати у виді

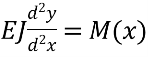    (8)

Для одержання з диференціального рівняння вигнутої осі рівняння прогинів у = f (x) необхідно зробити інтегрування рівняння (8).

Інтегруючи один раз, одержимо

)dx+C
 

Інтегруючи друг раз, маємо:

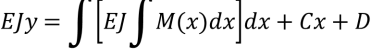
Таким чином, одержимо рівняння кутів повороту

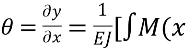 )dx+C]   (9)

і рівняння прогинів

  (10)

Мал. 4

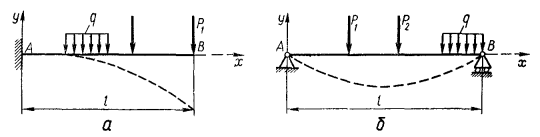
де С и D — довільні постійні інтегрування, для визначення яких необхідно мати принаймні хоча б дві умови де відомі значення функції у і її похідної. Ці умови називаються граничними умовами задачі.

Установимо граничні умови для консольної і простої балки (мал. 4). Незалежно від дії зовнішнього навантаження для кожної балки знайдемо дві граничні умови, з огляду на способи закріплення балки на кінцях.

1. Для консольної балки (мал. 4, а) прогин на лівому кінці дорівнює нулю; також дорівнює нулю кут нахилу дотичної q до осі. Таким чином, маємо наступні граничні умови:

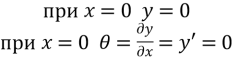  (11)

2 Для двохопорної балки (мал. 8.4 б) прогини на кінцях А и В звертаються в нуль. Одержуємо такі умови:

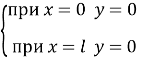     (12)

Визначивши з граничних умов (11) і (12) довільні постійні С и D і підставивши їх у рівняння (9) і (10), одержимо остаточне рівняння пружної лінії і кута повороту.

Світоглядне значення однаковості диференціальних рівнянь, що описують різні процеси

Диференціальні рівняння стали широко використовуватися не лише в математиці, але в багатьох інших науках. Отож, наскільки важливими є диференціальні рівняння і як часто ми їх зустрічаємо в реальному житті?! Можливо для декого це буде неочікувано, але насправді, диференціальні рівняння відіграють величезну роль в нашому житті і це стосується не тільки математиків, фізиків, але й людей, які зовсім не пов’язані з наукою. Їхню значущість можна оцінити з можливості математично описати, або моделювати, реальні життєві ситуації. Диференціальні рівняння описують різноманітні процеси в таких дисциплінах як екологія, хімічна кінетика, архітектура, фізика, машинобудування, демографія, механіка, електротехніка, будівництво, медицина, метрологія, економіка і взагалі, якщо існує явище зміни однієї величини відносно іншої, то воно може бути описане диференціальним рівнянням або системою рівнянь.

Тож розглянемо декілька реальних життєвих процесів.

 За допомогою диференціальних рівнянь можна математично описати процес розмноження чи вимирання популяцій. Нехай x(t) – кількісний стан популяції в момент t , A – число, яке відповідає кількості народжених, B – умираючих в одиницю часу. Тоді швидкість зміни координати x(t) задається формулою:

В (1.1)  і  можуть залежити від . Наприклад:

A=ax, B=bx (1.2)

Де a – коефіцієнт народжуваності, b – смертності. Маємо з (1.3)

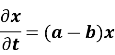
Розв’язок диференціального рівняння запишемо в вигляді

З розв’язку (1.4) видно, що при  популяція вижчваюча, а при  – вмираюча.

 (1.4)

Рівняння (1.3) в деяких випадках береться нелінійним

   (1.5)

Це рівняння Беруллі при  і його розв’язок запишеться в такому вигляді

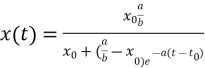     (1.6)

З формули (1.6) видно, що при При цьому можливі випадки

, та  ,

Рівняння (1.5) описує.

Можна говорити і про більш складні рівняння, системи рівнянь.

Розглянемо більш детально двух видову модель «хижак-жертва», яка була побудована для виявлення коливань рибних уловів в Адріатичному морі.

Нехай  –число великих риб-хижаків, y – число малих риб-жертв в момент часу t, тоді число риб-хижаків буде рости до тих пір, поки у них буде їжа. Якщо корму не буде вистачати, то кількість риб-хижаків буде зменьшуватися і тоді, починаючи з деякого моменту, буде рости число риб-жертв. Модель має вигляд

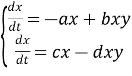   (1.7)

де a,b,c,d– додатні константи.

В (1.7) доданок виражає залежність прирісту великих риб від числа малих, – зменьшення числа малих риб від великих.

В біології, наприклад, можна знайти залежність площі S молодого листка, що має форму круга, від часу t . Відомо, що швидкість зміни площі dt dS в момент t пропорційна площі листка, довжині його обводу та косинусу кута між падаючим на листок сонячним променем і вертикаллю листка. Маємо модель

  (1.8)

де (t)  at  b  0, a,b – const,    , k – коефіцієнт пропорційності. Розв’язуючи рівняння (1.8), ми отримаємо таку залежність

        (1.9)

c – довільна стала. Також наше життя тісно пов’язане з економікою: купуємо товари, користуємося різними послугами, дехто можливо робить і продає свої ручні роботи. Завжди відбувається обмін товарів і грошей. В економіці це називається законом попиту і пропозиції і описується цей закон диференціальними рівняннями. Нехай p(t) – ціна, наприклад, на овочі, dt dp – тенденція формування ціни. Тоді, як попит так і пропозиція будуть функціями введених величин. Як показує практика, ці функції можуть бути різними. Часто попит q і пропозиція S задаються лінійними залежностями, наприклад

   (1.10)

Для того, щоб попит відповідав пропозиції необхідно ( p  S)

  (1.11)

Звідки

   (1.12)

Припустимо, що в момент t  0 1кг овочів коштував p(0)  1 грн. Тоді 1  c 10, c  9. Отже

    (1.13)

Це закон зміни ціни, щоб між попитом і пропозицією була рівновага. Існує ще безліч рівнянь, які описують найрізноманітніші процеси в різних областях науки.

Закони Кеплера руху планет.

Згідно закону всесвітнього тяжіння два тіла, які знаходятся на віддалі  друг від друга і які мають маси  і притягаються з силою

 (1.14)

де - константа тяжіння.

Опишемо рух планети з масою  навколо Сонця маси . Вплив других планет на них не будемо враховувати. (Мал 1.1).

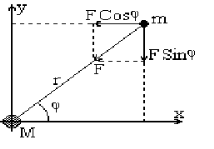
Сонце знаходиться в початку координат, а планета має положення  в момент часу . Використавши другий закон Ньютона маємо:

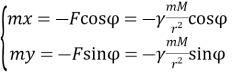  (1.15)

Враховуючи, що

Позначимо , прийдемо до системи

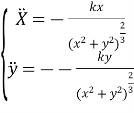       (1.16)

Без обмеження загальності візьмемо початкові умови:

  при t=0 (1.17)

Перейдемо до полярних координат:

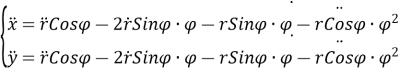
Позначивши отримані вирази в (1.10) будемо мати

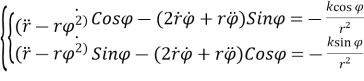
Помножимо перше рівняння на ,друге на  і складемо:

   (1.17)

Домножимо перше рівняння на  ,друге на  і складемо:

   (1.18)

Перепишемо в нових змінних умови (1.11):

Рівняння (1.13) перепишемо у вигляді

 (1.20)

 (1.21)

Звідки маємо

 (1.22)

Константа  має цікаву гнометричну інтерпретацію. З курсу математичного аналізу відомо, що площа сектора обчислюється за формулою

Звідки

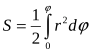 (1.23)

,або 

1-ій закон Кеплера: кожна із планет рухається по плоскій кривій відносно Сонця так, що радіус-вектор, який зв’язує Сонце і кожну з планет, “замітає” рівні площі за рівні проміжки часу.

2-ій закон Кеплера: траєкторії планет рухаються по еліпсам, в одному з фокусів яких знаходиться Сонце.

З аналізу траєкторій випливає таке твердження:

3-ій закон Кеплера: квадрати періодів обертання планет пропорційні кубам великих осей їх орбіт.

Висновок

Математичне моделювання - метод дослідження процесів або явищ шляхом створення їхніх математичних моделей і дослідження цих моделей.

Математичною моделлю називається сукупність математичних співвідношень, рівнянь, нерівностей, що описують основні закономірності, властиві досліджуваному процесу, об'єкту або системі.

Види моделей:

• динамічні або статичні;
• детерміновані або стохастичні;
• неперервні, дискретні або дискретно-неперервні;
• лінійні чи нелінійні;
• з розподіленими або зосередженими параметрами;
• аналітичні, імітаційні чи комп'ютерні.

Рівняння, яке містить невідому функцію і її похідні, називається диференціальним рівнянням.

Список використанних джерел

1.               https://docviewer.yandex.ua/view/0/?*=GXgzS30EpTBw1QURGxNUFcaOZyN7InVybCI6Imh0dHA6Ly9maWxlcy5raGFkaS5raGFya292LnVhL25hdmNoYWxuaWotdmlkZGlsL2l0ZW0vZG93bmxvYWQvMTEwMTVfZjQ3ODliZmEyZDgyNjIwYzg2ZWQ1YTNkZWI5ODQ5OTYuaHRtbCIsInRpdGxlIjoiMTEwMTVfZjQ3ODliZmEyZDgyNjIwYzg2ZWQ1YTNkZWI5ODQ5OTYuaHRtbCIsInVpZCI6IjAiLCJ5dSI6IjUzNzIwMDcxNTQwMTM5NjkwIiwibm9pZnJhbWUiOnRydWUsInRzIjoxNTQwODEwOTkyODEyLCJzZXJwUGFyYW1zIjoibGFuZz1ydSZuYW1lPTExMDE1X2Y0Nzg5YmZhMmQ4MjYyMGM4NmVkNWEzZGViOTg0OTk2Lmh0bWwmdG09MTU0MDgxMDk3MiZ0bGQ9dWEmdGV4dD0lRDAlOTQlRDAlOTglRDAlQTQlRDAlQTQlRDAlOTUlRDAlQTAlRDAlOTUlRDAlOUQlRDAlQTYlRDAlOTglRDAlOTAlRDAlOUIlRDAlQUMlRDAlOUQlRDAlQUIlRDAlOTUlMjAlRDAlQTMlRDAlQTAlRDAlOTAlRDAlOTIlRDAlOUQlRDAlOTUlRDAlOUQlRDAlOTglRDAlQUYlMjAlRDAlOUElRDAlOTAlRDAlOUElMjAlRDAlOUMlRDAlOTAlRDAlQTIlRDAlOTUlRDAlOUMlRDAlOTAlRDAlQTIlRDAlOTglRDAlQTclRDAlOTUlRDAlQTElRDAlOUElRDAlOTAlRDAlQUYlMjAlRDAlOUMlRDAlOUUlRDAlOTQlRDAlOTUlRDAlOUIlRDAlQUMlMjAlRDAlQTAlRDAlOTUlRDAlOTAlRDAlOUIlRDAlQUMlRDAlOUQlRDAlOUUlRDAlOTMlRDAlOUUlMjAlRDAlOUMlRDAlOTglRDAlQTAlRDAlOTAmdXJsPWh0dHAlM0ElMkYlMkZmaWxlcy5raGFkaS5raGFya292LnVhJTJGbmF2Y2hhbG5pai12aWRkaWwlMkZpdGVtJTJGZG93bmxvYWQlMkYxMTAxNV9mNDc4OWJmYTJkODI2MjBjODZlZDVhM2RlYjk4NDk5Ni5odG1sJmxyPTE0MyZtaW1lPXBkZiZsMTBuPXJ1JnNpZ249Zjk2MzRlNGU3OTcyZGViNGNjYTE2M2ZlYjZlZjg3ZWMma2V5bm89MCJ9&page=4&lang=ru
2.               https://phm.cuspu.edu.ua/images/konf_ftn/2017/s6/Заболотня.pdf
3.               http://stud.wiki/emodel/3c0a65635b2ad79a5d53a89521316d27_0.html
4.               http://works.doklad.ru/view/STe2qxWCq34.html
5.               http://repo.sau.sumy.ua/bitstream/123456789/5782/1/Баталова%20А.%20Б.%20Приклади%20використання.pdf
6.               http://yukhym.com/uk/prikladi-diferentsialnikh-rivnyan/diferentsialni-rivnyannya-osnovni-ponyattya.html
7.               http://diplomba.ru/work/24201