Ділова гра ,,Будівельники'' з теми ,,Площі многокутників''. 8 клас

Методична розробка уроку з предмету ,,Геометрія’’. Ділова гра ,,Будівельник’’ на уроці геометрії у 8 класі.

Тема уроку: Площі многокутників. 

Мета уроку: засвоєння учнями формул для обчислення площ паралелограма, трикутника, трапеції і застосування отриманих знань до розв’язання практичних задач; орієнтація учнів на будівельні професії.

Тип уроку: узагальнення та систематизація знань, умінь і навичок.

                                                    Хід уроку

1.Організаційний момент.

2.Мотивація навчальної діяльності.

Давайте пригадаємо що необхідно вміти для :

• поділу земельних ділянок;
• підрахунку врожаю;
• обклеювання стін шпалерами;
• обкладання кахлем стін;
• фарбування стін, підлоги тощо. (Обчислювати площі геометричних фігур)

Учитель. Пропоную вам подивитися фрагмент відеофільму, в якому представники будівельної галузі, використовують сучасні технології в роботі. Але без математичних знань їм, звичайно, не обійтись. Зокрема в обчисленні площ необхідних матеріалів. (Учні продивляються відеоматеріал).

3. Оголошення теми і завдань уроку.

Сьогодні  наш урок буде проходити у формі гри і пропоную вам об’єднатися у три команди – майбутні бригади оздоблювальників, кожна з яких має командира-бригадира.

Постановка задачи.  Потрібно виконати роботу по покриттю підлоги в дитячому будинку, що має розміри 5,75×8 м. Паркетні плитки мають форму прямокутних трикутників, паралелограмів і рівнобічних трапецій. Розміри плиток в см вказані на малюнку 1.     

                                                                                                                   50

                                           35                                                 

20                                                       20                                                                                          

                                                                  15                               

                                                                                                            20

          15

Паркет укладається у ряди таким чином, що паралелограми і трапеції чергуються, а трикутників в одному ряді всього два.

Правила гри. Перша бригада - столяри. Їм  потрібно виготовити паркетні плитки вказаних розмірів в такій кількості, щоб після покриття підлоги не залишилося зайвих плиток і кількість трикутних плиток було мінімальним, а пліток у формі паралелограмів  і трапецій – однакова кількість.

Друга бригада – постачальники. Їм потрібно доставити необхідну кількість плиток на будівельний майданчик. Вони розраховують цю кількість.

Третя бригада – паркувальники. Щоб  проконтролювати доставку, потрібно знати, скільки і яких паркетних плиток знадобиться для покриття підлоги.

Одержує перемогу та команда, яка першою виконає вірний розрахунок. Для цього потрібно знати формули для обчислення площ вище вказаних фігур.

4. Актуалізація опорних знань і вмінь учнів. Повторення й аналіз фактів.

Проводиться перевірка готовності бригад. З цією метою кожній команді пропонується декілька питань на повторення теоретичного та практичного матеріалу. Потім вчитель проектує на дошку формули і відповіді на завдання, що виконували учні.  Відповіді учнів оцінюються балами.  Рахунок  записуємо у відповідні листи оцінювання.

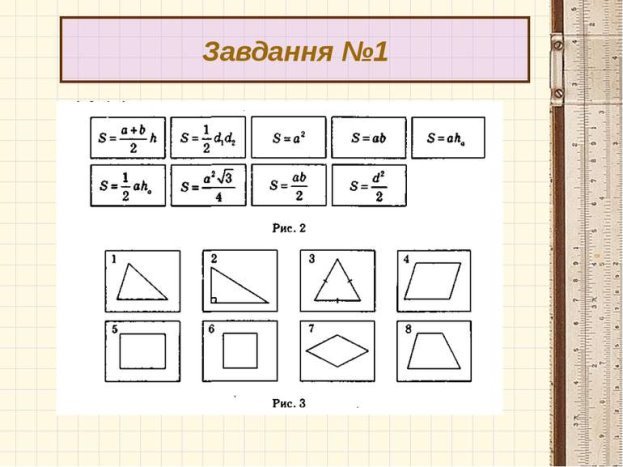
Для  повторення формул, властивостей і площ фігур пропоную вам гру ,,Відшукай’’.

До якої фігури належить дана формула?

             Завдання № 2  Задача практичного характеру.

ЗАДАЧА.  Скільки плиток квадратної форми зі стороною 20 см знадобиться, щоб викласти ними підлогу в кімнаті прямокутної форми, довжина якої 4,6 м,  а ширина 3,4 м?

Розв’язання. Sпр.=4,6*3,4=15.64(м.кв)- площа кімнати

Sкв=0.2*0.2=0.04(м.кв)- площа плитки

n=Sпр:Sкв=15.64:0.04=391(шт.)-кількість плиток

Відповідь: 391 штук.

5.  Удосконалення вмінь і навичок. Практична робота в групах.

Кожна команда приступає до практичних обчислень. Розрахунки показують, що в одному ряді за шириною вкладається по два трикутники і по вісім паралелограмів і трапецій.

Обчислюються площі фігур,  підрахунки. Учні працюють групами і через зазначений час по черзі командир кожної групи демонструє на плакатах результати спільних підрахунків.

           575                              Sпар.під.=575*800 =460 000 -площа підлоги

                                                S1пол=20*575=11500-площа однієї полоси

                                800          n= Sпар.під: S1пол=460 000: 11500=40 полос по

                                                 довжині кімнати. 

                                             Знайдемо кількість паралелограмів і трапецій:

11500-2Sтр=11500-300=11200: (Sтр+Sпар)=11200:1400=8

Sтрик=(20*15):2=300:2=150

Sтр.=((20+50):2)*20=700

Sпар=ah=35*20=700

6. Підсумок  уроку.

Визначення команди-переможця по кількості одержаних балів. Бали високого рівня одержують учні, які  врахували економію матеріалу, особлива увага на математичний зміст роботи і відповіді на контрольні запитання:

1.Дайте визначення площі фігур.

2. За яким принципом укладали паркетні плитки в 1 ряд?

3.Як проводилися обчислення площі одного ряду плиток?

7. Домашнє завдання.

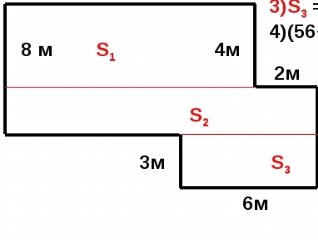
Визначте, скільки потрібно фарби, щоб пофарбувати підлогу, що має форму фігури, що зображена на малюнку, якщо на 1 потрібно 200 г фарби.