Урок з геометрії за темою "Чотирикутники", 8 кл.

Тема уроку: «Чотирикутники»      8 клас

Мета: закріпити отриманні знання по темі «Чотирикутники»; формувати логічне мислення; застосовувати знання при розв’язанні незвичних задач; виховувати корпоративність, вміння швидко приймати правильне рішення; розвиток мовлення.

Хід уроку:

Організаційний момент.

Клас поділити на 3-4 команди по 6-7 чоловік в кожній.

Необхідно підготувати табло для підрахунку балів кожної команди, ігрове поле: на листі ватману накреслено коло, що поділене на сектори, кожен сектор має свій колір; ігровий кубик (його краще зробити великим).

Кожен колір сектора відповідає певному розділу питань, кількість очок – номеру питання по цьому розділу або показує, скільки питань треба пропустити від попереднього (якщо двічі випало одне і те саме число). Команди кидають кубик по черзі, на обміркування питання відводиться одна хвилина. Якщо команда не може відповісти на питання, право відповіді переходить до команди, що раніше інших підняла свій прапорець.

I. Геометрична вікторина

1. Одна з діагоналей ромба дорівнює його стороні. Які кути має ромб?

2. Про опуклий багатокутник відомо, що всі зовнішні кути його тупі. Який це багатокутник?

3. Чи може середня лінія трапеції пройти через точку перетину діагоналей цієї трапеції?

4. Для перевірки того, що вирізаний шматок матерії має форму квадрата, швачка перегинає його по кожній діагоналі і переконується, що краї кожен раз збігаються. Чи достатня така перевірка?

5. Який чотирикутник має лише:

• одну вісь симетрії;

• центр симетрії;

• центр і дві осі симетрії.

6. Квадрат зі стороною 6 см розбили на квадрати зі стороною 2 см. Скільки квадратів вийшло при цьому?

II. Задачі на один зуб

1. Ознака трапеції. Відрізок, який з'єднав середини протилежних сторін опуклого чотирикутника, розділив його площу навпіл. Доведіть, що цей чотирикутник - трапеція.

2. У чотирикутнику АВСD кути В і D прямі, а сторони АВ і ВС рівні. Визначте його площу, якщо відомо, що його висота ВН = 1 см.

3. Піраміда Хеопса має в основі квадрат, а її бічні грані - рівні трикутники. Один єгиптянин лазив нагору і виміряв кут АМD. Вийшло 100. А інший каже, що він перегрівся на сонці, адже такого не може бути. Хто правий?

4. Середина діагоналей трапеції. Довести, що в трапеції відстань між центрами діагоналей дорівнює піврізниці основ.

5. Сума внутрішніх кутів опуклого п-кутника відноситься до суми зовнішніх кутів як 2: 1. Визначити скільки в нього кутів.

6. Властивості ромба. У ромбі одна з діагоналей дорівнює стороні. Знайдіть кути ромба.

ІІІ. Геометрична мозаїка

1.Трапеціі в трикутнику. Як розрізати трикутник на три не прямокутних трапеції.

2.Квадрат з 8 трапецій. Розріжте квадрат на вісім трапецій, серед яких немає прямокутних (запропонуйте два способи).

3.Трикутники в квадраті. Чи можна розрізати квадрат на трикутники так, щоб кожен трикутник межував (по відрізку) рівно з трьома іншими?

4. Як прямокутник слід розрізати на дві такі частини, щоб з них можна було скласти:

- трикутник;

- паралелограм (відмінний від прямокутника);

- трапецію?

5. Є 5 однакових квадратів. Розріжте кожен з них однаковим способом на дві частини і з усіх частин складіть квадрат.

6. Перегинаючи аркуш паперу довільної форми, отримайте зображення прямокутної трапеції, однією з вершин якої є точка А, а інший (протилежної) - точка С.

ІV. Дивимось уважно!

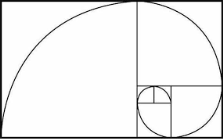
1. Знайдіть сторону квадратів, знаючи, що сторона найменшого квадрата дорівнює 1.

2. Трикутники. Скільки трикутників на цьому малюнку?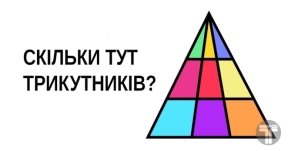

3. Увага! Знайдіть помилку на кресленні.

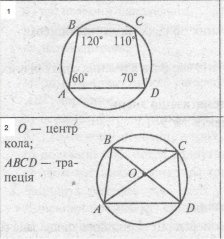
4. В прямокутної трапеції паралельно більшій бічній стороні проведена пряма, яка перетинає більшу основу трапеції в деякій точці. З вершини тупого кута на більшу основу опущений перпендикуляр. Доведіть, що вийшли трикутники рівні один одному.

5. Чи може середня лінія трапеції пройти через точку перетину діагоналей цієї трапеції?

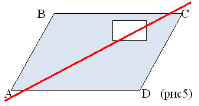
6. На площині дано два пересічних паралелограма. Як провести пряму так, щоб кожен паралелограм розділився нею на рівні частини?

V. Ігри з сірниками

1. Складіть три рівних квадрата з 10 сірників.

2. 16 сірників, 6 квадратів. Перекладіть два сірники із шістнадцяти так, щоб вийшло 6 квадратів.

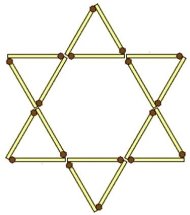
3. Зірка із сірників. Переставте 2 сірники з 18 так, щоб замість 8 трикутників фігура стала складатися з 6 трикутників. Потрібно отримати тільки трикутники і не повинно бути вільно висячих сірників.

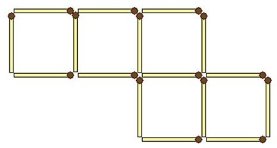
4. Отримайте три квадрати. Перекладіть чотири сірники із шістнадцяти, щоб вийшло три квадрати.

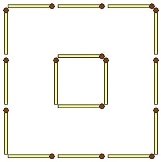
5. Чотири квадрати. Перекладіть три сірники з дванадцяти так, щоб вийшло чотири однакових квадрати з трьох.

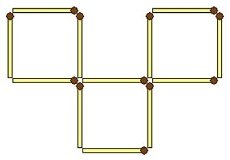
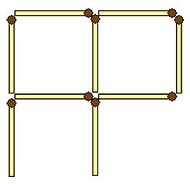
6. Три квадрати. Перекладіть два сірники з дев’яти так, щоб вийшло три квадрати одного розміру.

Підсумки уроку.

Відраховуємо кількість правильно виконаних завдань для кожної команди. Визначаємо переможців. Дякуємо всім за урок. Відмічаємо окремо найактивніших.