Дістанційне навчання

Перехід на дистанційне навчання,обумовлений пандемією, став несподіваним і досить серйозним випробуванням для всіх учасників освітнього  процесу-педагогів,учнів та їх батьків.

Пропонуємо матеріал для самостійного вивчення матеріалу з алгебри 7кл. за оновленим стандартом за підручником  алгебра 7 кл - А.Г.Мерзляк ;

 В.П. Полонський;М.С. Якір Харків «Гімназія» 2020 (2015)

 

 

Тема навчального модуля «Одночлени»

Одночлен. Стандартний вигляд одночлена. Піднесення одночленів до степеня. Множення одночленів

Мета:формування понять одночлена, стандартного вигляду одночлена; формування вмінь учнів множити одночлени та підносити одночлени до степеня, записувати одночлени в стандартному вигляді

Учень/учениця:

наводить приклади:; одночленів

пояснює:одночлен стандартного вигляду, коефіцієнт одночлена,степінь одночлена

формулює: означення: одночлена

розв’язує вправи, що передбачають: зведення одночлена до стандартного вигляду; перетворення добутку одночлена, піднесення одночлена до степеня.

Вивчить:§2  п.7 підручник  алгебра 7 кл - А.Г.Мерзляк ; В.П. Полонський;М.С. Якір Харків «Гімназія» 2020 (2015)

Виконати  вправи по підручнику:№279 (265);285(270);289(272);299(281)

                            Тести  Перевір себе

                                 І рівень

. Оберіть с правильну, на Вашу думку, відповідь.

1. Звести одночлен до стандартного вигляду:    5х ∙ 0,01у ∙ 20.

    а) ху; б) 0,1ху; в) 10ху; г) 100ху.

2. Помножити одночлени:     5ху  і  -7ху.

 а) – 2ху; б) – 35ху; в) – 2ху; г) 35х у.

3.Піднести до квадрата одночлен:     - 0,2 х у.

а) – 0,4ху; б) 0,4ху; в) – 0,04ху; г) 0,04 ху.

4. Виконати піднесення до степеня   ( - 2хуz).

а) – 6xyz; б) - 8xуz; в) – 6xуz; г) – 8хyz.

5. Який з одночленів записаний у стандартному вигляді?
А) – 0,7 b;  Б) 4abb;  В) 3(a²b ³)²;   Г) –8а² ·а.

6. Знайдіть степінь одночлена  (3т³п)² ·3п ³.

А) 11;  Б) 13;  В) 27;   Г) 9.

 

                                 ІІ рівень

Розв’яжіть завдання 7 - 9 та запишіть відповідь

7.Подайте вираз у вигляді одночлена стандартного вигляду

8. Спростити вираз:  

9. Знайдіть значення виразу 5т ²п ³, якщо т = – 0,2, п = –1.

 

                               IІІ рівень

Розв’язання задач 10 -12 повинно мати обґрунтування. У ньому потрібно записати послідовні логічні дії та пояснення, зробити посилання, на математичні факти, з яких випливає те чи інше твердження..

10.  Спростіть вираз і знайдіть його значення.

, якщо  а = –2;   b = –1.

11.. Записати у вигляді одночлена стандартного вигляду ( n – натуральне число ):

    

12.. Знайти значення виразу  - 625ху, якщо  5ху = 4.

 

Тема навчального модуля «Многочлени »

Многочлени. Додавання і віднімання многочленів. Множення одночлена на многочлен, множення многочленів. Розкладання многочлена на множники(винесення спільного множника за дужки,метод групування)

 Учень/учениця:

наводить приклади многочленів в стандартному вигляді

пояснює:многочлен стандартного вигляду,степінь многочлена

формулює: означення: многочлена, подібних членів многочлена степеня многочлена правила: множення одночлена і многочлена, множення двох многочленів

розв’язує вправи, що передбачають: додавання і віднімання многочленів.  зведення подібних членів перетворення добутку одночлена і многочлена, суми, різниці, добутку двох многочленів у многочлен; розкладання многочлена на множники способом винесення спільного множника за дужки, способом групування.

Підручник А.Г.Мерзляк ; В.П. Полонський;М.С. Якір Харків «Гімназія»  2020 (2015)

Вивчити:§2  п.8 і п.9 Виконати вправи по підручнику:№319(295);323(297);34(308);345(311);348(314;)356(322)

 

  тест №2 ст73(64)

Вивчити:§2  п.10

Виконати вправи по підручнику№393(355);395(357);399(361);411(373;)413(375).

Вивчити:§2  п.11

Виконати вправи по підручнику:№432(392);434(394);438(398);440(400);452(412);

Вивчити:§2  п.12

Виконати вправи по підручнику:№480(484);441(489);500(452)

Вивчити:§2  п.13

Виконати вправи по підручнику:№529(476);531(478);536(482);539 (484 )

тест №3 стр. 100(87-88)

Перевір себе Тест №1

І рівень (кожне завдання оцінюється в один бал)

 1.  Многочлен  у² – 8у + 4 + 6у  запишіть у стандартному вигляді.

             а) у² – 2у + 4;        б) у² + 2у + 6;          в) у² – 7у – 6;          г) у² – 8у + 6у + 4.

2.  Знайдіть суму многочленів  2х² + 3х + 6  и  3х² – 2х + 6.

             а)  5х² + х + 12;     б) 5х² – 5х + 12;      в) 5х² – х – 12;        г) х² + 5х – 12.

    3.  Подайте у вигляді многочлена вираз:  –3х (х² – 2х + 1).    

             а) 3х³ + 6х² + 3х;   б) –3х³ + 6х² – 3х;     в) –7х⁴ – 21х³ + 7х;      г) 4х³ – 5х² + 3х.

  4.  Винесіть за дужки спільний множник   9х²у + 5ху² – 6х³.

             а)  х² (9у + 5у² – 6х);                     б)  х (9ху + 5у² – 6х²);

             в)  ху (9х + 5у – 6х);                       г)  х² (9у + 5у² + 6х);

  5.  Запишіть у вигляді добутку  х(а + b) + 2a + 2b.

            а)  (a + b) (x + 2);     б) (a + b) (x + а + b);     в) (2a + 2b) (x + 2);      г) (a + b) (x + 2).

ІІ рівень

 6.  Розв’яжіть рівняння: (х + 6) ^. х = 79 + (х – 5)(х + 5).

 7.  Доведіть, що вираз  2¹² – 2¹⁰ + 2⁹  кратний 56.

ІІІ рівень

 8.  Доведіть, що для будь-якого натурального числа  п  значенні виразу (п + 3) (п + 4) – (п + 1) (п + 6)  ділиться націло на 6.

Правильні відповіді до завдань 1 - 8:

1	2	3	4	5	6	7	8
а	а	б	б	а	9	26 . 56	Доведено

                                         Тест №2

І-рівень

. Оберіть правильну, на Вашу думку, відповідь.

1. Звести до стандартного вигляду многочлен:  5а ∙ 2ав – 3в ∙ 3ав.

    а) 10ав – 9ав; б) 7ав – 6ав; в) - в; г) ав.  

2. Знайти суму многочленів:  5ху – 2х - ху  і  3х - 4ху.

    а) ху + 5х - ху; б) 9ху + х - ху; в) ху + х - ху; г) х.

3. Знайти різницю многочленів:   5х + 3х – х  і  2х – х - х.

   а) 7х - х + 3х – 2х; б) 3х + х + 3х;  в) 3х - х - 3х; г) 3х + х + 3х – 2х.

4. Перетворити добуток у многочлен:   2х(2ху – 3х + у).

    а) 4ху – х + 2ху; б) 4ху – 5х + 2ху; в) 4ху – 6х + 2ху;

 г) 4ху – 6х + 2ху.

5. Виконати множення:   0,2ху(8ху + 5х).

    а) 1,6ху + 5ху; б) 1,6ху + ху; в) 8,2ху + 5,2ху; г) 1,6ху + 0,1ху.

6. Розв’язати рівняння:   3(6х - 3) – 2х = 0. 

    а) коренів немає; б) - ; в) безліч коренів;  г) .

ІІ рівень

Розв’яжіть завдання 7 - 9 та запишіть відповідь.

7. Знайти суму і різницю многочленів:  7х – 2х – 8  і  4х + 3х – 7.

8. Спростити вираз і знайти його значення     3х(3х + 2) – 6(х + 4), якщо х = .

9. Розв’язати рівняння:     5х + = 12 – 2х.

 

IІІ рівень

Розв’язання задач 10 -12 повинно мати обґрунтування.

10. Спростити вираз:    7х(2х – 5) – 5(4х – 3х) – 0,4х.

11. Розв’язати рівняння:    - = .

12. Звести до стандартного вигляду многочлен:

  12х – (7х + 3х – 2(5х - 8)).

 

 

Тема навчального модуля «Формули  скороченого множення»

Добуток різниці та суми двох виразів. Різниця квадратів двох виразів. Квадрат суми та різниці двох виразів. Сума й різниця кубів двох виразів. Застосування різних способів розкладання многочлена на множники.

, Учень/учениця: потрібен вміти: користуватися формулами скороченого множення. до розв'язування практичних задач та раціонального обчислення значень числових виразів

наводить  приклади формул скороченого множення

записує і обґрунтовує: формули скороченого множення

розв’язує вправи, що передбачають: розкладання многочлена на множники за формулами скороченого множення та із застосуванням декількох способів; використання зазначених перетворень у процесі розв’язування рівнянь, доведення тверджень

Підручник А.Г.Мерзляк ; В.П. Полонський;М.С. Якір Харків «Гімназія» 2020(2015)

Вивчити:§2  п.14

Виконати вправи по підручнику:№560(500);561(502);563(504);572(513).

Вивчити:§2  п.15

Виконати вправи по підручнику№596(536;)602(540);612(550).

Вивчити:§2  п.16

Виконати вправи по підручнику:№633(569);639(571);641(573); 648(580).

Вивчити:§2  п.17

Виконати вправи по підручнику:№697(626);699(628);703(632);711(640)

тест№4  129-130 (113-114.)

Вивчити:§2  п.18

 Виконати вправи по підручнику:№752(678);758(679);762(683); 767(68.

Вивчити:§2  п.19

 Виконати вправи по підручнику:№789(707);792(709);802(717);804(719);806(721)

тест №5 ст.145-146(126-127.)

Перевір себе

 

 

 І рівень

 

 

1. Виконайте множення (n – y) (n + y).

a)  n² – 2ny + y²;  б) n² + 2ny + y;

в)  n² –  y²;   г)  n² + y².

 

 

2. Подайте у вигляді многочлена  (x + 4)².

a)  x² – 4x + 16;  б) x² + 8² + 16;

в)  x² – 16;   г) x² – 8x + 16;

 

 

3. Розкладіть на множники многочлен  p² – 25.

а)  (p – 25) (p + 25);               б)  (p – 25) (p – 25);

в)  (p + 5) (p + 5);                    г)  (p – 5) (p + 5).

 

 

 

4. Обчисліть  48² – 38².

a)  860;             б)  10;             в)  86000;            г)  20.

 

 

5. Подайте тричлен  x² – 14x + 49  у вигляді квадрата двочлена:

a)  (x – 7) (x + 7);                     б)  (x + 7)²;

в) (x – 49)²;                               г)  (x – 7)².

 

ІІ рівень

 

 

Спростіть вираз  (0,1a – 0,2b)² + (0,1a – 0,2b) (0,1a + 0,2b)  та знайдіть його значення при a = –50,  .

6. Розв’яжіть рівняння:  2x² – 10x + x² – 25 = 0.

 

 

 

 

ІІІ рівень

 

7. Знайдіть найбільше значення виразу  –9a² + 18a + 45 та значення змінної, при якому вираз набуває найбільшого значення.

 

 

 

 

 

 

 

Правильні відповіді до завдань 1 – 8:

 

1	2	3	4	5	6	7	8
в	б	г	а	г		5;	54, при  а = 1

                                             Тест №2

. Формули скороченого множення 

А	Б	В	Г

1. Подайте у вигляді многочлена вираз:  (с  – 6)².

А	Б	В	Г
с2 - 36	с2 +12с + 36	с2 – 12 с + 36	с2 +36

 

А	Б	В	Г

2.  Подайте у вигляді многочлена вираз:   (5 + c)  (5 – c ).

А	Б	В	Г
25 + с2	с2- 25	5 - с2	25 - с2

 

 

3. Розкладіть на множники:    α²  - 7².        

А	Б	В	Г
(α + 49) (α - 49)	(α + 49) (α - 49)	(α + 7) (α - 7)	(α – 7)2

А	Б	В	Г

 

 

А	Б	В	Г

4. Подайте у вигляді многочлена вираз:   (с² + 5c + 25) (5 -  c) .

А	Б	В	Г
25 – 10с + с2	125 – с3	125 + с3	25 – с3

 

А	Б	В	Г

5. Подайте у вигляді многочлена вираз (α + 3b)(3b – α)                        

А	Б	В	Г
α2  + 9 b2	α2  - 9 b2	9 b2 -  α2	α2- 6αb + 9 b2

 

 

6.  Установіть відповідність між виразами (1– 4) і результатами спрощення цих виразів (А-Д).

	А	Б	В	Г	Д
1
2
3
4

1)   (2 х + у)(у  –2 х)                  А  4 х²  + 8ху + 4у²

2)   (у  –2 х)²                              Б  у² – 4х²

3)    (х + 2у)  (х² – 2ху + у²)      В  х³ +8 у³

4)   (2х + 2у)²                             Г  у² – 4у х + 4х²

   

                                               Д   4х² + 4ху + 4 у²

7..  Спростіть вираз (х – 2)(х + 2) – (х – 5)² .

 

8. Розв’яжіть рівняння  ^:  1) 2х³  - 50х = 0.    2) )  (х – 3)² – (х + 3)² = 24

 

 

Тема навчального  модуля «Функції»

Функції. Способи  завдання функції. Графік функції. Лінійна функція,ії графік і властивості..

, Учень/учениця:

наводить приклади: функціональних залежностей; лінійних функцій

пояснює, що таке: аргумент; функція; область визначення функції; область значень функції; графік функції

формулює означення понять: функція; графік функції; лінійна функція; пряма пропорційність

називає та ілюструє на прикладах способи завдання функції

описує побудову графіка функції, зокрема лінійної та її окремого виду — прямої пропорційності

розв’язує вправи, що передбачають: знаходження області визначення функції; знаходження значення функції за даним значенням аргументу; побудову графіка лінійної функції; знаходження за графіком функції значення функції за даним значенням аргументу і навпаки; визначення окремих характеристик функції за її графіком (додатні значення, від’ємні значення, нулі) потрібен вміти: користуватися формулами скороченого множення. до розв'язування практичних задач та раціонального обчислення значень числових виразів

Підручник А.Г.Мерзляк ; В.П. Полонський;М.С. Якір Харків «Гімназія» 2020(2015)

Вивчити:§3  п.20

 Виконати вправи по підручнику:№851(764);854(767);857(770);864(777); 868(781).

Вивчити:§3 п.21

Виконати вправи по підручнику№879(790);886(792);888(795);891(797);898(803).

Вивчити:§3 

 Виконати вправи по підручнику:№917(821);922(823);923(824);930(829);933(832);937(836).

Вивчити:§3 п.23

 Виконати вправи по підручнику:№954(852);959(854);961(856);968(862);974(868) ; 984(878);991(885);999(893).

тест№6 194-195(170-171).

Перевір себе

Тест №1

І рівень

1. Знайдіть значення функції  y = 2x + 1, якщо значення аргументу дорівнює 5    а) 9;                 б) 11;                 в) 2;                  г) 7.

2. Вкажіть, для якого значення аргументу значення функції y = 8x + 5 дорівнює  -3?

а) 1;                  б) 0;                   в) 10;                г) -1.

3. Яка з вказаних точок належить графіку функції   y = -4x + 2?

а) A (-2; -8);      б) K (-1; 4);      в) B (0; 2);        г) C (1; 10).

4. Функція  y = kx  при x = 4 приймає значення, що дорівнює 26. Знайдіть k.

а) k = 6,5;          б) k = 22;         в) k = -6,5;         г) .

5. При якому значенні k графіки функцій y = kx + 2   и  у = 10 – 5х  паралельні?

а) 5;                   б)  -5;               в)  -10;               г)  .

                                               ІІ рівень

6. Знайдіть координати точки перетину графіків функцій

   y = x – 4    і  ,  якщо вони є.

7. Укажіть найбільше значення функції  y = 3x – 5 на відрізку [-1; 3].

                                               ІІІ рівень

8. Задайте формулою лінійну функцію, графік якої, паралельний прямій y = 3x та проходить через точку А (1; -2). Побудуйте в одній системі координат графіки функцій.

Правильні відповіді до завдань 1 – 8:

1	2	3	4	5	6	7	8
б	г	в	а	б	(14; 10)	4	y = 3x – 5

 

Тест №2

І- рівень

. Оберіть правильну, на Вашу думку, відповідь.

1. Яка з функцій є лінійною функцією:

    а) у = 2х - х; б) у = 2х + 7; в) у  = ; г) у = х – 1 - х?  

2. Функцію задано формулою у = - 0,75х - 2. Знайти значення функції у, якщо

     х = 8.         а) - 6;   б) 6;   в) - 8;   г) 8.

2. Не виконуючи побудови графіка функції у = 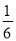х + 3 з’ясувати, чи проходить

      цей графік через точку:       а) (0; - 3); б) (12; 6);  в) (- 12; 1); г) (6; 3).

4. Яка з функцій є прямою пропорційністю:

 а) у = 5; б) у = - х; в) у = - ;     г) у = - 2х + 4?

5. Не виконуючи побудови, знайти нулі функції:   у = - 0,5х + 4. 

    а) 0;    б) 4   ; в) 8  ; г) – 6.

6. Графік якої функції проходить через точку (4; - 6): 

    а) у = 1х; б) у = 3х - 4; в) у = - 1,5х;  г) у = 2х - 2.

ІІ рівень

Розв’яжіть завдання 7 - 9 та запишіть відповідь.

7. Знайти значення k, якщо відомо, що графік функції  у = kх + 5 проходить через     точку А(4; - 7,4).

8. Не виконуючи побудови, знайти координати точок перетину з осями      координат графіка функції:     у = - 0,75х - 21.

9. Побудувати графік функції:  у = х - 3. 

    Знайти: а) нулі функції;     б) значення аргументу, при яких функція набуває додатних значень      в) точки перетину з віссю Оу. 

   

Тема навчального модуля «ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ»

Лінійне рівняння з двома змінними та його графік. Система двох лінійних рівнянь з двома змінними Розв’язування систем двох лінійних рівнянь з двома змінними: графічним способом; способом підстановки; способом додавання

Лінійні рівняння та їх системи як математичні моделі текстових

, Учень/учениця:

Учень/учениця:

наводить приклади: рівняння з однією та двома змінними; лінійних рівнянь з однією та двома змінними; системи двох лінійних рівнянь з двома змінними

пояснює:що таке система двох лінійних рівнянь з двома змінними;скільки розв’язків може мати система двох лінійних рівнянь з двома змінними

формулює означення: лінійних рівнянь з однією та двома змінними; розв’язку рівняння з двома змінними; розв’язку системи двох лінійних рівнянь з двома змінними

будує графіки лінійних рівнянь із двома змінними

описує способи розв’язування системи двох лінійних рівнянь з двома змінними

характеризує випадки, коли система двох лінійних рівнянь з двома змінними має один розв’язок; має безліч розв’язків; не має розв’язків

розв’язує: лінійні рівняння з однією змінною і рівняння, що зводяться до них; текстові задачі за допомогою лінійних рівнянь з однією змінною; системи двох лінійних рівнянь з двома змінними, вказаними у змісті способами; текстові задачі за допомогою систем двох лінійних рівнянь з двома змінними

Підручник А.Г.Мерзляк ; В.П. Полонський;М.С. Якір Харків «Гімназія» 2020 (2015)

7клас Алгебра

Вивчити:§4  п.24

 Виконати вправи по підручнику:№1017(910);1021(914);1034(927).

Вивчити:§4 п.25

  Виконати вправи по підручнику №1060(952);1072(957);1072(96)1;1075(964);1092(98)1;1098(987).

Вивчити:§4  п.26.

  Виконати вправи по підручнику:№1123(1010);1127(1014);1129(1016).

Вивчити:§4 п.27

 Виконати вправи по підручнику:№1148(1034);1150(1036);1153(1038).

Вивчити:§4 п.28

  Виконати вправи по підручнику:№1166(1047);1168(1049);1172(1053).

Вивчити:§4 п.29

 Виконати вправи по підручнику:№1199(1078);1203(1082);1205(1084);1207(1086);1211(1090);1215

(1094);1219(1098);1223(1102);1229(1108) 1241(1120)

 

 

Перевір себе

І рівень

1. Яке рівняння не має коренів?

а)  3х = 5;               б) 0 х = 7;                в)  4 х = 0;         г) -0,4х = 1,3.

2. Коренем якого рівняння буде число 4?

а)  х + 3 = 1;           б) 2х – 10 = -2;        в) 4х – 4(х – 4) = 12;        г) 

3. Розв’яжіть рівняння і знайдіть різницю їх коренів: 0,3х – 1,2 = 0  і  .а) -24,1;                    б) 29;                            в) 21;                            г) 15,6.

4. Які рівняння є рівносильними?

а)       б) х (х + 5) = 0; в) х = 5; г) х² = 25.

5. У двох автобусах їхало 63 пасажири. В другому автобусі їхало в 2 рази більше пасажирів, ніж у першому. Скільки пасажирів їхало в другому автобусі?

а)  43;                  б)  21;  в)  31;  г)  42.

ІІ рівень

6. Розв’яжіть рівняння

7. Зріст Микити 75 см  і ще половина його зросту.  Який зріст Микити?

 

ІІІ рівень

8. Човен за течією річки проплив 2,5 години, а проти течії – 3,6 години. За течією човен проплив відстань на 7,6 км більше, ніж проти течії. Знайдіть швидкість човна за течією, якщо швидкість течії річки –  2 км/год.

 

Правильні відповіді до завдань 1-8.

1	2	3	4	5	6	7	8
б	б	в	а, г	г		1,5 м	км/год

 

Тест№2

Системи лінійних рівнянь з двома змінними»

Виберіть правильний варіант відповіді

1. Яке з наведених рівнянь є лінійним рівнянням з двома змінними?

   а) 3х + 5у = 2;    б) ху = 6;    в) х² – у² = 0;    г) х – 4у² = 1.

2. Скільки розв’язків має рівняння 0  х + 0  у = 0.

   а) один;    б) два;    в) безліч;    г) жодного.

3. Укажіть рисунок, на якому зображено графік функції х + у = 1.

4 Яка пара чисел є розв’язком системи                       

      а) (0; 2); б) (2; 0); в) (0; -2); г) (1; -2).

5. Знайдіть координати точки перетину графіків рівнянь, не виконуючи їх побудови

    х – 2у = 5  і  3х + 5у = 26

6.Скільки розв’язків має система лінійних рівнянь

  а) 1 розв’язок; б) жодного розв’язку; в) 2 розв’язки; г) безліч розв’язків

 

7. На яке число треба помножити обидві частини другого рівняння системи, щоб дістати у рівняннях протилежні коефіцієнти при змінній х:    

      а) -5    ; б) -2;    в) 2;    г) 4.

8. У кошику 46 яблук і груш. Яблук на 12 більше, ніж груш. Яка система

 відповідає умові задачі?

 а)   б)   в) г)

9 За 5 кг апельсинів і 4 кг лимонів заплатили 22 гривні, а за 6 кг апельсинів і 2 кг лимонів – 18 гривень. Скільки коштує 1 кг апельсинів і скільки – 1 кг лимонів?