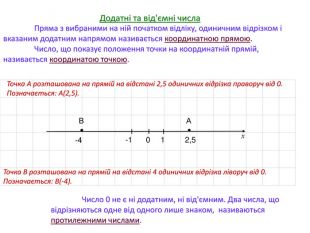
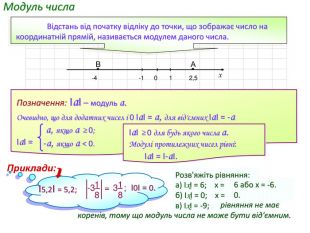
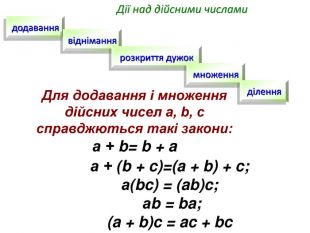
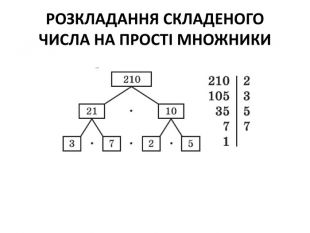
Дійсні числа, порівняння чисел та дії над ними
Про матеріал
Дійсні числа, порівняння чисел та дії над ними
Повторення та пыдготовка до ЗНО Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку