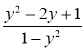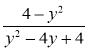Додавання і віднімання дробів з однаковими знаменниками
Тема. Додавання і віднімання дробів з однаковими знаменниками
Мета: домогтися засвоєння учнями змісту правила та алгоритму додавання і віднімання раціональних дробів з однаковими знаменниками та схеми доведення цього правила; сформувати вміння відтворювати вивчені правила та алгоритми, а також виконувати дії відповідно до вивчених правил та алгоритмів для виконання додавання і віднімання раціональних дробів з однаковими знаменниками.
Тип уроку. Засвоєння знань та вмінь
Наочність та обладнання: опорний конспект «Додавання і віднімання дробів».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Самостійна робота № 1 (із наступною перевіркою)
|
Варіант 1 |
Варіант 2 |
|
1. Скоротіть дріб:
а)
г) |
1. Скоротіть дріб:
а)
г) |
|
2. Зведіть дріб:
а)
б)
в) |
2. Зведіть дріб:
а)
б)
в) |
III. Формулювання мети й завдань уроку
З метою свідомої участі учнів у формулюванні мети уроку можна провести бесіду, під час якої запропонувати учням відповісти на такі запитання:
• Які дроби називаються звичайними?
• Які дії зі звичайними дробами ви навчилися виконувати в 6 класі?
• Які дроби називаються раціональними? Чим схожі раціональні дроби на звичайні, а чим вони відрізняються?
• Які дії з раціональними дробами ви навчилися виконувати у 8 класі?
• Чи схожі формули, що виражають алгоритми вивчених дій із раціональними дробами, на відповідні формули для звичайних дробів?
Після закінчення бесіди учні мають усвідомити мету уроку: сформулювати і довести правила додавання і віднімання раціональних дробів з однаковими знаменниками та сформулювати вміння їх застосовувати на практиці.
IV. Актуалізація опорних знань та вмінь
З метою успішного оволодіння учнями навчальним матеріалом уроку перед його вивченням слід активізувати знання і вміння школярів щодо виконання скорочення, додавання та віднімання звичайних дробів; перетворення цілих виразів (додавання і віднімання многочленів, розкладання многочленів на множники), а також скорочення раціональних дробів.
Виконання усних вправ
-
Обчисліть:
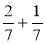 ;
; 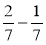 ;
; 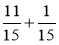 ;
; 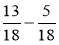 .
.
- Подайте у вигляді добутку:
25 – y2; a2 + ab; 8 + x3; 1 + а2 – 2а; 3х6 – 12х2; b10 – b6.
- Серед виразів знайдіть пари рівних (для зайвого — складіть тотожно рівний вираз):
а) (х + у) – (а + b); б) х + у – а + b; в) х + y – a – b; г) х + у + а – b;
д) (х + у) – (а – b).
V. Засвоєння знань
План вивчення нового матеріалу
- Правило додавання раціональних дробів з однаковими знаменниками та його доведення. Алгоритм виконання додавання раціональних дробів з однаковими знаменниками.
- Правило віднімання раціональних дробів з однаковими знаменниками та його доведення. Алгоритм виконання віднімання раціональних дробів з однаковими знаменниками.
- Приклади застосування складених алгоритмів.
|
Конспект 3 |
|
Додавання і віднімання раціональних дробів |
Для будь-яких А, В, С, де С ≠ 0 правильні рівності:
|
Для будь-яких А, В, С, де С ≠ 0 правильні рівності:
|
Для будь-яких А, В, С і D, де В ≠ 0 і D ≠ 0 правильні рівності:
|
|
Причому BD — найменший спільний знаменник дробів
! Зауваження. Після запису суми (або різниці) раціональних дробів у вигляді дробу необхідно цей дріб скоротити (записувати раціональним дробом залежно від умови завдання) |
Вивчення матеріалу уроку починається із формулювання правила додавання раціональних дробів з однаковими знаменниками у словесній формі та у вигляді тотожності ![]() . Після цього здійснюється доведення складеного правила із використанням властивостей, що були використані під час доведення основної властивості раціонального дробу (див. урок 3, 4).
. Після цього здійснюється доведення складеного правила із використанням властивостей, що були використані під час доведення основної властивості раціонального дробу (див. урок 3, 4).
На підставі доведеного правила далі складається орієнтовна схема дій (алгоритм) під час додавання раціональних дробів з однаковими знаменниками, причому, складаючи алгоритм, бажано звертати увагу учнів як на схожі, так і на відмінні риси алгоритмів додавання і віднімання звичайних та раціональних дробів. (Спільне – правило, відмінне – виконуючи дії додавання чисельників цих дробів, слід користуватися правилом додавання многочленів).
Після закінчення вивчення питання про додавання раціональних дробів з однаковими знаменниками слід розглянути приклади на застосування складеного алгоритму.
Вивчення питання про віднімання раціональних дробів з однаковими знаменниками здійснюється за такою самою схемою, як і додавання раціональних дробів (див. вище).Тому, за умови високого рівня інтелектуальної активності учнів, цей фрагмент уроку можна провести у формі самостійної роботи з вивчення нового матеріалу за готовим планом.
VI. Засвоєння вмінь
Виконання усних вправ
- Перетворіть у дріб вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() .
.
-
Скоротіть дріб: а)
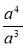 ; б)
; б) 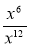 ; в)
; в) 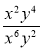 ; г)
; г) 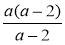 ; д)
; д)  ; є)
; є) 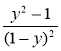 .
.
- Знайдіть допустимі значення змінної у виразах:
х2 – 9; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту.
- Додавання і віднімання раціональних дробів з однаковими знаменниками (на пряме застосування алгоритмів).
1) Виконайте додавання (віднімання) дробів:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) ![]() .
.
2) Спростіть вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
- Перетворення суми або різниці раціональних дробів у раціональний нескоротний дріб (на застосування алгоритмів додавання і віднімання разом з алгоритмом скорочення раціональних дробів).
1) Знайдіть значення виразу:
а) ![]() при b = -3; б)
при b = -3; б) ![]() при а = 0,28.
при а = 0,28.
2) Спростіть вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
- Знаходження значень дробового виразу з попереднім спрощенням його.
Знайдіть значення виразу:
а) ![]() при х = 97; б)
при х = 97; б) ![]() при у = -5,1.
при у = -5,1.
- Виконання вправ на повторення: зведення дробу до нового знаменника, знаходження ОДЗ раціонального дробу, знаходження значень змінних, при яких раціональний дріб дорівнює нулю.
1) Скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) 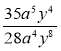 ; є)
; є) 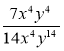 .
.
2) Скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) 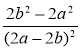 ; г)
; г) 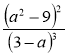 ; д)
; д) ![]() ;
;
є) 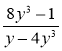 ; ж)
; ж) ![]() ; з)
; з) 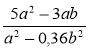 .
.
3) Укажіть область допустимих значень виразу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
- Виконання логічних вправ та завдань підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Спростіть вираз:
а) ![]() ; б)
; б) ![]() .
.
Указівка, а) Многочлен х4 + х2 +1 можна розкласти на множники, записавши його у вигляді (х4 +2х2 + 1) – х2.
|
2) |
Початок дня |
ранок |
|
|
|
? |
Вправи, що пропонуються для розв'язування на цьому уроці, мають сприяти формуванню стійких навичок додавання і віднімання у простих випадках (при цьому відпрацьовується важливий момент: правильний запис суми і найголовніше — різниці чисельників — многочленів поданих дробів у вигляді суми або різниці многочленів із наступним перетворенням записаного виразу в многочлен стандартного вигляду. Підготовча робота проводиться під час виконання усних вправ).
Після успішного опрацювання правил додавання і віднімання у простих випадках учні можуть поступово переходити до сумісного застосування двох правил: правил додавання (віднімання) і скорочення дробів. У більш складній ситуації деякі учні можуть припускатись помилки, що пов'язана зі скороченням дробу на доданок. Тому вже під час розв'язування перших вправ від учнів слід вимагати чіткої послідовності дій:
• перетворити вираз у дріб;
• якщо можливо, розкласти на множники чисельник і знаменник;
• виконати скорочення, якщо в чисельнику і знаменнику дробу с спільні множники.
VII. Підсумки уроку
Чи правильно виконано дії? Знайдіть і виправте помилку.
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() .
.
VIII. Домашнє завдання
- Вивчити правила додавання і віднімання раціональних дробів з однаковими знаменниками (із доведенням для сильних учнів).
- Виконати вправи на застосування вивчених на уроці алгоритмів (рівень складності завдань відповідає рівню складності завдань класної роботи).
- На повторення: вправи на застосування правила знаків (тема «Основна властивість дробу»).

про публікацію авторської розробки
Додати розробку