Формула коренів квадратного рівняння

Тема. Формула коренів квадратного рівняння

Мета: домогтися засвоєння учнями змісту поняття «дискримінант квадратного рівняння з парним другим коефіцієнтом», формули дис­кримінанта квадратного рівняння з парним другим коефіцієнтом та формул коренів такого квадратного рівняння; сформувати первинні вміння знаходити дискримінант квадратного рівняння за новими фор­мулами та за його значенням визначати кількість розв'язків квадрат­ного рівняння, а також обчислювати корені квадратного рівняння; відпрацювати вміння розв'язувати квадратні рівняння за формулами, вивченими на попередньому уроці.

Тип уроку: застосування знань та вмінь.

Наочність та обладнання: Опорний конспект «Квадратні рів­няння».

Хід уроку

I. Організаційний етан

II. Перевірка домашнього завдання

Математичний диктант

III. Формулювання мети і завдань уроку

Усвідомленому вивченню питання уроку (формула коренів квадрат­ного рівняння з парним другим коефіцієнтом) сприятиме поставлене вчителем завдання: за вивченими на попередньому уроці формулами, виконуючи усні обчислення, розв'язати квадратне рівняння з досить ве­ликими коефіцієнтами (рівняння має бути підібране так щоб дискри­мінант був більшим за 10000, тобто не було можливості скористатися таблицею квадратів, наведеною в підручнику). Аналізуючи проблему, доходимо висновку про необхідність «вдосконалення», вивчених на по­передньому уроці формул. Вивчення окремих випадків застосування формул коренів квадратного рівняння та оволодіння вміннями їх вико­ристовувати визначаємо як провідну мету уроку.

IV. Актуалізація опорних знань та вмінь

 Для успішного сприйняття учнями навчального матеріалу уро­ку слід активізувати такі знання і вміння: виконання тотожних перетворень ірраціональних виразів; визначення коефіцієнтів квадратного рівняння; визначення дискримінанта квадратного рівняння та знаходження кількості та значень коренів квадрат­ного рівняння за визначеним значенням дискримінанта.

Виконання усних вправ

1. Укажіть у квадратному рівнянні його коефіцієнти:

а) 3у² – 5у + 1 = 0; б) -х² + х – 3 = 0; в) 12t – 7t² + 4 = 0; г) 9t – 6 + t² = 0;

д) 5т – т² = 0; є) п² – 7 = 0.

2. Спростіть вирази: 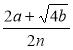; (2k)² – 4ат.
3. Скільки коренів має квадратне рівняння:

x² – 64 = 0; у² + 49 = 0; 2р² – 7р = 0; k² = 0; 2х² + 4х – 1 = 0;

х² + 3х + 4 = 0; у² + 3у + 2= 0.

V. Застосування знань

План вивчення нового матеріалу

1. Формули коренів квадратного рівняння для випадку, якщо другий коефіцієнт рівняння парний.
2. Алгоритм застосування нових формул.
3. Приклад застосування складеного алгоритму.

 У виведенні «нових» формул коренів квадратного рівняння для спрощення виду формул можна відразу ввести додаткові позна­чення: , і під час розв'язування опорних прикладів уже починати закріплення нових позначень. Так само як і на попередньому уроці, після виведення формул слід дати учням орієнтовну схему розв'язання квадратного рівняння цим спосо­бом і в розв'язуванні опорного завдання вимагати строгого її дотримання.

VI. Формування вмінь

Виконання усних вправ

1. Серед даних квадратних рівнянь виберіть ті, в яких парний другий
   коефіцієнт:

a) 3у² – 5у + 1 = 0; б) 12х – 7х² + 4 = 0; в) х² + 2х – 3 = 0; г) 10х² + 3х – 7 = 0.

2. Знайдіть значення виразу 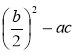якщо:

а) b = -2; а = 3; с = -2; б) b = 6; а = 1; с = 2.

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід розв'язати завдання та­кого змісту:

1. Розв'язування квадратного рівняння за формулами.

1) Розв'яжіть рівняння:

а) х² – 2х – 1 = 0; б) 7х² – 18х + 8 = 0; в) 3х² + 22х – 16 = 0;

г) х² + 21х + 90 = 0; д) 3х² + 53х – 18 = 0; є) -25х² + 50х + 75 = 0;

ж) х² + 0,5х – 1,5 = 0; з) 2х² – х + = 0; и) х² – х – = 0.

2) Розв'яжіть рівняння:
а) 3х² – 14х + 16 = 0; б) 5х² – 16х + 3 = 0; в) х² + 2х – 80 = 0;

г) х² – 22х – 23 = 0; д) 4х² – 36х + 77 = 0; є) 15у² – 22у – 37 = 0;

ж) 7z² – 20z + 14 = 0; з) у² – 10у – 25 = 0.

2. Розв'язування квадратного рівняння найбільш зручним способом.
   Розв'яжіть рівняння:

а) 2х² – 5х – 3 = 0; б) 3х² – 8х + 5 = 0; в) 5х² + 9х + 4 = 0;

г) 36у² – 12y + 1 = 0;  д) 3t² – 3t + 1 = 0; є) х² + 9х – 22 = 0;

ж) у² – 12у + 32 = 0; з) 100х² – 160х + 63 = 0.

3. Розв'язування рівнянь з попереднім виконанням рівносильних пе­ретворень та обранням найбільш зручного способу розв'язання.

1) Розв'яжіть рівняння:

а) t² + 3t = - 4t – 6 – t²; б) 5(y² + 3) = -24у + 20; в) 4х(х – 2) + х² = 6х + 3;

г) 6х² + 3х = 5(2х + 1); д) (х – 1)² + 4х² = 0; е) (3х – 2)(3х + 2) = 6х + 3;

ж) 5х² – х = 0,1 – х + 4х²; з) .

2) Знайдіть корені рівняння:

а) 3(х + 4)² = 10х + 32; б) 15х² + 17 = 15(х + 1)²; в) (x + 1)² = (2х – 1)²;

г) (х – 2)² + 48 = (2 – 3х)².

3) Розв'яжіть рівняння:

а) ; б) ; в) ;

г) .

4) Розв'яжіть рівняння:

а) 0,7х² = 1,3х + 2; б) 7 = 0,4у + 0,2у²; в) х² – 1,6х – 0,36 = 0;

г) z² – 2z + 2,91 = 0; д) 0,2у² – 10y + 125 = 0; є) х² + 2х – 9 = 0.

4. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань. Вставте пропущений вираз.

 Письмові вправи мають на меті закріплення нових формул ко­ренів квадратного рівняння (для рівняння з парним другим коефіцієнтом) та формування вмінь застосовувати ці формули (нові знання) в поєднані з вивченими раніше способами розв'язання квадратних рівнянь. На уроці продовжується за­своєння формул коренів квадратного рівняння, тому, як і на попередньому уроці, з метою попередження помилок та кра­щого запам'ятовування формул, слід вимагати від учнів дотри­мання алгоритму (див. конспект) та усного й письмового відтворення виведених формул.

На цьому уроці можна запропонувати учням завдання, що передба­чає виконання рівносильних перетворень рівнянь перед застосуванням вивчених формул, при цьому слід виділити рівняння, в яких виникає необхідність перетворення рівняння з дробовими коефіцієнтами в рів­няння з цілими коефіцієнтами (множенням обох частин рівняння на НСК знаменників дробових коефіцієнтів) та на рівняння з цілими коефіцієнтами, що мають спільний дільник, відмінний від нуля. Також звертаємо увагу учнів на зручність оволодіння ще й таким прийомом: старший коефіцієнт квадратного рівняння краще мати додатним (в ідеалі - дорівнює одиниці).

VII. Підсумки уроку

В якому випадку правильно знайдено корені?

а) х² – 2х – 8 = 0, D₁ = 1 + 8 = 9, , х₁ = , х₂ = ;

б) х² + 2х – 8 = 0, D₁ = 2 + 8 = 10, ;

в) x² – 4х – 12 = 0, D₁ = 4 + 12 = 16, х_1,2 = 2 ± 4, х₁ = 6, х₂ = -2.

VIII. Домашнє завдання

1. Вивчити всі формули коренів квадратного рівняння.
2. Розв'язати приклади на застосування цих формул.
3. На повторення: тотожні перетворення раціональних виразів та ви­разів, що містять квадратні корені.