Доповідь "Активізація пізнавальної діяльності учнів на уроках математики як засіб підвищення результативності навчального процесу".

Активізація пізнавальної діяльності учнів

на уроках математики як засіб підвищення результативності навчального процесу

Спираючись на досягнення психологіч­ної науки, вчителі досліджують особливості навчання як активної пізнавальної діяльності школярів.

Ця діяльність має спрямовуватися вчителем, а тому він повинен формувати в учнів відповідну мо­тивацію. Якщо не робити цього, то стає цілком ре­альною небезпека, про яку говорив В.О.Сухомлинський: «Усі наші задуми, усі пошуки і побудови зво­дяться нанівець, якщо нема в учня бажання вчити­ся».

Учителі (навіть ті, хто має вже достатній досвід та педагогічну майстерність) перед кожним уроком шукають відповідь на «вічне» запитання: як побуду­вати навчальну роботу, щоб вона викликала емоцій­не піднесення у школярів, неодмінно позитивно впливала на їхні почуття і мислення, збагачувала їх досвідом самостійних пошуків і роздумів. Це дає мож­ливість формувати такі соціально значущі мотиви навчання, як обов'язок перед Батьківщиною, як підго­товку до життя, до суспільно корисної праці, оволо­діння математикою як ключем до пізнання інших наук, практичної діяльності.

У педагогічній практиці давно вже визнано прийо­ми і методи навчання, що допомагають учителеві організувати «навчання із захопленням.

Що ж найцінніше для людини?  «Здоров'я», — не задумуючись відповість кожний. А мені хочеть­ся додати: «Думка». Наскільки дивна захоплююча наука матема­тика. «Математика — це мова плюс міркування, це наче мова й логіка разом. За словами американського фізика Р. Фейнмана, що математика  - це знаряддя для міркування. У ній сконцентровані мислення багатьох людей».

Це відкриття слід донести учням якнайраніше. Ось чому провідна ідея в педагогічній і методичній практиці — максимально розкрити перед учнем спектр застосування математичних знань, передати своє захоплення предметом учням. Саме в цьому аспекті ми ро­зуміємо один із принципів дидак­тики   в   навчанні   математики, а саме: принцип свідомості, актив­ності й самостійності.

Цей принцип полягає в цілеспря­мованому, активному сприйманні явищ, що вивчаються, їх осмис­ленні, творчій переробці й застосу­ванні. Реалізація цього принципу має на меті виконання таких умов:

а) відповідність пізнавальної діяльності учнів закономірнос­тям процесу навчання;

б) пізнавальна активність учнів у процесі навчання;

в) осмислення учнями процесу навчання;

г) оволодіння учнями прийомами розумової діяльності в про­цесі пізнання нового.

Що ж можна розуміти під актив­ністю? Активність є дійовий стан учня, який характеризується прагнен­ням до навчання, напругою і про­явом волі в процесі оволодіння знаннями. Тому активність учнів і називають пізнавальною ак­тивністю. У навчальному процесі активність учнів проявляється не лише в ро­боті думки, а й у практичній діяль­ності, в позакласній — позаурочній роботі, в напруженні волі, а також в емоційних переживаннях.

Розумова активність учнів у про­цесі навчання математики має особливе значення в формуванні понять, осмисленні їх, практич­ному застосуванні й, особливо, в умінні самостійно оперувати цими поняттями. Тому доцільно розглянути методи й форми робо­ти для реалізації цих цілей. В пер­шу чергу це:

1. Груповий метод під час розв'я­зування задач. Робота в парах.
2. Різні форми роботи з книгою.

3. Застосування різних видів за­охочень.
4. Самостійні роботи із застосу­ванням аналогій, порівнянь, карток-інструкцій і консуль­тацій.
5. Використання на уроках еле­ментів історизму, зацікавле­ності (уроки-казки, уроки-подорожі, уроки-кросворди і т. д.).
6. Використання проблемних си­туацій.
7. Виклад матеріалу блоками.
8. Наочність, доступність, оригі­нальність розв'язань різними способами, самостійність в одер­жанні знань, вибір методу роз­в'язування задачі, зв'язок нау­ки з практикою, анкетування, тестування.
9. Спостереження за мовою, рецензіювання за схемою.

Розглянемо деякі конкретні при­клади.

Одним із основних і першочерго­вих завдань у навчанні математи­ки є вироблення в дітей навичок хорошої лічби. Однак одноманітні завдання у вигляді прикладів на обчислення знижують як інтерес до лічби, так і до уроків взагалі. Тому слід мати про запас арсенал різних прийомів, спрямованих на вироблення обчислювальних на­вичок учнів і в той же час не дуже трудомістких для учнів. Це можуть бути блок-схеми (рис. 1), алгоритми, естафети, «Хто швидше запалить вогнище?». (рис. 2)

Виробленню обчислювальних на­вичок сприяє гра «Рибалка»: з чо­тирьох запропонованих на рибках прикладах діти І варіанта «вилов­люють» приклади з відповіддю, наприклад 5, а учні II варіанта — приклади з відповіддю, наприк­лад 6. Наступний вид завдань — кругові приклади, які дозволяють учням здійснювати самокон­троль, а вчителю легко перевіряти роботу учнів. Приклад див. на рис. 3.

Наприклад, у 5 класі під час закріплення вивчених формул ми здійснили «подорож» у «Лісову школу», де звірята не могли роз­в'язати задачі, а діти їм допомог­ли, бо до класу надійшли такі теле­грами:

1. Лисичка задумала загородити город, що має форму прямокутника зі сторонами 10м і 15м. яка довжина огорожі? Допоможіть лисичці.
2. Старенька Сова задумала полетіти в гості до своєї доньки – Совички, яка живе на відстані 26км від неї. Чи долетить вона до доньки за 3 години, якщо летітиме зі швидкістю 8км/год? Допоможіть Сові старенькій.
3. Білочка задумала засіяти квітами клумбу у вигляді квадрата зі стороною 12м. яка площа цієї клумби? Допоможіть білочці.

А ось під час вивчення теми «Масштаб» мотивацію і підхід до теми можна здійснити так. Перед учнями може з’явитися план-схема «підземелля» з коморами. (рис.4) цей шлях можна пройти з Попелюшкою за казкою:

Збирається мачуха з доньками на бал. Попелюшку, звичайно, не беруть, але, щоб видатися «добренькою», мачуха дозволяє Попелюшці по­їхати на бал, якщо ... виконає ма­тематичні завдання, відповіді в яких підкажуть, скільки треба зробити кроків, щоб знайти в підземеллі потрібні комори — завдання. Результат дасть число — код. Постукавши стільки разів у двері, Попелюшка знайде чарів­не слово і ... поїде на бал.

А завдання пропонувались такі:

1. Сума коренів рівнянь 96-х=54, х-49=71, 563+(х-29) = 721   вказує   на кількість коренів від входу до першої комори. (349 кроків)

2.Після того, як від сувою ткани­ни в 97 м відрізали частину, за­лишилося ЗІ м. Скільки ткани­ни відрізали? (66 кроків)

3. У чотирьох коморах було 96 ц зерна. В першу комору добави­ли 26 ц, з другої перенесли в третю 29 ц, а з четвертої ви­тратили 7 ц. Який запас зерна лишився в чотирьох коморах? (115 кроків)

4. Виконай дії за схемою: (І + II + III) - 523 - ?

Попелюшка має одержати слово із 7 букв. (Діти стукають у двері 7 разів і чують кодове слово «Мас­штаб».) А далі йде безпосередня робота над темою «Масштаб» з ви­користанням семантичного, істо­ричного, теоретичного і практич­ного матеріалів.

Під час вивчення теми «Квадратні рівняння» (алгебра, 9 клас) я використовую шифровані завдання такі, наприклад, як

х²+5х-6=0      (-6;1)

у²+10у-24=0    (-12;2)

у²-4у-5=0        (5;-1)

х²+5х-14=0    (-7;2)

х²-8х+15=0    (3;5)

у²-8у+12=0    (2;-6)

Ключове слово «Дружба». Картки-відповіді на рис.5.

Цікавість в учнів викликають зав­дання зі складання листівки у ході обчислень — правильна відпо­відь — правильний кадр листівки.

Кожний учитель не задоволений, якщо бачить на своїх уроках сумні обличчя. Коли ж учні працюють захоплено, то й учитель відчуває задоволення. Уникнути пасив­ності учнів на уроці допомагають командні математичні змагання.

Нехай учням за короткий час слід запам'ятати велику кількість фак­тів. Така ситуація складається, на­приклад, за таблицею множення або за таблицею тригонометричних функцій для кутів 0° 30° ,45⁰, 60°, 90°, за формулами зведення і т. ін.

Пропонуючи запам'ятати той чи інший список, я одночасно оголошую, що наступного уроку опитування за цього матеріалу буде проводитися у вигляді змагання. Правила змагання прості: всі учні розподіляються на команди, від кожної команди до дошки вихо­дить представник, якому команда-суперниця задає по одному за­питанню (коло запитань учням відоме, адже вони вивчали їх вдо­ма). На обдумування відповіді та її записування на дошці дається не більше 5 секунд, і відразу по відповіді оголошується бал-оцінка. Учитель виступає тільки в ролі арбітра: реєстр учасників і їх відповіді, виставляє оцінки, одним словом, — веде протокол змагань.

Коли всі учасники гри закінчують свої виступи, підбивають підсумки, тобто визначається сума балів, на­браних кожною командою. Визна­чається команда-переможниця.

Описане змагання можна поєдну­вати з евристичною бесідою, якщо воно проводиться під час вивчен­ня нового матеріалу.

За кожну правильну відповідь з місця учень одержує жетон, кількість яких підраховується по закінченні уроку. За визначену кількість жетонів учні одержують відповідні оцінки або добавляють бали команді-переможниці.

Така гра примушує учнів уважно слухати пояснення вчителя, за­мислюватися над поставленими запитаннями, шукати на них відповіді, крім того в учителя немає проблем з накопиченням оцінок, й найголовніше — навіть нецікаву і одноманітну на перший погляд роботу, ця гра робить ціка­вою і захоплюючою.

Слід зазначити, що такі нехитрі змагання мобілізують на активну роботу й клас в цілому, й кожного учня зокрема. Бо кожний з них од­ночасно і учасник, і вболівальник. Усім цікаво, наскільки правильно  дасть відповідь на запитання той чи інший учень. При цьому, звичайно, і вболівальник прагне знайти правильну відповідь.

Крім активізації роботи учнів на уроці, такі змагання несуть і вихов­не навантаження: учні співпереживають успіхам своїх товаришів. Члени команди-переможниці ма­ють справу з проблемою справед­ливого розподілу призових балів, і, нарешті, всі просто одержують за­доволення від такого уроку.

Значний арсенал ігор пропонує нам телебачення. Це й різноманітні «шоу», «ринги», «лотереї» тощо.

Традиційні уроки повторення мо­жуть стати засобом активізації творчої діяльності учнів. Це мо­жуть бути уроки-семінари, уроки-бенефіси, уроки-звіти, уроки-консиліуми, уроки однієї теореми, уроки-конференції і т. д.

Так, розглядаючи в 11 класі тему «Геометричний зміст похідної», «Рівняння дотичної до графіка функції», після вступного повто­рення поняття похідної, загальних відомостей для переходу до рівняння дотичної учні са­мостійно працюють з параграфом підручника, шукаючи відповідь на запитання:

1. Означення дотичної до графіка функції f.

2. Чому дорівнює f^'(х)?

3. Дотична — це граничне поло­ження ...
4. У чому полягає геометричний зміст похідної?
5. Як на практиці побудувати до­тичну до  графіка f у точці А(х_0;f(х₀))?

Вдома, читаючи параграф пов­ністю, учні встановлюють, що є Р ще один аспект застосування геометричного тлумачення похід­ної — формула Лагранжа. Це їхнє маленьке відкриття. Зацікавлю­ють учнів і математичні анкети.

Так чи Ні

1.   Чи правильно, що в будь-яку пряму трикутну призму можна вписати циліндр?
2.   Чи   правильно,  що  навколо довільної  прямої трикутної призми  можна  описати  циліндр?
3.   Чи правильно, що в довільний прямокутний паралелепіпед можна вписати циліндр?
4.   Чи правильно, що навколо будь-якого прямокутного па­ралелепіпеда можна описати циліндр?
5.   Чи правильно, що в будь-яку правильну трикутну піраміду можна вписати конус?

Впровадження і традиційних, і нових методів проводиться в поєднанні з широким і комплекс­ним використанням різноманітних дидактичних матері­алів, наочних посібників і технічних засобів навчання. Лише гармонійне поєднання традиційних і нових методів, розуміння суті кожного методу підвищують ефективність уроків з математики.

За час роботи в школі я зібрала певну кількість історико - математичних відомостей, пов'язаних з вивченням шкільного курсу математики, цікавих задач, задач на «кмітливість», старовинних задач, різних математичних «чудес» і використовую їх на уроках.

Під час вивчення теми «Арифметична прогресія» у 9-му класі розв'язуємо історичну задачу про поділ хліба.

Зазвичай, вивчаючи прогресії, розв'язують задачу двохтисячорічної давності про винагороду винахідника шахів. Але значно «старіша» задача — це задача про поділ хліба, яку записано у знаменитому єгипетському папірусі Рінда. Папірус цей, знайдений Ріндом наприкінці минулого сто­ліття, складений близько 2000 років до нашої ери і списа­ний з іншого, ще давнішого математичного твору, який належить, можливо, до третього тисячоліття до нашої ери.

Задача. Сто мір хліба треба поділити між п'ятьма працівниками так, щоб другий одержав на стільки само більше хліба від першого, на скільки третій одержав більше від другого, четвертий більше від третього, п'ятий від четвертого. Крім того, двоє перших повинні одержати хліба у 7 раз менше від трьох інших. Скільки мір хліба треба дати кожному?

Вивчивши формулу суми п перших членів арифме­тичної прогресії, розв'язуємо задачу про поливання городу.

Задача. На городі 30 грядок, кожна — довжиною 16 м і шириною 2,5 м. Поливаючи грядки, городник носить відра з водою з колодязя, розміщеного на відстані 14 м від краю городу, і обходить грядки по межі, причому води, яку він несе за один раз, вистачає для поливання однієї грядки. Якої довжини шлях повинен пройти городник, щоб полити весь город? Шлях почи­нається і закінчується біля колодязя.

Під час вивчення формули суми п перших членів геометричної прогресії, розв'язуємо задачу про яб­лука.

Задача. Садівник продав першому покупцеві по­ловину всіх своїх яблук і ще пів'яблука, другому по­купцеві — половину яблук, що залишилися, і ще пів'яб­лука, третьому — половину яблук, що залишилися, і ще пів'яблука і т.д. Сьомому покупцеві він продав по­ловину яблук, що залишилися, і ще пів'яблука. Після цього яблук у нього не залишилося. Скільки яблук було у садівника?

Розв'язування задач дає можливість пов'язувати викладання математики з життям, виховуючи в учнів активність, самостійність мислення, наполегливість.

Особливо корисні математичні задачі для активі­зації мислення учнів, для збудження їх творчої дум­ки. Саме з задач починається зацікавленість багатьох учнів математикою.

Вивчення теорії і розв'язування задач повинні переплітатися і обумовлювати одне одного. На уро­ках математики навчальний процес іде здебільшого від задач до теорії і потім від теорії до задач.

Вдало дібрана задача допомагає учням усвідоми­ти необхідність оволодіння новими знаннями, які потрібні для розв'язування тієї чи іншої проблеми.

Серед методів навчання, які спрямовані на акти­візацію діяльності учнів, важлива роль належить самостійній роботі.

Практикую короткочасні самостійні роботи з наступним розв'язуванням учнями вправ на дошці й аналізом допущених помилок, напівписьмові робо­ти з використанням дидактичних матеріалів, мате­матичні диктанти, самостійні роботи за підручни­ком. Використовую при цьому колективну, групову та індивідуальну форми роботи.

Підбиваючи підсумки аналізу шляхів активізації навчання учнів на уроках математики, можна зро­бити висновок, що причинами зниження активності учнів, їх аналітичного мислення, причина­ми механічної діяльності учнів є такі закономірності:

1.   Учні отримують однотипні завдання і уроки проводяться одного типу.
2.   Розв'язування задачі зводиться до однієї і тієї ж операції.
3.   Учню не потрібно вибирати результат серед інших, можли­вих у схожих операціях.
4.   Дані задач не є для учня не­звичними.
5.   Він упевнений у безпомилковості   своїх   дій   (задачі   без аналізу).   

В   таких   випадках учень перестає думати, мисли­ти, цікавитися навчальним процесом. Втрачає при цьому і учень, і вчитель.     

ДОДАТКИ

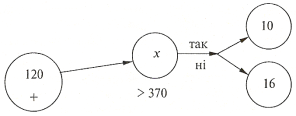
РИС.1

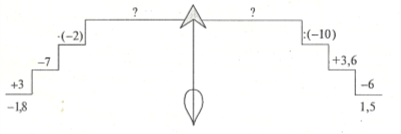
РИС.2.

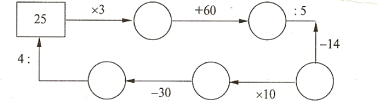
РИС.3

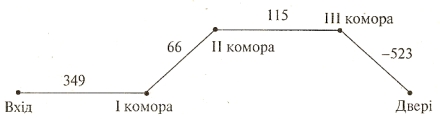
РИС.4

КАРТКИ-ВІДПОВІДІ

РИС.5