Доведення нерівностей в геометрії (для трикутника)
Доведення нерівностей в геометрії (для трикутника)
Доведення нерівностей в геометрії є однією із закритих тем. Таких задач є досить багато у різних розділах, проте на уроках їх розв’язують досить мало.
Задачі на доведення вперше ми зустрічаємо при вивчені теореми Піфагора. Як наслідок з теореми: У прямокутному трикутнику будь-який з катетів менший за гіпотенузу, а тому коли з даної точки до прямої проведені перпендикуляр і похила, то перпендикуляр менший похилої і рівні похилі мають рівні проекції, з двох похилих більша та, у якої проекція більша.
Потім доводимо теорему:
«Які б не були три точки, відстань між будь-якими двома з них не більша за суму відстаней від них до третьої точки». Як наслідок: «У будь-якому трикутнику кожна сторона не більша за суму двох інших сторін». Нерівності трикутника дозволяють доводити великий клас алгебраїчних нерівностей. Наприклад у підручнику «Геометрія, 9 клас, підручник для класів з поглибленим вивченням математики» автори Мерзляк А.Г., Полонський В.Б.. Якір М.С.
Зустрічаємо такі задачі:
-
Знайти найменше значення виразу
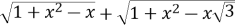 .
.
-
Довести, що для додатних чисел а, b і с виконується нерівність
 .
.
 Розв’яжемо задачу 2.
Розв’яжемо задачу 2.
Побудуємо три довільні відрізки
ОА, ОВ, ОС, такі що АО=а, ОВ=b, ОС= с і ![]() .
.
За теоремою косинусів з трикутників АОВ, ВОС і АОС відповідно маємо:
![]() ,
,
![]()
За нерівністю трикутника, з ![]() АВС випливає очевидна нерівність.
АВС випливає очевидна нерівність. ![]() .
.
Задачі на доведення складають близько 1,4 % від загальної кількості запропонованих задач у підручниках.
При доведенні геометричних нерівностей використовують базові твердження, а саме: нерівність трикутника, обмеженість тригонометричних функцій ![]() та співвідношення між середнім гармонійним, середнім геометричним, середнім арифметичним та середнім квадратичним двох або трьох додатних чисел.
та співвідношення між середнім гармонійним, середнім геометричним, середнім арифметичним та середнім квадратичним двох або трьох додатних чисел.
![]() або
або ![]() .
.
Нерівностей, пов’язаних з тригонометричними функціями кутів трикутника є багато. Доведемо, наприклад, таку:
№1
В довільному трикутнику АВС ![]() .
.
Доведення
Середнє арифметичне і середнє геометричне трьох чисел зв’язані нерівністю ![]() або
або ![]() . Тому
. Тому
![]() (1)
(1)
За умовою А+В+С=π, А+В=π - С.
![]() .
.
![]() .
.
![]()
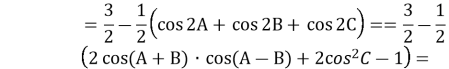
![]()
![]() ;
;
Повернувшись до нерівності (1) одержимо
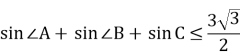
Рівність досягається тоді, коли ![]() .
.
Доведена нерівність має простий геометричний зміст. Помножимо обидві частини нерівності на 2R. Одержимо
![]() , або
, або
![]() ,
, ![]() .
.
Рівність одержимо тоді, коли ![]() , тобто
, тобто ![]() АВС – рівносторонній.
АВС – рівносторонній.
Таким чином з усіх трикутників вписаних у коло, найбільший периметр має рівносторонній трикутник.
№2 Довести, що в довільному трикутнику ![]()
Доведення
Відомо, що в трикутнику ![]()
![]()
![]()
![]() .
.
Але ![]() , тому
, тому
![]() .
.
Знак рівності має місце тоді, коли ![]() .
.
 №3 Довести, що
№3 Довести, що ![]()
Нехай медіани трикутника перетинаються в точці М, а центр описаного кола, точка О.
![]() ,
, ![]() ,
,
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() .
.
Проте ![]() , тому
, тому ![]() ,
,
Проте ![]() .
.
Звідси ![]() (1)
(1)
Використаємо нерівність Коші для трьох чисел ![]()
Виконаємо заміну ![]() .
.
Використавши нерівність (1) одержимо, що
![]() .
.
Рівність одержимо тоді, коли ![]() АВС – рівносторонній.
АВС – рівносторонній.
№4 Довести, що в трикутнику![]() , р – півпериметр.
, р – півпериметр.
 Доведення
Доведення
Нехай АD бісектриса у ![]() АВС.
АВС.
За властивістю бісектриси маємо:
![]() ; або
; або ![]() ,
,
![]() ;
; ![]() ,
,
звідси![]() .
.
Аналогічно виражаємо![]() .
.
Крім того бісектриса
![]() .
.
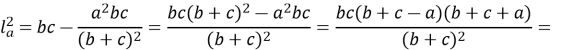
![]() (1)
(1)
Порівняємо ![]()
Складемо різницю
![]() , отже
, отже ![]()
Врахувавши доведену нерівність рівність (1) запишемо у вигляді нерівності
![]()
Рівність досягається тоді, коли трикутник рівносторонній.
Справді ![]() .
.
Тобто бісектриса є одночасно висотою.
№ 5 Довести, що в довільному трикутнику ![]() , де р – півпериметр.
, де р – півпериметр.
Доведення
Для довільних чисел ![]() справедлива нерівність
справедлива нерівність
![]() (1)
(1)
Згідно задачі №4 ![]() ,
, ![]() i
i ![]() ,
,
Тоді ![]()
Знайдений результат підставляємо в нерівність (1).
Одержимо ![]() , або
, або ![]() .
.
Рівність одержимо тоді, коли трикутник рівносторонній.
№6 Довести, що у довільному трикутнику ![]() ,
,
r - радіус вписаного кола.
Доведення
![]()
![]() , тому
, тому ![]() або
або ![]() .
.
Аналогічно ![]() ,
, ![]() .
.
Додамо одержані рівності
![]() . Але
. Але ![]() ,
,
![]() , тому
, тому ![]() . Рівність досягається лише у рівносторонньому трикутнику.
. Рівність досягається лише у рівносторонньому трикутнику.
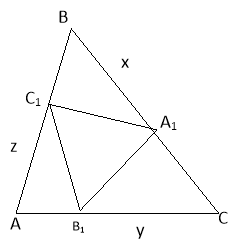
№7 На сторонах АВ, ВС і АС трикутника АВС взяли довільно відповідні точки С1, А1 і В1. Довести, що площа одного з трикутників АВ1С1, А1ВС1, А1В1С не перевищує: а) ![]() ; б)
; б) ![]() .
.
 Доведення
Доведення
а) На сторонах ![]() АВС візьмемо довільні точки А1, В1 і С1.
АВС візьмемо довільні точки А1, В1 і С1.
Введемо позначення, як показано на малюнку,
тоді СА1=а-х, АВ1=в-у, ВС1=с-z.
Знайдемо ![]() ,
,
![]() ;
;
![]() .
.
![]() .
.
Складемо відношення
![]() ;
; ![]() ;
; ![]() .
.
![]() ;
; ![]() ;
; ![]() .
.
Перемножимо рівності
![]() ;
;
Оцінимо
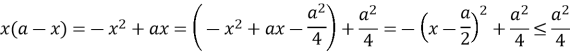
Аналогічно ![]() ;
; ![]() .
.
![]() .
.
Оскільки добуток трьох множників не більший від ![]() , то обов’язково один із множників не більший
, то обов’язково один із множників не більший ![]() . Рівність досягається тоді, коли точки А1, В1 і С1 – середини сторін.
. Рівність досягається тоді, коли точки А1, В1 і С1 – середини сторін.
б) У випадку а)![]()
![]()
![]() ; (1)
; (1)
Позначимо ![]()
![]()
![]() , тоді
, тоді
![]() .
.
Виконаємо заміну у рівність (1).
![]() .
.
Нехай ![]() , тоді
, тоді ![]() (див. випадок а)
(див. випадок а)
(0<m<1) ![]() , або
, або ![]() .
.
З’ясуємо, якого значення набуває вираз ![]() .
.
Нехай ![]() , тоді
, тоді ![]() ;
; ![]() при
при ![]()

![]() ,
, ![]() .
.
При ![]() ,
, ![]() , це може бути як один з випадків, коли А1, В1 і С1 – середини сторін трикутника АВС.
, це може бути як один з випадків, коли А1, В1 і С1 – середини сторін трикутника АВС.
Отже ![]() , тому відношення
, тому відношення ![]() буде завжди менше від числа, яке не менше
буде завжди менше від числа, яке не менше ![]() .
. ![]() в допустимих межах.
в допустимих межах.
У випадку а) існує трикутник ![]() , який не більше
, який не більше ![]() , тому
, тому ![]() не більший за
не більший за ![]() . Рівність одержимо тоді, коли точки А1, В1 і С1 є серединами сторін трикутника.
. Рівність одержимо тоді, коли точки А1, В1 і С1 є серединами сторін трикутника.
№8 Довести, що у прямокутному трикутнику має місце нерівність ![]() ,де h – висота проведена до гіпотенузи, r - радіус вписаного кола.
,де h – висота проведена до гіпотенузи, r - радіус вписаного кола.
Доведення
а) Нехай ![]() , тоді
, тоді ![]() .
.
Відомо, що S=pr, ![]() .
.
Звідси ![]() , тому
, тому ![]() .
.
б) ![]() , звідси
, звідси ![]() (1)
(1)
Проте
![]()
Використавши нерівність ![]() з рівності (1) одержимо
з рівності (1) одержимо
![]() .
.
№9. Довести, що площа рівнобедреного трикутника не більша ![]() квадрата медіани, проведеної до бічної сторони.
квадрата медіани, проведеної до бічної сторони.
Доведення
 а) Нехай АВ – основа рівнобедреного трикутника АВС, AD – медіана, проведена до бічної сторони. Проведемо DK
а) Нехай АВ – основа рівнобедреного трикутника АВС, AD – медіана, проведена до бічної сторони. Проведемо DK![]() AB. Введемо позначення: AD=m, AK = x, DK = y.
AB. Введемо позначення: AD=m, AK = x, DK = y.
S - площа ![]() АВС.
АВС.
АК:КВ=3:1, тоді АВ=![]() ,
, ![]() .
.
Оскільки ![]() , то
, то ![]() ,тоді
,тоді ![]() . Рівність досягається, коли х=у.
. Рівність досягається, коли х=у.
б) Нехай ![]() , тоді з
, тоді з ![]() .
.
![]() .
.
Отже ![]() . Рівність досягається, якщо
. Рівність досягається, якщо ![]() .
.
в) Нехай кут між медіанами AD і BE дорівнює ![]() .
.
Площа трапеції ABDE ![]() , тому площа трапеції становить
, тому площа трапеції становить ![]() площі
площі ![]() АВС.
АВС.
![]() .
.
Отже ![]() . Рівність досягається, якщо
. Рівність досягається, якщо ![]() .
.
Задачі для самостійної роботи
№1. Довести, що в довільному трикутнику:
-
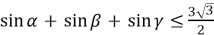 .
.
-
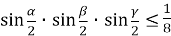 .
.
-
Сума медіан більша
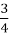 периметра, але менше периметра.
периметра, але менше периметра.
-
 , де r - радіус вписаного кола,
, де r - радіус вписаного кола, 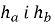 висоти.
висоти.
-
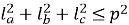 , де р – півпериметр,
, де р – півпериметр, 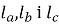 - бісектриси.
- бісектриси.
-
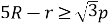 , де R – радіус описаного кола, r - радіус вписаного кола, р - півпериметр.
, де R – радіус описаного кола, r - радіус вписаного кола, р - півпериметр.
-
 .
.
№2 Довести, що у нетупокутному трикутнику ![]() ,
, ![]() - відповідні медіани, R – радіус описаного кола.
- відповідні медіани, R – радіус описаного кола.


про публікацію авторської розробки
Додати розробку
