Довідковий матеріал до теми "Елементарні геометричні фігури та їх властивості" і теми "Взаємне розміщення прямих на площині"

ГЕОМЕТРІЯ, 7          ТЕМА 1. ЕЛЕМЕНТАРНІ ГЕОМЕТРИЧНІ ФІГУРИ ТА ЇХ ВЛАСТИВОСТІ

Аксіома I                           Аксіома II  Аксіома III

Ba, Ca                               одна пряма АВ                   С лежить між А і В

Відрізком називають частину прямої, яка складається з усіх точок цієї прямої,
що лежать між двома її точками, разом із цими точками. Ці точки - кінці відрізка.

Аксіома IV.  Кожний відрізок має певну довжину, більшу за нуль.            AB > 0

Аксіома V.  Якщо C  AB, то AC + CB = AB

                       Кут - це геометрична фігура, яка складається з двох променів, що виходять з однієї точки.

Аксіома VI.  Кожний кут має певну градусну міру, більшу за нуль. Розгорнутий кут дорівнює 180°. Аксіома VII. Промінь OK проходить між сторонами кута AOB.                   AOK + KOB = AOB.

                       Бісектрисою кута називають промінь, який виходить з його вершини і ділить кут навпіл.

ГЕОМЕТРІЯ, 7          ТЕМА 2. ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЯМИХ НА ПЛОЩИНІ

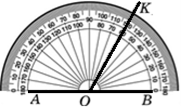Означення. Два кути називають суміжними, якщо одна сторона в них є спільною, а дві інші сторони цих кутів є доповняльними променями.

Властивість суміжних кутів.           AOK + KOB = 180°

Наслідок 1. Кут, суміжний з прямим кутом, — прямий.

Наслідок 2. Кут, суміжний з гострим кутом, — тупий, а
                      кут суміжний з тупим кутом, — гострий.

Означення. Два кути називають вертикальними, якщо сторони одного кута є доповняльними променями сторін другого.

Властивість вертикальних кутів. 1 = 2, 3 = 4.

Менший з вертикальних кутів називають кутом між прямими.

Паралельні прямі

Означення. Дві прямі на площині називають паралельними, якщо вони не перетинаються.

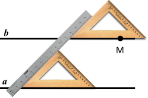Аксіома VIII. Через точку, що не лежить на даній прямій, можна
                         провести тільки одну пряму, паралельну даній. a || b.

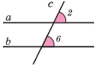
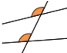
Означення. Пряма c називається січною для прямих a і b, якщо вона перетинає їх у двох точках.

Ознака паралельності прямих

Якщо при перетині двох прямих січною відповідні кути рівні, то прямі паралельні.

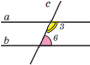
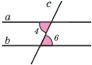Наслідок 1. Якщо при перетині двох прямих січною внутрішні різносторонні кути рівні, то прямі паралельні.

Наслідок 2. Якщо при перетині двох прямих січною сума внутрішніх односторонніх кутів дорівнює 180°, то прямі паралельні.

Властивості паралельних прямих: відповідні кути і внутрішні різносторонні кути рівні, а сума внутрішніх односторонніх кутів дорівнює 180°; дві прямі, паралельні третій, паралельні.

Перпендикулярні прямі

Означення. Дві прямі називають перпендикулярними, якщо вони перетинаються під прямим кутом.

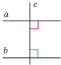
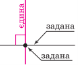                              Властивості перпендикулярних прямих

1.Через кожну точку прямої проходить                   2. Якщо ca і a||b, тоді cb.

лише одна пряма, перпендикулярна до даної.     

Відрізки, промені називають перпендикулярними, якщо вони лежать на перпендикулярних прямих.

Перпендикуляр

Означення. Перпендикуляром до даної прямої називають відрізок прямої, перпендикулярної
до даної, один із кінців якого лежить на даній прямій.

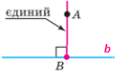
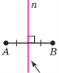
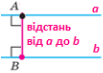
                АВ  b              Основа перпендикуляра     Серединний перпендикуляр до відрізка АВ.

Означення. Довжину перпендикуляра АВ називають відстанню від точки А до прямої b.