Довідковий матеріал з теми «Ознаки подільності»

Довідковий матеріал

з теми

«Ознаки подільності»

(математика, 6 клас)

 

I.Кратні числа

 

Кратним натуральному числу а називають натуральне число, яке ділиться на а без остачі.

Приклади:

а) для числа 18 кратними є числа: 18, 36, 54, 72, 90, 108, 126 і т.д.;

б) для числа 7 кратними є числа: 7, 14, 21, 28, 35, 42, 49 і т.д.

Отже, треба запам'ятати:

1) будь-яке число має нескінченну кількість кратних;

2) найменшим кратним для числа є саме це число.

 

II.Дільники числа

Дільником натурального числа а називається натуральне число, на яке а ділиться без остачі.

Приклади:

а) число 18 має шість дільників: 1, 2, 3, 6, 9, 18;

б) число 25 має 3 дільники: 1, 5, 25;

в) число 73 має 2 дільники: 1 і 73.

Число 1 є дільником будь-якого натурального числа.

 

Поглиблення знань

Число, яке дорівнює сумі своїх дільників, не враховуючи самого числа, називається досконалим числом.

Наприклад, 6=1+2+3; 28=1+2+4+7+14.

Дружніми числами називають два натуральні числа такі, що сума всіх дільників першого (за винятком самого числа) рівна другому числу, а сума всіх дільників другого числа (за винятком самого числа) рівна першому числу.

Наприклад для 220 такими дільниками є числа 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 і 110 сума яких рівна 284, а для 284 дільниками є 1, 2, 4, 71, і 142 сума яких рівна 220. Отже (220,284) є парою дружніх чисел.

Найменшими парами дружніх чисел є (220, 284), (1184, 1210), (2620, 2924) (5020, 5564), (6232, 6368), (10744, 10856), (12285, 14595), (17296, 18416), (63020, 76084).

 

III.Ознаки подільності на 2, 3, 5, 9, 10

Цифри 0, 2, 4, 6, 8 називають парними, а цифри 1, 3, 5, 7, 9 - непарними.

Натуральні числа називають парними, якщо вони закінчуються парною цифрою, і непарними, якщо вони закінчуються непарною цифрою.

Правило: Якщо запис натурального числа закінчується парною цифрою, то це число ділиться без остачі на 2, а якщо непарною цифрою - то число не ділиться без остачі на 2.

Приклади:

а) 8, 60, 574 - діляться на 2;

б) 13, 25, 1001 - не діляться на 2.

Правило: Якщо запис натурального числа закінчується на 0, то це число ділиться без остачі на 10.

Якщо запис натурального числа закінчується будь-якою іншою цифрою, то воно не ділиться без остачі на 10.

Приклади:

а) 680 ділиться на 10;

б) 104 не ділиться на 10.

Правило: Якщо запис натурального числа закінчується цифрами 0 або 5, то це число ділиться без остачі на 5.

Якщо запис числа закінчується будь-якою іншою цифрою, то число не ділиться на 5 без остачі.

Приклади:

а) 370 і 1485 діляться без остачі на 5;

б) числа 537 і 4008 без остачі на 5 не діляться.

Правило: Якщо сума цифр числа ділиться на 3, то й число ділиться на 3. Якщо сума цифр числа не ділиться на 3, то й число не ділиться на 3.

Приклади:

а) 276 ділиться на 3, оскільки 2 + 7 + 6 = 15, а 15 ділиться на 3;

б) 563 не ділиться на 3, оскільки 5 + 6 + 3 = 14, а 14 не ділиться на 3.

Правило: Якщо сума цифр числа ділиться на 9, то й саме число ділиться на 9. Якщо сума цифр числа не ділиться на 9, то й число не ділиться на 9.

Приклади:

а) 5787 ділиться на 9, оскільки 5 + 7 + 8 + 7 = 27, а 27 ділиться на 9;

б) 359 не ділиться на 9, оскільки 3 + 5 + 9 = 17, а 17 не ділиться на 9.

Отже, треба запам'ятати:

1) нуль ділиться на будь –яке натуральне число;

2) будь –яке натуральне число ділиться на 1;

3) якщо кожний доданок ділиться на деяке число, то і сума ділиться на це число;

4) якщо в добутку хоча б один із множників ділиться на деяке число, то і добуток ділиться на це число.

 

Поглиблення знань

Правило: Число ділиться на 4, якщо число, складене із двох останніх цифр даного числа, ділиться на 4.

Приклади:

а) 78 536 ділиться на 4, оскільки 36 ділиться на 4;

б) 8422 не ділиться на 4, оскільки 22 не ділиться на 4.

Правило: Число ділиться на 6, якщо воно одночасно ділиться на 2 і на 3.

Приклади:

а) 2862 ділиться на 6, оскільки 2862 ділиться і на 2, і на 3;

б) 3754 не ділиться на 6, оскільки 3754 не ділиться на 3.

IV.Прості та складені числа

Натуральне число називають простим, якщо воно має лише два дільники: одиницю і саме число.

Натуральне число називають складеним, якщо воно має більше двох дільників.

Приклади:

а) число 9 має три дільники (1, 3 і 9), значить, воно складене;

б) число 17 має два дільники, значить, воно просте;

в) число 1 має лише один дільник - саме це число, тому воно не є ні простим, ні складеним.

Правило: Розкласти складене число на прості множники означає записати дане число у вигляді добутку простих чисел - дільників даного числа.

При будь-якому способі запису одержуємо один і той самий розклад, якщо не враховувати порядку розміщення множників.

Приклади:

а) 180 = 2 · 2 · 3 · 3 · 5;

б) 1368 = 2 · 2 · 2 · 3 · 3 · 19.

 

 

 

Поглиблення знань

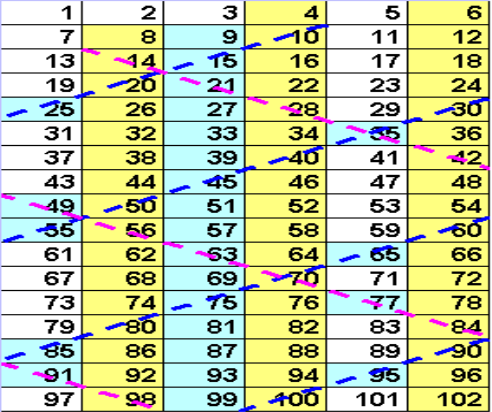
Решето Ератосфена

Історія математики знає імена вчених, які чимало працювали над складанням таблиць простих чисел. Перші такі спроби робилися ще у Стародавній Греції.

Для знаходження простих чисел давньогрецький учений Ератосфен (бл. 276 - бл. 194 р. до н. е.) запропонував певний спосіб. Він виписував усі числа від 1 до якогось числа а. Викреслював число 1, яке не є простим. Підкреслював число 2 і викреслював усі числа, які діляться на 2, тобто числа 4, 6, 8, ... . Наступне незакреслене число 3 є простим. Ератосфен підкреслював це число і викреслював усі числа, які діляться на 3. Підкреслював наступне невикреслене число 5, яке є простим, і т. д. У такий спосіб серед чисел, що не перевищують а, можна «висіяти» всі прості числа.

Якщо «висіяти» всі прості числа, що не перевищують 30, то одержимо: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 — перші 10 простих чисел.

 Метод Ератосфена «висіювання» простих чисел називають ще «решетом Ератосфена». Це пов'язано з тим, що давні греки писали на папірусах або табличках, покритих воском, і числа не викреслювали, а виколювали голкою, після чого папірус або табличка нагадували решето.

 

 

V.Найбільший спільний дільник (НСД)

Найбільше натуральне число, на яке діляться без остачі числа а і b, називається найбільшим спільним дільником (НСД) цих чисел.

Правило: Щоб знайти найбільший спільний дільник декількох натуральних чисел, потрібно:

1) розкласти дані числа на прості множники;

2) виписати ті спільні множники, які є в розкладі кожного із чисел,

3) знайти добуток цих множників.

Приклади:

а) Знайти НСД (6600; 6300):

6600 = 2 · 2 · 2 · 3 · 5 · 5 · 11,

6300 = 2 · 2 · 3 · 3 · 5 · 5 · 7,

НСД (6600; 6300) = 2 · 2 · 3 · 5 · 5 = 300.

Натуральні числа називають взаємно простими, якщо їх найбільший спільний дільник дорівнює одиниці.

Приклади:

а) 75 і 14 - взаємно прості числа, оскільки НСД (75; 14) = 1;

б) 20, 9 і 77 взаємно прості числа, оскільки НСД (20; 9; 77) = 1.

 

Поглиблення знань

При знаходженні найбільшого спільного дільника двох чисел корисно знати ще одне правило, яке називається «алгоритмом Евкліда».

Алгоритм Евкліда:

Щоб знайти НСД двох натуральних чисел, треба спочатку більше число розділити на менше, потім менше число ділимо на остачу від ділення, а потім остачу від першого ділення ділимо на остачу від ділення другого і т. д. Остання в цьому процесі остача, яка не дорівнює нулю, і буде НСД даних чисел.

Приклад: Знайти НСД (270; 186). Поділимо 270 на 186 з остачею:

270 : 186 = 1 (ост. 84).

Потім поділимо дільник на остачу і т.д.:

186 : 84 = 2 (ост. 18),

84 : 18 = 4 (ост. 12),

18 : 12 = 1 (ост. 6),

12 : 6 = 2 (ост. 0).

Найбільшим спільним дільником чисел 270 і 186 є остання, відмінна від нуля остача, тобто число 6.

Приклад: Знайти НСД (234; 180).

1) 234 : 180 = 1 (ост. 54),

2) 180 : 54 = 3 (ост. 18),

3) 54 : 18 = 3 (ост. 0).

Значить, НСД (234; 180) = 18.

 

VI.Найменший спільний кратний (НСК)

Найменшим спільним кратним (НСК) натуральних чисел а і b називають найменше натуральне число, яке кратне і а, і b.

Треба запам'ятати: 

1) якщо одне із двох натуральних чисел ділиться на друге число, то більше з цих двох чисел є їх найменшим спільним кратним;

2) якщо два числа є взаємно простими, то найменше спільне кратне цих чисел дорівнює їх добутку.

Приклади:

а) НСК (9; 18) = 18;

б) НСК (2; 8; 16) = 16, оскільки 8 ділиться на 2, а 16 ділиться на 8;

в) НСК (7; 10) = 70, оскільки 7 і 10 - взаємно прості числа.

У деяких випадках найменше кратне двох чисел знаходять усно.

Приклади:

а) НСК (12; 18) = 36;

б) НСК (18; 30) = 90;

в) НСК (5; 10; 12) = 60;

г) НСК (14; 8) = 56.

Правило: Щоб знайти найменше спільне кратне декількох натуральних чисел, треба:

1) розкласти їх на прості множники;

2) виписати множники, що входять у розклад (краще найдовший) одного з чисел;

3) дописати до них ті множники, що є в розкладі інших чисел;

4) знайти значення утвореного добутку.

Приклад: Знайдемо найменше спільне кратне чисел 360 і 825, користуючись цим правилом.

1) 360 = 2 · 2 · 2 · 3 · 3 · 5,

825 = 3 · 5 · 5 · 11;

2) випишемо найдовший розклад:

2 · 2 · 2 · 3 · 3 · 5;

3) допишемо до нього множники з другого розкладу, яких не вистачає: 5 і 11;

4) НСК (360; 825) = 2 · 2 · 2 · 3 · 3 · 5 · 11 = 19 800.