Довідник з математики: для підготовки до ЗНО та НМТ: Означення, формули, теореми

Про матеріал

Довідник складено на основі програми з математики для загальноосвітніх навчальних закладів, а також Державного стандарту базової і повної загальної середньої освіти України. Його мета – допомогти учням старших класів самостійно повторити й систематизувати знання з елементарної математики під час підготовки до ЗНО.та НМТ.

Перегляд файлу

Середня загальноосвітня школа № 13 м. Львова

ГАЛИНА ВАСИЛЬКІВ

ДОВІДНИК З МАТЕМАТИКИ

ДЛЯ ПІДГОТОВКИ ДО ЗНО ТА НМТ

Означення, формули, теореми

Львів – 2022

Васильків Г. І.

Довідник з математики: для підготовки до ЗНО та НМТ: Означення, формули, теореми. – Львів, 2022. – 60 с.

У посібнику подано основні означення, формули й теореми., указано деякі методи розв’язування рівнянь і нерівностей та їх систем. Не слід думати, що цей короткий довідник покликаний замінити шкільні підручники. Його мета – допомогти учням старших класів самостійно повторити й систематизувати знання з елементарної математики під час підготовки до ЗНО.та НМТ Довідник буде корисним для вступників до вищих навчальних закладів, слухачів підготовчих курсів, учнів загальноосвітніх шкіл, гімназій і ліцеїв.

ЗМІСТ

Передмова .......................................................... 4

§ 1. Перетворення алгебричних виразів................................ 5

§ 2. Перетворення логарифмічно-показникових виразів 8

§ 3. Перетворення тригонометричних виразів..................... 10

§ 4. Алгебричні рівняння та нерівності............................... 17

§ 5. Ірраціональні рівняння та нерівності............................ 19

§ 6. Показникові рівняння та нерівності.............................. 21

§ 7. Логарифмічні рівняння та нерівності............................ 22

§ 8. Рівняння та нерівності з модулями............................... 24

§ 9. Тригонометричні рівняння та нерівності...................... 25

§ 10. Системи рівнянь та нерівностей................................. 26

§ 11. Похідна функції та її застосування............................. 27

§ 12. Первісна та інтеграл................................................... 29

§ 13. Прогресії..................................................................... 31

§ 14. Відсотки..................................................................... 32

§ 15. Планіметрія................................................................ 34

§ 16. Стереометрія............................................................... 43

§ 17. Вектори....................................................................... 52

§ 18. Елементи комбінаторики. ............................................

Початки теорії ймовірностей 54

Література ......................................................... 60 ПЕРЕДМОВА

Матеріал книжки охоплює всі розділи, передбачені програмою з математики для середньої школи.

Кожен параграф містить стислий виклад основних теоретичних відомостей – означень, формул і теорем.

Основна мета довідника – активізувати повторення й систематизацію вивченого матеріалу.

Довідник складено на основі Державного стандарту базової і повної загальної середньої освіти. Він буде корисним для вступників до вищих навчальних закладів України, а також для слухачів підготовчих курсів, учнів загальноосвітніх шкіл, гімназій і ліцеїв.

§ 1. Перетворення алгебричних виразів

Числа 1, 2, 3, ..., які використовуються у лічбі, утворюють множину натуральних чисел. Цю множину позначають літерою N . Натуральні числа, протилежні їм числа та число нуль складають множину цілих чисел. Множину цілих чисел позначають літерою Z .

Числа, які можна подати у вигляді дробу , де m – ціле n

число, а n – натуральне, називають раціональними. Множину раціональних чисел позначають літерою Q . Кожне раціональне число можна подати у вигляді нескінченного десяткового періодичного дробу. Наприклад:  0,333... 0,(3) ,  0,1(6) і под. Деякі раціональні числа можна подати у вигляді нескінченного десяткового дробу двома різними способами, наприклад  0,5000...  0,4999... . Щоб уникнути такої неоднозначності, у цих випадках зазвичай беруть десятковий дріб зі скінченною кількістю значущих цифр і нескінченною кількістю нулів. Нескінченні десяткові неперіодичні дроби утворюють множину ірраціональних чисел. Наприклад, числа 3,1415926..., e2,7182812..., 2 1,4142135... – ірраціональні.

Множина дійсних чисел складається з множин раціональних та ірраціональних чисел. Множину дійсних чисел позначають літерою R .

Алгебричним виразом називається вираз, в якому над числами і змінними скінченне число разів здійснюються алгебричні операції: додавання, віднімання, множення, ділення, піднесення до цілочислового степеня і добування кореня.

Якщо алгебричний вираз не містить ділення на змінні і добування кореня зі змінних, то він називається цілим раціональним виразом (многочленом).

Якщо алгебричний вираз не містить добування кореня зі змінних, але містить ділення на вираз зі змінними, то він називається дробово-раціональним виразом.

Формули скороченого множення

(a  b)²  a²  2ab  b² ; (1.1)

(a b)²  a²  2ab  b²; (1.2)

(a  b)³  a³  3a²b  3ab²  b³ ; (1.3) (a b)³  a³ 3a²b  3ab² b³; (1.4) a² b²  (a b)(a  b) ; (1.5) a³ b³  (a  b)(a²  ab  b²); (1.6)

aⁿ bⁿ  (a b)(aⁿ^1  aⁿ^2b  aⁿ^3b² ... abⁿ^2 bⁿ^1); (1.6а)

a³  b³  (a  b)(a²  ab  b²) ; (1.7)

a  b  c²  a²  b²  c²  2ab  2ac  2bc . (1.8)

Степені та їхні властивості 1

aⁿ  a14a2...43a; aⁿ  ⁿ a; a¹  a ;

a ⁿ  ⁿ a^m (a  0, mZ, nN) ; (1.9) a⁰ 1 (a  0); a^p  ¹_p ( pR) ; (1.10) _a

(ab) ^p  a^pb^p ( p R) ; (1.11)

 a p ap

 b   p ( pR, b  0) ; (1.12)

_{ } _b

a^pa^q a^p^q ( p, qR) ; (1.13) ^aq^p  ^p^q ( p,qR) ; (1.14) a

(a ^p)^q  a ^pq ( p,qR) . (1.15)

Корені та їхні властивості

ⁿ ab_ ⁿ aⁿ b; n b^a _ ⁿ_n _b^a (b  0) ; (1.16)

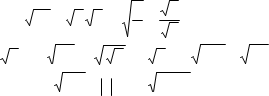n am  n am ; n m a  nma; nk amk  n am ; (1.17) ²ⁿ a²ⁿ  a ; ²ⁿ^1 a²ⁿ^1 _ a . (1.18)

§ 2. Перетворення логарифмічно-показникових виразів

Логарифмом числа b за основою a (a  0, a 1) називається показник степеня c , до якого треба піднести a , щоб отримати число b :

log_a b  c  a^c b (a  0, a 1).

Логарифмічна рівність ^log_a b  c і показникова рівність a^c b виражають одне й те саме співвідношення між числами a, b, c . За цими рівностями можна знайти одне з трьох чисел, що входять до них, якщо задано два інших. Відповідно до цього можна розв’язати три задачі на логарифми:

1) знайти число b за його логарифмом c і за основою a ; 2) знайти основу a за числом b і його логарифмом c ;

3) знайти логарифм c заданого числа b за даною основою a . Основні властивості логарифмів. Для будь-якого a  0, a 1справджуються рівності:

log _a1 0 ; (2.1) log _a a 1; (2.2)

a^log^{a x} x , якщо x  0 (2.3)

(співвідношення (2.3) – основна логарифмічна тотожність); log _a(xy)  log _a x  log _a y, якщо x  0, y  0 ; (2.4) x

log _a  log _a x  log _a y, якщо x  0, y  0 ; (2.5) y log _a x ^p  plog _a x , якщо x  0, pR; (2.6) log_a x _ log^b ^x , якщо x  0, b  0, b 1. (2.7) log_b a

Зокрема, log_ab  або log _a blog _b a 1; (2.8) log_b a

log _a b  log _ap b^p  plog _ap b _ ¹_p log_a b^p ( pR, p  0) . (2.9)

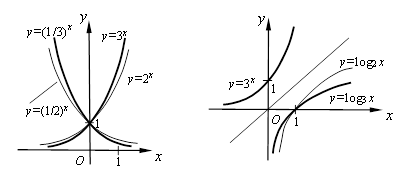
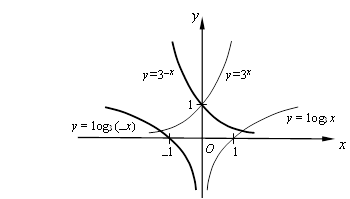
Графіки показникової та логарифмічної функцій

§ 3. Перетворення тригонометричних виразів

Співвідношення між тригонометричними функціями того самого аргументу

sin² xcos² x1; (3.1) sin x ^

tg x  , x  (2n1) , nZ ; (3.2) cos x 2 cos x

ctg x , x n, nZ ; (3.3) sin x

tg xctg x 1, x _^ⁿ , nZ ; (3.4)

1 tg² x  ¹₂ _x , x ^₂ (2n1) , nZ ; (3.5) _cos

1 ctg² x _ sin¹₂ _x , x n, nZ . (3.6)

Формули додавання sin( x y)  sin xcos y  cos xsin y ; (3.7) sin( x y)  sin xcos y  cos xsin y ; (3.8) cos(x y)  cos xcos y sin xsin y ; (3.9) cos(x y)  cos xcos y  sin xsin y ; (3.10)

tg(x y)  tg x^ ^{tg y} , x, y, x  y ^n, nZ ; (3.11)

1tg xtg y 2

tg(x y)  tg x^^{tg y} , x, y, x y ^n , nZ . (3.12)

1 tg xtg y 2

ctg(x  y)  ctg xctg y m1, ctg y  ctg x

x, y, x  y n, nZ. (3.12а)

Формули подвійного та потрійного аргументів

sin 2x  2sin xcosx ; (3.13)

cos2xcos²xsin²x2cos²x112sin²x ; (3.14)

2tg x ^{  }

tg2x  ₂ _x , x  ₄  ₂ k , k Z , x  ₂ n, nZ; (3.15)

₁__tg

ctg² x 1 

ctg2x  , x  n, nZ. (3.15а)

2ctg x 2

sin 3 3sin 4sin³; (3.16)

cos3 4cos³ 3cos; (3.17)

tg 3_ 31tg^3^tg^tg₂³^, _^₆ _^₃ k , _^₂ n, k,nZ. (3.17а)

Формули половинного аргументу

sin² ^x _ ¹^ ^{cos x} ; (3.18)

2 2

cos² ^x _ ¹^ ^{cos x} ; (3.19)

2 2

x sin x 1^ ^{cos x}

tg  _ , x  2n, nZ . (3.20)

2 1 cos x sin x

Формули перетворення суми на добуток

sin x sin y  2sin x^ ^y cos ^x^ ^y ; (3.21)

2 2

sin xsin y  2cos x^ ^y sin ^x^ ^y ; (3.22)

2 2

cos x cos y  2cos x^ ^y cos ^x^ ^y ; (3.23)

2 2

x y x y

cos x cos y  2sin sin ; (3.24)

2 2

sin( x

tg x  tg y _ ^ ^y⁾ , cos x cos y

sin( x

tg x  tg y _ ^ ^y⁾ ,

cos x cos y

x, y  ^ n , nZ ; (3.25) 2 x, y  ^ n, nZ . (3.26)

Формули перетворення добутку на суму

sin xsin y  (cos(x y)  cos(x y)) ; (3.27) cos xcos y  (cos(x y)  cos(x y)) ; (3.28) sin xcos y  (sin(x y)  sin( x y)) . (3.29)

Співвідношення між sinx, cosx , tgx та tg 2

x 2 tg sin x  ² , x  (2n 1), nZ ; (3.30)

1 tg2 x

1 tg² ^x cos x  ² , x  (2n 1), nZ ; (3.31)

1 tg² ^x

x 2 tg

tg x  2 , x   n, x  (2n 1), nZ . (3.32)

1 tg2 x 2

Формули зведення

Фун кція	Аргумент
		90_	90_	180	180_	270	270_	360
		 2	 2			3  2	3  2	2
sin x	sin	cos	cos	sin	sin	 cos	 cos	sin
cos x	cos	sin	sin	 cos	 cos	sin	sin	cos
tg x	tg	ctg	ctg	tg	tg	ctg	ctg	tg
ctgx	ctg	tg	tg	ctg	ctg	tg	tg	ctg

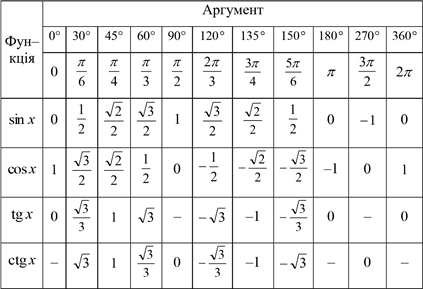
Значення тригонометричних функцій деяких кутів

Обернені тригонометричні функції

sin(arcsin x)  x, 1 x 1.	(3.33)
arcsin(sin x)  x, ^  x ^. 2 2	(3.34)
cos(arccosx)  x, 1 x 1.	(3.35)
arccos(cosx)  x, 0  x .	(3.36)
tg(arctgx)  x,   x  .	(3.37)
arctg(tgx)  x, ^  x ^. 2 2	(3.38)
ctg(arcctgx)  x,   x  .	(3.39)
arcctg(ctgx)  x, o  x .	(3.40)
arcsin x arccosx ^, 1 x 1.	(3.41)

   

     

arcsin(x)  arcsin x, 1 x 1.

(3.43)

arccos(x)  arccosx, 1 x 1.

(3.44)

arctgx arcctgx ^, x . ^(3.42)

arcsin x  arccos 1 x2  arctg x  arcctg 1 x2 ,

₁_ _x2 x (3.45)

0  x 1.

arccosx  arcsin 1 x2  arctg 1 x2  arcctg x ,

x ₁_ _x2 (3.46)

0  x 1. x 1 1

arctgx  arcsin  arccos  arcctg , 0  x  . (3.47)

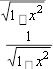
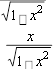arcctgx  arcsin  arccos  arctg , 0  x  . (3.48)

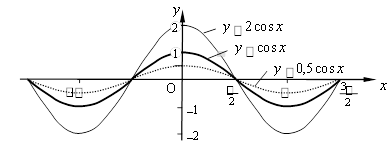
Графіки тригонометричних функцій

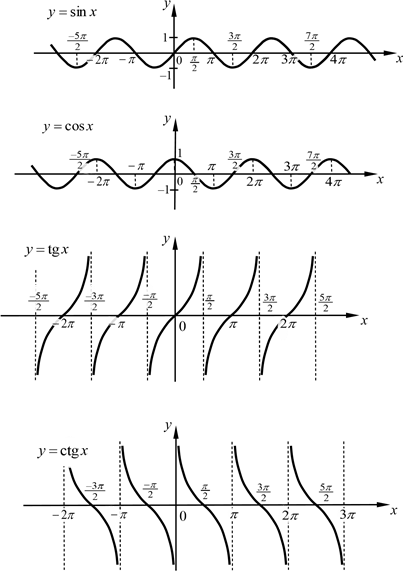
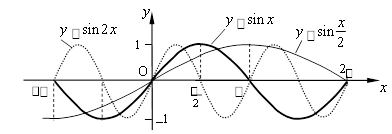
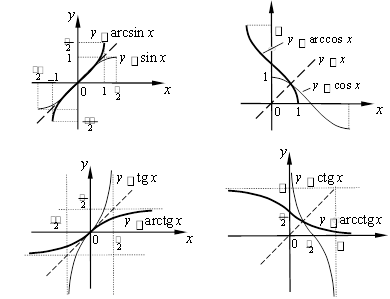
Графіки обернених тригонометричних функцій

§ 4. Алгебричні рівняння й нерівності

Якщо ліва і права частини рівняння є алгебричними виразами щодо невідомої (невідомих), то рівняння називають алгебричним. Якщо принаймні одна з частин рівняння містить невідому в аргументі трансцендентної функції (наприклад, показникової, логарифмічної, тригонометричної), то рівняння називають трансцендентним (неалгебричним).

Цілим раціональним алгебричним рівнянням називають рівняння, обидві частини якого є цілими раціональними алгебричними виразами або многочленами щодо невідомих. Раціональне алгебричне рівняння, яке містить бодай один дробовий раціональний вираз щодо невідомих, називають дробовим раціональним алгебричним рівнянням.

Розв’язком рівняння називають упорядковану сукупність значень невідомих, за яких рівняння обертається на правильну числову рівність.

Розв’язком нерівності з однією змінною називають значення змінної, за якого нерівність обертається на правильну числову нерівність.

Розв’язати рівняння (нерівність) означає знайти всі його розв’язки або довести, що розв’язків немає.

Два рівняння (нерівності) називають рівносильними, якщо вони мають ті самі розв’язки.

Рівняння (нерівності), які не мають розв’язків, також уважають рівносильними.

Основні властивості рівнянь

1. Якщо до обох частин рівняння додати одне й те саме число або вираз зі змінною, який не втрачає сенс в області визначення рівняння, то дістанемо рівняння рівносильне заданому.

2. Якщо обидві частини рівняння помножити або поділити на те саме число, що не дорівнює нулю, чи на вираз зі змінною, який не обертається на нуль за жодних значень змінної і не втрачає сенс на множині допустимих значень змінної для заданого рівняння, то дістанемо рівняння, рівносильне заданому.

3. На множині дійсних чисел рівняння f (x)  g(x) і f ²ⁿ^1(x)  g²ⁿ^1(x) , де n N , є рівносильними.

4. Якщо f (x)  0 і g(x)  0 , то на множині дійсних чисел рівносильними є рівняння f (x)  g(x) і f ²ⁿ(x)  g²ⁿ(x) , n N .

Властивості нерівностей з однією змінною

1. Якщо до обох частин нерівності додати одне й те саме число або вираз зі змінною, який не втрачає змісту в області визначення нерівності, то дістанемо нерівність рівносильну заданій. 2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число або вираз зі змінною, який набуває додатних значень за всіх значень змінної з області визначення нерівності, то дістанемо нерівність, рівносильну заданій.

3. Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число або на вираз зі змінною, який набуває від’ємних значень за всіх значень змінної з області визначення нерівності, і змінити при цьому знак нерівності на протилежний, то дістанемо нерівність, рівносильну заданій. f (x)

4. Якщо g(x)  0 , то нерівність  0 рівносильна нерівg(x) f (x)

ності f (x)g(x)  0 , а нерівність  0 рівносильна нерівності g(x)

f (x)g(x)  0 .

5. Якщо одна нерівність рівносильна другій, а друга рівносильна третій, то перша нерівність рівносильна третій.

§ 5. Ірраціональні рівняння та нерівності

Ірраціональним називається рівняння, в якому невідома змінна міститься під знаком кореня або під знаком піднесення до дробового степеня.

В елементарній математиці ірраціональні рівняння розглядаються на множині дійсних чисел, причому корені парного степеня вважаються арифметичними, а непарного – алгебричними.

Для розв’язування ірраціональних рівнянь використовують два методи: 1) метод піднесення обох частин рівняння до одного й того самого степеня і 2) метод введення нових змінних. Загальний метод розв’язування ірраціональних рівнянь полягає у тому, що спочатку ізолюють один радикал і обидві частини рівняння підносять до степеня, потім знову ізолюють радикал і обидві частини рівняння підносять до степеня і т.д.

На множині дійсних чисел піднесення обох частин рівняння до непарнного степеня приводить до рівносильного рівняння, а піднесення до парного степеня в загальному випадку порушує рівносильність рівнянь. Тому в разі піднесення до парного степеня перевірка знайдених значень невідомої змінної є обов’язковою, тобто є складовою частиною розв’язування рівняння.

Перед розв’язуванням ірраціонального рівняння доцільно знайти його область визначення, оскільки може виявитися, що це рівняння невизначене в області дійсних чисел. Розв’язуючи ірраціональні рівняння, слід мати на увазі, що ті значення невідомої змінної, які не належать області визначення рівняння, завжди є сторонніми коренями, а знайдені значення невідомого з області визначення обов’язково потрібно перевірити за умовою рівняння, оскільки вони також можуть виявитися сторонніми.

Ірраціональною нерівністю з однією невідомою називається нерівність, що містить невідому під знаком радикала. При розв’язуванні ірраціональних нерівностей, як і ірраціональних рівнянь, корені парного степеня розглядаються тільки арифметичні, а непарного степеня – на всій числовій прямій.

Для розв’язування ірраціональних нерівностей використовуються такі твердження:

1. Якщо нерівність, обидві частини якої невід’ємні за всіх значень невідомої з області допустимих значень, піднести до довільного натурального степеня, то отримана нерівність того самого знаку буде рівносильна заданій.

2. Якщо обидві частини нерівності піднести до непарного натурального степеня, то отримана нерівність того самого знаку буде рівносильна заданій.

3. Нерівність f (x)  g(x) (5.1)

рівносильна системі нерівностей:

 f (x)  0, 

g(x)  0,

_ f (x)  g(x)₂.

4. Нерівність

f (x)  g(x) (5.2)

рівносильна сукупності двох систем нерівностей:

 f (x)  0,

 f (x)  0, 

 g(x)  0,

g(x)  0;  2.

f (x)  g(x)

§ 6. Показникові рівняння та нерівності

Показниковим рівнянням називається рівняння, яке містить невідоме тільки в показниках степенів.

Загального методу розв’язування показникових рівнянь немає. Основні методи: 1) зведення обох частин показникового рівняння до спільної основи; 2) введення нової змінної.

Показниково-степеневе рівняння вигляду

g(x)^f^1(x)  g(x)^f^2(x) (6.1)

зводиться до розв’язування таких чотирьох рівнянь:

1) g(x) 1. Корені цього рівняння будуть коренями заданого рівняння, якщо існують функції ^f₁(x) і ^f₂(x) від цих коренів. 2) g(x)  1 . Корені цього рівняння будуть коренями заданого рівняння, якщо значення функцій ^f₁(x) та ^f₂(x) від цих коренів

– цілі числа однакової парності або нескоротні дроби з непарними знаменниками і чисельниками однакової парності. 3) g(x)  0 . Корені цього рівняння будуть коренями заданого, якщо значення функцій ^f₁(x) і ^f₂(x) від цих коренів додатні. 4) ^f₁(x)  ^f₂(x) . Корені цього рівняння будуть коренями заданого, якщо при значеннях x , які дорівнюють цим кореням, задане рівняння має зміст.

Для розв’язування показникових нерівностей використовують властивість монотонності показникової функції:

а) якщо a 1, то від нерівності a ^f ^(x) a^g^(x) переходять до нерівності f (x)  g(x) ;

б) якщо 0  a 1, то від нерівності a ^f ^(x) a^g^(x) переходять до нерівності f (x)  g(x) .

§ 7. Логарифмічні рівняння та нерівності

Логарифмічними рівняннями називають рівняння, які містять змінну під знаком логарифма.

Найпростіше логарифмічне рівняння має вигляд: log _a x  b , де a  0, a 1, bR .

Воно має єдиний розв’язок xa^b, який можна дістати за допомогою потенціювання.

Логарифмічне рівняння виду log _a f (x)  log _a g(x), де a  0 , a 1, (7.1)

рівносильне такій системі:

 f (x)  0, 

g(x)  0,

^ f (x)  g(x).

Інакше кажучи, аби розв’язати рівняння (7.1), досить розв’язати рівняння f (x)  g(x) і зі знайдених коренів вибрати ті, які задовольняють область визначення цього рівняння.

Для розв’язування логарифмічних рівнянь здебільшого використовують два методи:

1) метод, який полягає у перетворенні рівняння до вигляду log _a f (x)  log _a g(x);

2) метод введення нової змінної.

Показниково-логарифмічним рівнянням називається рівняння, яке містить змінну в показнику степеня під знаком логарифма. Такі рівняння за допомогою операції логарифмування зводяться до логарифмічних рівнянь.

Розв’язуючи нерівності виду log _a f (x)  log _a g(x) (7.2)

чи

log _a f (x)  log _a g(x), (7.3)

слід пам’ятати, що логарифмічна функція y  log _a x

зростає, якщо a 1, і спадає, якщо 0  a 1.

1. Якщо a 1, то нерівність (7.2) рівносильна системі нерівностей

 f (x)  0,

 g(x)  0,

_g(x)  0, звідки _  f (x)  g(x),  f (x)  g(x).



2. Якщо a 1, то нерівність (7.3) рівносильна системі нерівностей

 f (x)  0,

  f (x)  0,

_g(x)  0, звідки _  f (x)  g(x),  f (x)  g(x).



3. Якщо 0  a 1, то нерівності (7.2) і (7.3) рівносильні відповідно системам

 f (x)  0, g(x)  0,

 

_ f (x)  g(x); _ f (x)  g(x).

4. Розв’язування нерівностей виду ^log_(x) f (x)  k зводиться до розв’язування сукупності систем

_(x) 1, _0 (x) 1,

а) _ f (x) k (x); б) 0  f (x) k (x).

5. Нерівність виду ^log_(x) f (x)  k рівносильна сукупності систем

_(x) 1, _0 (x) 1,

а)  k (x); б)  f (x) k (x).

0  f (x) 

6. Нерівність виду ^log_(x) f (x)  ^log_(x) g(x) рівносильна сукупності систем нерівностей

(x) 1, 0 (x) 1,

а)  б) 

_ f (x)  g(x)  0; _0  f (x)  g(x).

7. Розв’язування нерівностей виду ^log_(x) f (x)  ^log_(x) g(x)

зводиться до розв’язування сукупності систем нерівностей

0 (x) 1, (x) 1,

а)  б) 

_ f (x)  g(x)  0, _0  f (x)  g(x).

§ 8. Рівняння та нерівності з модулями

Модуль (абсолютна величина) дійсного числа визначається так:

 a, якщо а  0, a  

_a, якщо а  0.

Геометрично a означає віддаль на координатній прямій від точки a до початку відліку (точка O ).

Властивості модулів

1) a  0 ; 6) a₁ a₂ ...a_n  a₁  a₂ ... a_n ;

2) a  a ; 7) a b  a  b ;

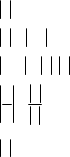
3) ab  a  b ; 8) якщо a  b , то b  a  b ; a a

4)  , b  0; 9) якщо a b, то або a  b , або a  b . b b

5) a²  a² .

Означення модуля використовується для розв’язування рівнянь і нерівностей з модулями.

1. f (x)  a. (8.1)

а) Якщо a  0 , то нерівність розв’язків не має;

б) якщо a  0 , то ця нерівність еквівалентна подвійній нерівності

a  f (x)  a .

2. f (x)  a. (8.2)

а) якщо a  0 , то розв’язком нерівності (8.2) буде область визначення функції f (x) ;

б) якщо a  0 , то нерівність (8.1) рівносильна сукупності нерівностей f (x)  a, f (x)  a.

§ 9. Тригонометричні рівняння та нерівності

Тригонометричним рівнянням називається рівняння, яке містить невідоме тільки в аргументі тригонометричної функції, причому над тригонометричними функціями виконуються тільки алгебричні дії.

Розв’язування тригонометричних рівнянь зводиться до розв’язування найпростіших тригонометричних рівнянь.

Найпростіші тригонометричні рівняння – це рівняння виду

1) sin x  a, де a 1; 2) cosxa, де a 1; 3) tgxa , де

a; 4) ctgx a, де a. Формули розв’язків цих рівнянь мають такий вигляд: sin x  a; x  (1)ⁿ arcsin a n, nZ ; (9.1) cos x  a; x  arccosa 2n , nZ ; (9.2) tgxa; xarctgan, nZ ; (9.3)

ctgxa; xarcctgan, nZ . (9.4)

В частинних випадках, коли a  0, a 1, a  1, формули роз-

в’язків набувають простішого вигляду, а саме:

sin x  0; x n, nZ ; sin x 1; x ^₂ 2n, nZ ; sin x 1; x ^₂ 2n, nZ ; cosx 0;x ^₂ n , nZ ; cos x 1; x  2n, nZ ; cos x  1; x  2n , nZ ; tg x  0; x n, nZ ; ctgx 0; x ^₂ n , nZ .

(9.5)

(9.6)

(9.7)

(9.8)

(9.9)

(9.10)

(9.11)

(9.12)

Розв’язування довільного тригонометричного рівняння за допомогою теорем рівносильності і тотожних перетворень завжди можна звести до розв’язування одного або кількох найпростіших тригонометричних рівнянь. Основні методи розв’язування тригонометричних рівнянь:

1) метод розкладення на множники;

2) метод уведення нової змінної;

3) метод уведення допоміжного аргументу;

4) універсальне тригонометричне підставлення (формули

(3.30) – (3.32)).

§ 10. Системи рівнянь та нерівностей

Нехай задано кілька рівнянь (або нерівностей, або рівнянь і нерівностей) з одними й тими ж змінними і нехай при цьому треба знайти розв’язки, спільні для всіх рівнянь (або нерівностей, або рівнянь і нерівностей). Тоді кажуть, що задано систему рівнянь (або нерівностей, або рівнянь і нерівностей).

Розв’язати систему означає знайти всі її розв’язки або довести, що система розв’язків немає.

Дві системи рівнянь (нерівностей) називаються рівносильними, якщо розв’язки першої системи є розв’язками другої і навпаки, розв’язки другої системи є розв’язками першої. Системи, які не мають розв’язків, також називаються рівносильними.

Розв’язуючи системи рівнянь, користуються такими правилами перетворення систем на рівносильні:

1) Правило підставлення. Якщо одну зі змінних системи з якого-небудь рівняння виразити через решту змінних і підставити отриманий вираз замість цієї змінної в інші рівняння, то дістанемо систему, рівносильну заданій.

2) Правило додавання. Якщо до одного з рівнянь системи додати почленно інше рівняння, помножене на деяке відмінне од нуля число, то дістанемо систему, рівносильну заданій.

3) Правило заміни. Якщо одне з рівнянь системи замінити на рівносильне, то дістанемо систему, рівносильну заданій. Щоби розв’язати систему нерівностей з однією змінною, потрібно розв’язати кожну нерівність системи окремо, а потім знайти їх спільні розв’язки.

§ 11. Похідна функції та її застосування

Похідна функції y  f (x) у точці ^x₀ – це границя відношення приросту y функції до приросту x аргументу за умови, що x  0, а границя існує:

f (x0)  lim y  lim f (x0 x)  f (x0) .

x0 x x0 x

Геометричний зміст похідної: похідна f (^x₀) дорівнює кутовому коефіцієнтові дотичної до кривої y  f (x) , проведеної у точці (x₀, y₀) .

Основні правила диференціювання

( f  g)  f  g;

( f  g)' f 'g  f  g';

(cg)' cg', (c const) ;



 f  f g  f g  _g _  _g2 , g  0 .

_

Рівняння дотичної до графіка функції y  f(x) у точці (x₀, y₀): y  f (x₀)  f (x₀)(x  x₀).

Схема дослідження функції 1. Знайти область визначення.

2. З’ясувати, чи є функція:

а) парною або непарною;

б) періодичною.

3. Обчислити координати точок перетину графіка функції з вісями координат.

4. Знайти проміжки знакосталості функції.

5. Знайти проміжки зростання та спадання.

6. Знайти точки екстремуму функції і обчислити її значення в цих точках.

7. Дослідити функцію, коли x  .

8. Побудувати графік функції.

Таблиця похідних

1. (x^) x^1, (R) (u^)'u^1u'

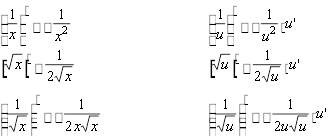
1.1.

1.2.

1.3.

2. (a^x)' a^x ln a, (a  0, a 1) (a^u )' a^u  ln au

3. (e^x )  e^x (e^u )' e^u u'

1 1

4. (log_a x)' , (a  0, a 1) (log_au)' u xln a uln a

1 1

5. (ln x)' (ln u)' u x u

6. (sin x)' cos x (sin u)' cosuu'

7. (cosx)' sin x (cosu)' sin uu'

1 1

8. (tg x)' 2 x (tgu)' cos₂u u'

cos

1 1

9. (ctg x)'  (ctgu)'  u'

10. 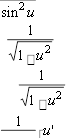(arcsin x)'(arcsinu)' u'

11. (arccosx)'  (arccosu)'  u'

12. (arctgx)' 1 x₂ (arctgu)' 1u₂

1 1

13. (arcctgx)'  2 (arcctgu)' 1_u2 u'

1_ x

§ 12. Первісна та інтеграл

Функція F називається первісною для функції f на заданому проміжку I , якщо для всіх x із цього проміжку F'(x)  f (x). Основна властивість первісних. Загальний вигляд первісних для функції f (x) на проміжку I є

F(x) C ,

де C – довільна стала, а F(x) – одна з первісних для функції f (x) на проміжку I .

Три правила відшукання первісних

1. Якщо F – первісна для f , а G – первісна для g , то F  G – первісна для f  g .

2. Якщо F – первісна для f , а k – стала, то kF – первісна для kf .

3. Якщо F(x) – первісна для функції f (x) , а k і b – сталі,

причому k  0, то  F(kxb) – первісна для функції f (kxb) . k

Сукупність усіх первісних функції f (x) називаєься невизначеним інтегралом від цієї функції і позначається символом  f (x)dx . Згідно з означенням  f (x)dx F(x)C .

Властивості невизначеного інтеграла 1. (f  g)dx  fdx gdx.

2. afdx a fdx, де aconst .

3. Якщо

 f (x)dx F(x)C ,

то

 f (kxb)dx  k F(kxb) С ,

де k, bconst , С – довільна стала.

Формула Ньютона-Ляйбніца  f (x)dx  F(b)  F(a) .

Таблиця невизначених інтегралів

^dx  x1 C , ( 1) .

1.  x __₁

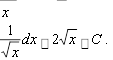1.1. dx 1dx x⁰ dx xC. 1.2. _ ¹₂ dx  _ ¹_x C .

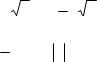1.3.  xdx  ₃ x x C . 1.4. 

2. ^ _x dx  ln x C .

3. sin xdx cosx C .

4. cosxdxsin xC .

5. ^ _{sin 2} _x dx  ctg x C , (x  k, kZ) .

1 ^

6. ^ _cos2 _x dx  tg x C , (x ^ ₂  k, kZ).

7. tgxdx ln cosx C , (x ^₂  k, kZ).

8. ctgxdx lnsin x C , (x  k, kZ) .

9. e^xdxe^x C .

^xdx  ax C , (a  0, a 1) .

10. a _{ln a}

dx x x

11. ^ _a₂ _ _x₂  arcsin _a  C  arccos_a  C , (a  0, x  a) .

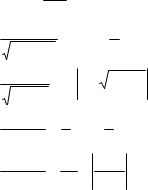dx ² a C , (a  0, x²  a  0) . 12. ^ _x₂ _ _a  ln x  x 

dx 1 x

13. ^ _x2 _ _a2  _a arctg _a C , (a  0) .

14.  x2dxa2  21a ln xxaa C , (a  0) .

§ 13. Прогресії

Арифметична прогресія (^a₁ – перший член; d – різниця; n – кількість членів; ^a_n – n -й член; ^S_n – сума n перших членів):

a_n  a₁  d(n 1) ; (13.1)

S_n  a¹ ^^an n _ ^2a1 ^^d⁽ⁿ^¹⁾ _n; (13.2)

2 2

a^k^1 ^ ^ak^1 , k  2, 3, ..., n1; (13.3) a_k 

2 a_k  a_m  a_p  a_q, де k  m  p  q. (13.4)

Геометрична прогресія (^b₁ – перший член; q – знаменник

( q  0); n – кількість членів; b_n – n -й член (b_n  0) ; S_n – сума n перших членів):

b_n  b₁qⁿ^1 ; (13.5) b¹(¹qⁿ⁾ (q 1) ; (13.6)

S_n 

1q

b_k²  b_k_1b_k_1, k  2; 3; ...; n 1; (13.7) b_kb_m  b_pb_q, де k  m  p  q. (13.8) Якщо q 1, то за необмеженого збільшення n (n ) сума

b¹ , яке називають сумою нескінченної

^S_n прямує до числа

1 q

геометричної прогресії і позначають літерою S :

b¹ . (13.9)

S 

1 q

§ 14. Відсотки

Відсотком (процентом) називається одна сота частина числа (або величини).

Виходячи з означення, маємо:

1%   0.01 ; 3%   0.03 ;

65.5%  0.655 ; 125% 1.25 ; 401%  4.01. Три основні типи задач на відсотки

1. Знаходження відсотка від даного числа. Щоби знайти k відсотків від даного числа A , треба число A поділити на 100%

і помножити на k% : k% . 100%

Приклад 1. У банк поклали 3000 грн. під 8% річних. На скільки гривень зросте величина вкладу через рік? Розв’язання. Потрібно знайти 8% від 3000 грн.:

3000

8%  3000  0.08  240 (грн.).

100%

Відповідь. 240 грн.

2. Знаходження числа за його відсотком. Щоби знайти невідоме число X , k% якого становить B , треба B поділити на

k% і помножити на 100% : X _ ^B^^100% . k%

Приклад 2. У банк поклали певну суму під 8% річних. Якою була величина початкового вкладу, якщо через рік вклад зріс на 240 грн.?

Розв’язання. Потрібно знайти величину вкладу, якщо 8% від нього становить 240 грн.:

240 100%  3000 (грн.).

Відповідь. 3000 грн.

3. Знаходження відсоткового відношення двох чисел (вираження одного числа у відсотках другого). Щоби знайти відсоткове відношення двох чисел, потрібно відношення цих чисел помножити на 100% .

Приклад 3. У банк поклали 3000 грн. Через рік сума вкладу збільшилася на 240 грн. Під який відсоток поклали вклад? Розв’язання.

100%  8% .

Відповідь. 8% .

Щоби знайти на скільки відсотків збільшилась або зменшилася певна величина, треба знайти:

1) на скільки одиниць збільшилась або зменшилася ця величина;

2) скільки відсотків становить знайдена різниця від початкового значення величини.

Збільшенню у 2 рази відповідає збільшення на 100% , а зменшенню у 2 рази – зменшення на 50% .

Вкладений у банк початковий капітал ^K₀ під p% річних через n років перетвориться в нарощений капітал ^K_n , який обчислюється за формулою складних відсотків:

K_n  K₀ 1 p n,

 100 

p де r 1 – коефіцієнт складного відсотка. 100

Приклад 4. До банку зроблено внесок $100000 під 3% річних. Яку суму виплатить банк через 10 років?

Розв’язання. K₁₀ 100000 (10.03)¹⁰ 134392($) . Відповідь. $134392 .

Заувага. Якщо немає таблиць коефіцієнтів складних відсотків, можна скористатись таблицями десяткових логарифмів. Тоді

lg K₁₀  lg100000 10lg1.03  510lg1.03, звідки K₁₀ 134392 .

§ 15. Планіметрія

Основні теореми

Трикутник

Теорема 15.1 (перша ознака рівності трикутників). Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.

Теорема 15.2 (друга ознака рівності трикутників). Якщо сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні.

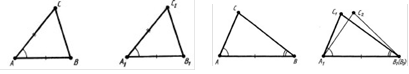
До теореми 15.1 До теореми 15.2

Теорема 15.3 (третя ознака рівності трикутників). Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні. Теорема 15.4 (теорема Піфагора). У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

Теорема 15.5 (теорема косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними. Теорема 15.6 (теорема синусів). Сторони трикутника пропорційні до синусів протилежних кутів.

Теорема 15.7 (про зовнішній кут трикутника). Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних із ним.

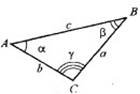
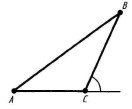
До теореми 15.5 До теореми 15.7

Теорема 15.8 (про середню лінію трикутника). Середня лінія трикутника, яка сполучає середини двох даних сторін, паралельна третій стороні і дорівнює її половині.

Теорема 15.9 (перша ознака подібності трикутників). Якщо два кути одного трикутника відповідно дорівнюють двом кутам другого трикутника, то такі трикутники подібні.

Теорема 15.10 (друга ознака подібності трикутників). Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то трикутники подібні. Теорема 15.11 (третя ознака подібності трикутників). Якщо сторони одного трикутника пропорційні сторонам другого трикутника, то такі трикутники подібні.

Для подібності двох прямокутних трикутників досить, щоб у них було по рівному гострому куту.

Теорема 15.12. Катет прямокутного трикутника є середнім пропорційним між гіпотенузою і проекцією цього катета на гіпотенузу.

AB BC

 або BC  ABBD .

BC BD

Теорема 15.13. Висота прямокутного трикутника, проведена з вершини прямого кута, є середнім пропорційним між проекціями катетів на гіпотенузу.

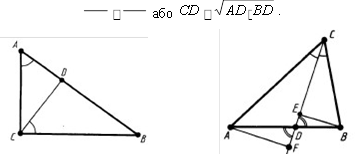AD CD

CD BD

До теорем 15.12, 15.13 До теореми 15.14

Теорема 15.14. Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам.

AC AD



BC BD

Теорема 15.15 (нерівність трикутника). Які б не були три точки, віддаль між будь-якими двома з цих точок не більша від суми віддалей від них до третьої точки.

У будь-якому трикутнику кожна сторона менша за суму двох інших сторін.

Теорема 15.16. Медіани трикутника перетинаються в одній точці, яка ділить кожну медіану у відношенні 2 :1, починаючи від вершини трикутника.

Чотирикутники

Паралелограм – це чотирикутник, протилежні сторони якого попарно паралельні.

Теорема 15.17. Якщо діагоналі чотирикутника перетинаються і в точці перетину діляться навпіл, то цей чотирикутник – паралелограм.

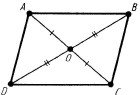
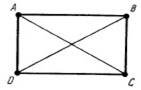
До теореми 15.17 До теореми 15.21

Теорема 15.18 (обернена до теореми 15.17). Діагоналі паралелограма перетинаються і в точці перетину діляться навпіл. Теорема 15.19. У паралелограма протилежні сторони рівні, протилежні кути рівні.

Теорема 15.20. Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.

Прямокутник – це паралелограм, в якого всі кути прямі.

Теорема 15.21. Діагоналі прямокутника рівні.

Ромб – це паралелограм, в якого всі сторони рівні.

Теорема 15.22. Діагоналі ромба перетинаються під прямим кутом. Діагоналі ромба є бісектрисами його кутів.

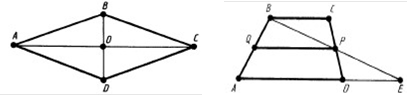
До теореми 15.22 До теореми 15.23 Квадрат – це прямокутник, в якого всі сторони рівні. Оскільки сторони квадрата рівні, то він є ромбом. Тому квадрат має властивості прямокутника і ромба.

Трапеція – це чотирикутник, у якого тільки дві протилежні сторони паралельні.

Теорема 15.23. Середня лінія трапеції паралельна основам і дорівнює їх півсумі.

Коло

Теорема 15.24. Центр кола, описаного навколо трикутника, є точкою перетину перпендикулярів до сторін трикутника, проведених через середини цих сторін.

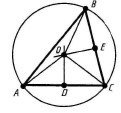
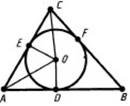
До теореми 15.24 До теореми 15.25

Теорема 15.25. Центр кола, вписаного в трикутник, є точкою перетину його бісектрис.

Кут, вершина якого лежить на колі, а сторони перетинають це коло, називається вписаним у коло.

Теорема 15.26. Кут, вписаний у коло, дорівнює половині відповідного центрального кута.

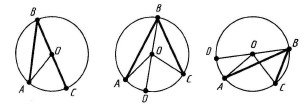
До теореми 15.26

Вписані кути, сторони яких проходять через точки A і B кола, а вершини лежать з одного боку від прямої AB, рівні.

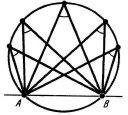
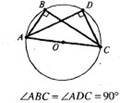
Вписані кути, які спираються на діаметр, прямі.

Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи.

Теорема 15.27. Якщо хорди AB і CD кола перетинаються в точці S , то AS BS  CS DS .

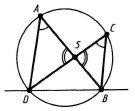
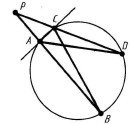
До теореми 15.27 До теореми 15.28

Теорема 15.28. Якщо з точки P до кола проведено дві січні, які перетинають коло відповідно в точках A, B і C, D , то APBP  CP DP .

Теорема 15.29. Кут із вершиною поза колом вимірюється піврізницею дуг, які знаходяться між сторонами кута.

Теорема 15.30. Кут, утворений дотичною і хордою, дорівнює половині дуги, яка знаходиться між його сторонами.

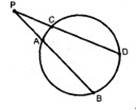
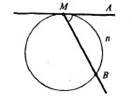
BPD  BDAC AMB  ^MnB

До теореми 15.29 До теореми 15.30

Якщо у чотирикутнику суми протилежних кутів дорівнюють 180^o , то навколо нього можна описати коло.

Якщо в опуклому чотирикутнику суми протилежних сторін рівні, то в нього можна вписати коло.

Теорема 15.31 (теорема Фалеса). Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні.

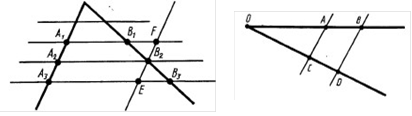
До теореми 15.31 До теореми 15.32

Теорема 15.32 (про пропорційні відрізки). Паралельні прямі, які перетинають сторони кута, відтинають від сторін кута пропорційні відрізки.

Теорема 15.33. Площі подібних фігур відносяться як квадрати їхніх відповідних лінійних розмірів.

Основні формули

Співвідношення в довільному трикутнику (a, b, c – сторони;

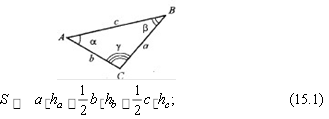
, ,  – протилежні їм кути; p – півпериметр; R – радіус описаного кола; r – радіус уписаного кола; S – площа; ^h_a – висота, проведена до сторони a ):

S  bcsin acsin  absin; (15.2)

S  p(p  a)(p b)(p  c) (формула Герона); (15.3) abc

S  pr ; (15.4) S  ; (15.5)

a² b²c²2bccos (теорема косинусів); (15.6) a b c

   2R (теорема синусів та її наслідок). (15.7)

sin sin sin

Співвідношення у прямокутному трикутнику (a, b – катети; c – гіпотенуза; ^h_c – висота, проведена з вершини прямого кута; a_c, ^b_c – проекції катетів на гіпотенузу):

a² b² c² (теорема Піфагора); (15.8) S  ab ; (15.9) S  ch_c; (15.10) r _ a ^ ^b ^ ^c ; (15.11) R _ ^c ; (15.12) 2 2

a  csin ccosbtgbctg; (15.13)

ac  hc ; (15.14) ac  a ; (15.15) bc  b . (15.16) h_c b_c a c b c

Співвідношення в рівносторонньому трикутнику зі стороною a:

a² 3 a 3 a 3

S ; (15.17) r ; (15.18) R . (15.19)

4 6 3

Співвідношення в паралелограмі (a і b – суміжні сторони;

 – кут між ними; ^h_a – висота, проведена до сторони a ; ^d₁, ^d₂ – діагоналі;  – кут між діагоналями; S – площа):

S  ah_a ; (15.20) S  a bsin; (15.21)

1 ² d₂²  2(a² b²). (15.23)

S  d₁d₂ sin; (15.22) d₁  2

Трапеція (a, b – основи; h – висота; l – середня лінія): l _ a ^ ^b ; (15.24) S _ ^a ^^b _h  l h. (15.25)

2 2

Правильний многокутник (^a_n – сторона правильного n кутника; R – радіус описаного кола; r – радіус уписаного кола):

a⁴ ; (15.28) r _ ^a⁴ ; (15.29) R  a₆ ; (15.30)

R _

2 2

a⁶ ^ ³ ; (15.31) S _ ⁿ^^an ^^r . (15.32)

r _

2 2

Якщо діагоналі чотирикутника перетинаються, то площа чотирикутника дорівнює половині добутку його діагоналей на синус кута між ними.

Якщо в опуклому чотирикутнику діагоналі перпендикулярні, то його площа дорівнює половині добутку діагоналей.

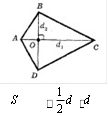
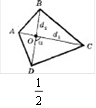SABCD  d1d2 sin ABCD 1 2

Коло, круг ( R – радіус; C – довжина кола; S – площа круга):

C  2R ; (15.33) SR² ; (15.34)

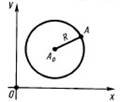
(x  a)²  (y b)²  R² (15.35)

(рівняння кола з центром у точці ^A₀(a; b)).

Круговим сектором називається частина круга, яка лежить усередині відповідного центрального кута.

Сектор (l – довжина дуги кола, яка відповідає центральному кутові n^o ;  – радіанна міра центрального кута; S – площа сектора):

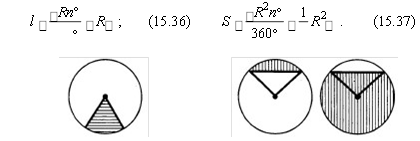180 2

Круговий сектор Круговий сегмент

Круговим сегментом називається спільна частина круга і півплощини.

Площа сегмента, що не дорівнює півкругу, обчислюється за

формулою S  R2 no  S, 3600

де n^o – градусна міра центрального кута, який містить дугу кругового сегмента, а ^S_ – площа трикутника з вершинами в центрі круга і на кінцях радіусів, які обмежують даний сектор.

Знак «+» треба брати, коли n^o 180^o , а знак «–» – тоді, коли n^o 180^o

§ 16. Стереометрія

Аксіоми та теореми Аксіоми стереометрії та їх наслідки.

Аксіома 1. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй.

Аксіома 2. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку. Аксіома 3. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.

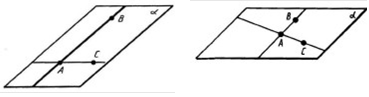
До теореми 16.1 До теореми 16.3

Теорема 16.1. Через пряму і точку, яка не лежить на ній, можна провести площину, і до того ж тільки одну.

Теорема 16.2. Якщо дві точки прямої належать пощині, то вся пряма належить цій площині.

Теорема 16.3. Через три точки, які не лежать на одній прямій, можна провести площину, і до того ж тільки одну.

Паралельність прямих та площин.

Дві прямі називаються паралельними, якщо вони лежать в одній площині і не перетинаються.

Пряма і площина або дві площини називаються паралельними, якщо вони не мають спільних точок.

Теорема 16.4. Через точку, яка не лежить на заданій прямій, можна провести пряму, паралельну цій прямій, і до того ж тільки одну.

Теорема 16.5 (ознака паралельності прямих). Дві прямі, паралельні до третьої прямої, паралельні між собою. Теорема 16.6 (ознака паралельності прямої та площини). Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині.

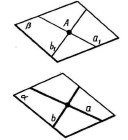
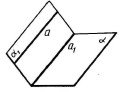
До теореми 16.6 До теореми 16.7

Теорема 16.7 (ознака паралельності площин). Якщо дві прямі, які перетинаються, однієї площини відповідно паралельні двом прямим другої площини, то ці площини паралельні.

Теорема 16.8. Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну. Теорема 16.9. Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.

Теорема 16.10. Відрізки паралельних прямих, які містяться між двома паралельними площинами, рівні.

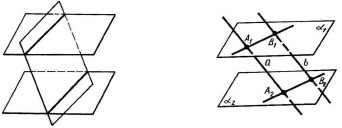
До теореми 16.9 До теореми 16.10

Перпендикулярність прямих і площин.

Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

Пряма, яка перетинає площину, називається перпендикулярною до цієї пощини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині і проходить через точку перетину. Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих площин, перетинає їх по перпендикулярних прямих.

Теорема 16.11 (ознака перпендикулярності прямих). Якщо дві прямі, які перетинаються, паралельні відповідно двом перпендикулярним прямим, то вони також перпендикулярні. Теорема 16.12 (ознака перпендикулярності прямої і площини). Якщо пряма перпендикулярна до двох прямих, які лежать у площині і перетинаються, то вона перпендикулярна до даної площини.

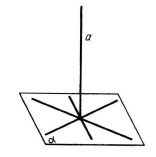
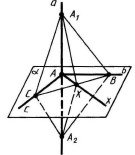
До означення a  До теореми 16.12

Теорема 16.13. Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.

Теорема 16.14. Дві прямі, перпендикулярні до однієї і тієї самої площини, паралельні.

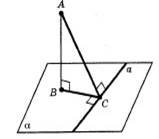
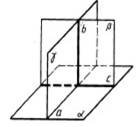
До теореми 16.15 До теореми 16.16

Теорема 16.15 (про три перпендикуляри). Якщо пряма, проведена на площині, перпендикулярна до проекції похилої на цю площину, то вона перпендикулярна і до самої похилої. І навпаки: якщо пряма на площині, перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої на цю площину.

Теорема 16.16 (ознака перпендикулярності двох площин). Якщо площина проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.

Теорема 16.17. Якщо деяка точка простору рівновіддалена від усіх вершин довільного плоского многокутника, то її ортогональна проекція на площину цього многокутника є центром описаного навколо нього кола.

Справедлива також обернена теорема.

Теорема 16.18. Якщо задана точка простору рівновіддалена від усіх сторін плоского многокутника, то ортогональна проекція цієї точки на площину многокутника є центром кола, вписаного в цей многокутник.

Справедлива також обернена теорема.

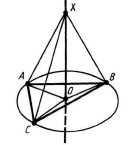
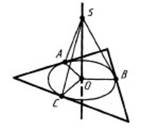
До теореми 16.17 До теореми 16.18

Теорема 16.19 (про площу ортогональної проекції многокутника). Площа ортогональної проекції многокутника на площину дорівнює добуткові його площі на косинус кута між площиною многокуника і площиною проекції.

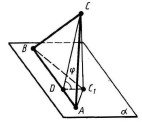
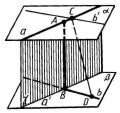
До теореми 16.19 Мимобіжні прямі Мимобіжні прямі.

Прямі, які не перетинаються і не лежать в одній площині, називаються мимобіжними.

Спільним перпендикуляром до двох мимобіжних прямих називається відрізок з кінцями на цих прямих, перпендикулярний до кожної з них.

Дві мимобіжні прямі завжди мають спільний перпендикуляр і до того ж тільки один.

Через дві мимобіжні прямі можна провести паралельні площини, і до того ж єдиним чином.

Віддалю між мимобіжними прямими називається довжина їхнього спільного перпендикуляра. Віддаль між мимобіжними прямими дорівнює віддалі між паралельними площинами, які проходять через ці прямі.

Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і паралельні заданим мимобіжним прямим.

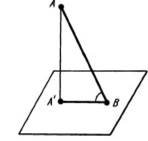
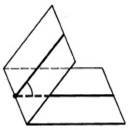
Кут між прямою і площиною Кут між площинами

Основні формули

Довільна призма (l – бічне ребро; P – периметр основи; S – площа основи; H – висота; ^P_п.n. – периметр перпендикулярного перерізу; ^S_п.n. – площа перпендикулярного перерізу; ^S_біч – площа бічної поверхні; V – об’єм):

S_біч  P_п_.n. l ; (16.1) V  SH ; (16.2) V  S_п_.n. l . (16.3) Пряма призма: S_біч  Pl . (16.4)

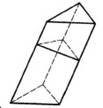
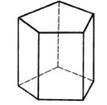
Прямокутний паралелепіпед (a, b, c – його виміри; d – діагональ):

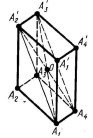
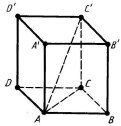
V  abc ; (16.5) d² a² b² c². (16.6)

Довільна піраміда (S – площа основи; H – висота; V – об’єм):

V SH . (16.7)

Правильна піраміда ( P – периметр основи; l – апофема; ^S_біч

– площа бічної поверхні):

S_біч _ ¹₂ Pl ; (16.8) V SH . (16.9)

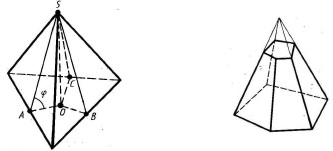
Довільна зрізана піраміда (^S₁ і ^S₂ – площі основ; h – висота; V – об’єм):

V  ¹₃ h(S₁ S₂  S₁S₂ ) . (16.10)

Тіла обертання:

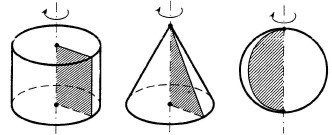
Циліндр ( R – радіус основи; H – висота; ^S_біч – площа бічної поверхні; V – об’єм):

S_біч  2RH ; (16.11) V R²H . (16.12)

Конус ( R – радіус основи; H – висота; l – твірна; ^S_біч – площа бічної поверхні; V – об’єм):

S_біч Rl ; (16.13) V _ ¹₃R²H . (16.14)

Бічна поверхня зрізаного конуса (^r₁ та ^r₂ – радіуси основ, l – твірна):

S_біч_. (r₁  r₂)l . (16.15)

Переріз кулі площиною:

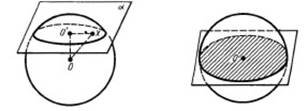
Куля, сфера ( R – радіус кулі; S – площа сферичної поверхні; V – об’єм):

S 4R² ; (16.16) V  ₃⁴R³ . (16.17)

Кульовий сегмент ( R – радіус кулі; h – висота сегмента; S – площа сферичної поверхні сегмента; V – об’єм):

S  2Rh ; (16.18) V h²R  h. (16.19)

Кульовий сектор ( R – радіус кулі; h – висота відповідного кульового сегмента; V – об’єм):

V  ₃²R²h . (16.20)

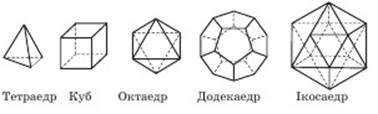
Опуклі многогранники, всі грані яких правильні многокутники, називаються правильними многогранниками

Вписана і описана призми:

Вписана і описана піраміди:

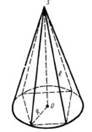
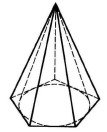
§ 17. Вектори

Вектором називається напрямлений відрізок. Координатами

вектора ^A₁^A₂ a з початком у точці ^A₁(^x₁; ^y₁; ^z₁) і кінцем у точці A2(x2; y2; z2) називаються числа a1  x2  x1 , a2  y2  y1,

a₃  ^z₂  ^z₁ . За допомогою координат вектор позначають так:

r r

a(a₁; a₂; a₃) або a  (a₁; a₂; a₃) .

Рівні вектори мають відповідно рівні координати, і навпаки,

вектори з відповідно рівними координатами рівні.

r r

Сумою векторів a(a₁; a₂; a₃) і b(b₁; b₂; b₃) називається

вектор c(a₁  b₁; a₂  b₂; a₃  b₃).

Для будь-яких точок A, A, C справджується векторна рівність:

AB  BC  AC .

Модулем (абсолютною величиною) вектора a(^a₁; ^a₂; ^a₃) називається довжина відрізка, що зображає вектор. Тому

r 2 a22  a32 . a  a1 

Добутком вектора a(^a₁; ^a₂; ^a₃) на число  називається

вектор a  (a₁; a₂; a₃) .

r r

Абсолютна величина вектора a дорівнює  a , а напрям

збігається з напрямом вектора a , якщо  0, і протилежний

напряму вектора a , якщо  0 .

Два ненульові вектори називаються колінеарними, якщо вони r

лежать на одній прямій або на паралельних прямих. Якщо a та r b – відмінні од нуля колінеарні вектори, то існує число  таке, що

r r

b a .

r r

Скалярним добутком векторів a(a₁; a₂; a₃) і b(b₁; b₂; b₃) називається число a1b1  a2b2  a3b3 .

r r r² і називають

Скалярний добуток aa позначають a

скалярним квадратом. Очевидно, ar²  ar ²; ar  ar² .

r r

Скалярний добуток векторів a та b дорівнює добуткові їхніх абсолютних величин на косинус кута  між ними:

r r r r ab  a  b cos.

Кут  між векторами a(a₁; a₂; a₃) та b(b₁; b₂; b₃) визначається за формулою cos ab  a1b1  a2b2  a3b3 .

a  b a₁2  a₂2  a₃2  b₁2 b₂2 b₃2

Якщо вектори перпендикулярні, то скалярний добуток цих векторів дорівнює нулеві. І навпаки, якщо скалярний добуток відмінних од нуля векторів дорівнює нулеві, то ці вектори перпендикулярні.

Вектор називається одиничним, якщо його модуль дорівнює

r r r

одиниці. Одиничні вектори e₁(1;0;0) , e₂(0;1;0) , e₃(0;0;1) , які мають напрями додатних координатних піввісей, називають

базовими векторами або ортами. r

Будь-який вектор a(^a₁;^a₂;^a₃) можна записати у вигляді

лінійної комбінації базових векторів:

r r r r

a  a₁e₁  a₂e₂  a₃e₃ ,

де числа ^a₁ , ^a₂ , ^a₃ – координати вектора.

§ 18. Елементи комбінаторики.

Початки теорії ймовірностей

Елементи комбінаторики

Комбінаторика – це розділ математики, що розв’язує задачі про вибір та розміщення елементів скінченої множини згідно з певними правилами.

Скінченна множина називається впорядкованою, якщо її елементи занумеровані натуральними числами, тобто кожен елемент має порядковий номер.

Є три види сполук: переставлення, розміщення, комбінації. Переставлення з n елементів – це будь-яка впорядкована множина з n елементів. Кількість переставлень з n елементів

P_n  n!,

де n!123Kn (n! читаємо „n -факторіал”). За означенням 1!1, 0!1.

Розміщення з n елементів по m – це будь-яка впорядкована підмножина M , яка складається з m елементів, даної множини N , яка складається з n елементів (m  n) .

Кількість розміщень з n елементів по m

A_nm  n^! .

nm! Комбінація з n елементів по m – це будь-яка підмножина M , яка складається з m елементів, даної множини N , яка складається з n елементів (m  n) .

Кількість комбінацій з n елементів по m

C_nm  n^! . m!nm!

Властивості комбінацій

1. C_n^m  C_nⁿ^m; 2. C_n^m^1 _ ⁿ^^m C_n^m;

m1

3. C_n^m C_n^m^1  C_n^m_^₁¹; 4. C_n⁰ C_n¹ C_n² ...C_nⁿ  2ⁿ .

5. C_nⁿ  C_n⁰  C₀⁰ 1

Трикутник Паскаля:

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 . . . . . . . . . . . . . . . . . . . . . . . . . .

Біном Ньютона дає розвинення (розгорнення) n -го степеня двочлена a b у вигляді многочлена за степенями a та b :

(a  b)n  Cn0an Cn1an1b Cn2an2b2 ...Cnmanmbm ...Cnnbn .

Коефіцієнти розвинення (a b)ⁿ (біномні коефіцієнти) збігаються з (n1)-м рядком трикутника Паскаля.

Властивості розвинення бінома Ньютона

1. Кількість членів розвинення бінома Ньютона на одиницю більша за показник степеня бінома.

2. Загальний член розвинення обчислюється за формулою T_k_1  C_nkankbk .

3. Коефіцієнти членів, рівновіддалених від початку і кінця розвинення, рівні між собою.

4. Сума біномних коефіцієнтів дорівнює 2ⁿ .

5. Сума біномних коефіцієнтів, які стоять на парних місцях, дорівнює сумі біномних коефіцієнтів, які стоять на непарних місцях.

Основні поняття теорії ймовірностей

Подія – це будь-який факт, який є результатом досліду (випробування). Під випробуванням розуміють здійснення певного комплексу умов.

Подія, яка може відбутися або не відбутися за даних умов, називається випадковою (можливою) подією. Події позначають великими літерами латинської абетки A, B , C тощо.

Хоча результат окремого випробування є випадковою подією, за багатократного повторення випробувань виявляються певні закономірності. Прояв тих закономірностей є наслідком певного, цілком визначеного зв’язку між комплексом умов та подією A.

Подія, яка неминуче відбудеться за даного випробування, називається вірогідною. Вірогідну подію позначають літерою U .

Подія, яка не може відбутися за умов даного випробування, називається неможливою. Неможливу подію позначають символом Ǿ.

Випадкові події A та B називаються несумісними в даному випробуванні, якщо вони не можуть відбутися водночас. Події A та B називаються сумісними, якщо в даному випробуванні вони можуть відбутися разом (тобто можливе суміщення подій A й B ).

Події ^A₁, ^A₂ , …, ^A_n називаються попарно несумісними в даному випробуванні, якщо жодні дві з них не можуть відбутися разом (водночас).

Множина подій у даному досліді утворює повну групу подій, якщо в результаті випробування обов’язково наступить принаймні одна з цих подій. Іншими словами, множина всіх можливих найпростіших результатів випробування утворює повну групу подій

Події ^A₁, ^A₂ , …, ^A_n вважаються рівноможливими, якщо немає підстав сподіватися, що якась із них появлятиметься частіше за іншу під час багаторазових випробувань, які провадяться за однакових умов.

Події, які 1) утворюють повну групу, 2) є несумісними і 3) рівноможливими називають елементарними подіями.

Ймовірністю PAвипадкової події A називають відношення кількості m елементарних подій, які сприяють цій події, до загальної кількості n всіх рівноможливих несумісних подій, які утворюють повну групу в даному випробуванні:

PA .

Оскільки 0  m  n, то 0  PA1.

Операції над подіями. Сумою(об’єднанням)подій A та Β називається подія С , яка полягає в появі принаймні однієї з цих подій. Інакше кажучи, подія С полягає в настанні або події A, або події Β , або обох цих подій водночас. Суму подій позначають так:

C  A B або C  A B .

Добутком двох подій A та Β називається подія С , яка полягає в настанні як події A, так і події Β . Добуток подій позначають AB  С або A B  C . Очевидно, якщо події A й Β несумісні, то їхній добуток – неможливаподія: A B  .

Нехай імовірності подій A й B відомі й дорівнюють P(A) та

P(B) відповідно. Ймовірність суми несумісних подій знаходимо за теоремою додавання ймовірностей.

Теорема (додавання ймовірностей). Ймовірність настання суми двох несумісних подій дорівнює сумі ймовірностей цих подій, тобто

P A B P(A)  P(B) .

Дві події A та A називаються протилежними, якщо вони несумісні й утворюють повну групу подій.

Оскільки події A та A утворюють повну групу, то під час випробування одна з них обов’язково наступить, тобто сума

протилежних подій є вірогідна подія: A A U . Якщо ймовірність події A дорівнює p , то ймовірність протилежної їй події A дорівнює q 1 p . Очевидно, що для протилежних

подій A та A справедливі співвідношення: A та AA   та p  q 1.

Події A і B називаються незалежними, якщо ймовірність появи однієї з них не залежить від появи другої.

Теорема (множення ймовірностей). Ймовірність добутку двох незалежних подій A і B дорівнює добуткові їхніх імовірностей, тобто:

PA B PAPB. Повторні незалежні випробування. Формула Бернуллі. На практиці зустрічаються задачі, коли одне й те саме випробування повторюється багато разів. Якщо ймовірність появи події A в кожному випробуванні не залежить від результатів решти випробувань, то випробування називають незалежними щодо події A.

Схема Бернуллі – це серія незалежних випробувань, у кожному з яких можливі тільки два наслідки: подія A (успіх) або

протилежна подія A (невдача). Ймовірність появи події A не залежить від номера випробування і дорівнює p . Отже,

ймовірність непояви події A (тобто ймовірність появи події A) є сталою величиною в серії випробувань і дорівнює q 1 p .

Ймовірність того, що в n випробуваннях (за схемою Бернуллі) подія A настане рівно m разів, дорівнює

Pn(m)  Cnm pmqnm ,

де p – ймовірність появи події в одному випробуванні, а

q 1 p .

ЛІТЕРАТУРА

1. Математика. Навчальна програми для загальноосвітніх навчальних закладів. Програма затверджена Наказом Міністерства освіти і науки України від 07.06.2017 № 804.

https://mon.gov.ua/ua/osvita/zagalna -serednya -osvita/ navchalni -programi/

2. Державний стандарт базової і повної загальної середньої освіти. Затверджено постановою Кабінету Міністрів України від 23 листопада 2011 р. № 1392.

3. Васильків Г. І., Васильків І. М., Максимук О. В. Математика. Посібник для абітурієнтів. – Львів, 2005.

4. Васильків Г. І. Параметри на ЗНО та в олімпіадних завданнях. Навчально-методичний посібник. – Львів: НМЦО, 2016.

5. Васильків Г. І. Математика. Посібник для підготовки до ЗНО у 3-х частинах. – Львів: НМЦО, 2017.

6. Істер О. С., Єргіна О.В. Алгебра і початки аналізу. Підручник для 10-го класу закладів загальної середньої освіти. – К. «Генеза», 2018. – 447 с.

7. Істер О. С., Єргіна О.В. Алгебра і початки аналізу. Підручник для 11-го класу закладів загальної середньої освіти. – К. «Генеза», 2019. – 416 с.

8. Істер О. С., Єргіна О.В. Геометрія. Підручник для 10-го класу закладів загальної середньої освіти. – К. «Генеза», 2018. – 365 с.

9. Математика. Експрес підготовка до ЗНО. Нелін Є. П. – Київ: Літера, 2022. – 352 с.

10. Математика. Комплексна підготовка / Горох В. П. та ін.: Навч. посіб. – Харків: Факт, 2018. – 116 с.

11. Математика. Комплексна підготовка до зовнішнього незалежного оцінювання / Капіносов А. М. та ін. – Тернопіль: “Підручники і посібники”, 2020. – 527 с.

12. Погорєлов О. В. Геометрія: Підручник для 7 – 11 класів. – Київ: Освіта, 2001.

13. http://www.lvtest.org.ua

Навчальне видання