Визначення довжини кола

Довжина кола визначається за формулою: L = 2 * π * r, де L - довжина кола, π - математична константа приблизно рівна 3.14159, r - радіус кола.

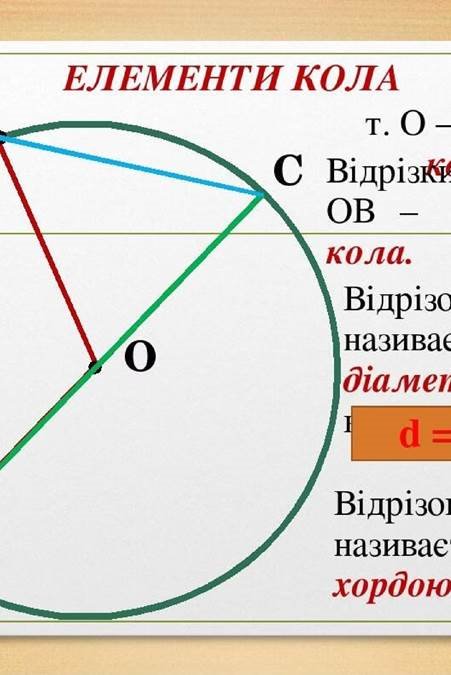
Радіус кола - відстань від центру кола до його будь-якої точки на околі. Довжина кола також може бути визначена за допомогою діаметра, в такому випадку формула виглядає так: L = π * d, де d - діаметр кола.

DA by Dmytro Yefimenko

Формула для обчислення довжини кола

Довжина кола визначається за формулою: L = 2 * π * r, де L - довжина кола, π - число Пі (близько 3.14159), r - радіус кола.

Ця формула є важливою при розв'язанні різних математичних завдань, пов'язаних з геометрією та фізикою. Вона також знадобиться при обчисленні маршрутів на карті або при розрахунку кількості матеріалу для виготовлення колового виробу.

Приклади обчислення довжини кола

десяткових знаків.

Визначення площі круга

Площа круга - це площа, обмежена колом. Вона визначається за формулою S = πr^2, де π (пі) - це математична константа, що приблизно дорівнює 3,14159, а r - радіус круга. Діаметр круга (d) також може бути використаний для обчислення площі, формула в цьому випадку виглядає так: S = 1/4πd^2. Ці формули дозволяють легко визначити площу будь-якого круга без великого зусилля або складних обчислень.

Формула для обчислення площі круга

Площа круга обчислюється за допомогою формули: S = πr², де S площа, r - радіус круга. Число π (пі) у формулі дорівнює близько 3,14. Для знаходження площі круга потрібно піднести радіус до квадрата і помножити на π.

Ця формула дозволяє швидко та просто обчислити площу круга будьякого розміру. Вона використовується в багатьох галузях, включаючи інженерію, архітектуру, та фізику. Розуміння цієї формули є ключовим елементом у вирішенні різноманітних завдань, пов'язаних з кругами та їх властивостями.

Приклади обчислення площі круга

                  Обчислення площі кола з радіусом 5 одиниць

Для цього обчислення використовуємо формулу S=πr², де r радіус. Підставляємо значення радіуса (5) в формулу: S=π*5². Отримуємо площу кола, яка дорівнює 25π квадратних одиниць.

2                       Обчислення площі кола з діаметром 10 одиниць

Якщо нам дано діаметр кола, то можна знайти радіус, розділивши діаметр на 2. Тоді, використовуючи ту ж формулу S=πr², вводимо значення радіуса (5) і обчислюємо площу як S=π*5², що дає нам 25π квадратних одиниць.

3                       Обчислення площі кола за допомогою довжини кола

Якщо відома довжина кола, то можна визначити його площу за формулою S=(C²)/(4π), де C - довжина кола. Приклад: якщо довжина кола дорівнює 10, то S= (10²)/(4π) ≈ 7.96 квадратних одиниць.

Формули для обчислення довжини та площі тайого елемента

Для обчислення довжини кола використовується формула: довжина = 2 * π * радіус. Де π (пі) - це математична константа, що приблизно дорівнює 3.14, а радіус - відстань від центру кола до його зовнішнього краю.

Що стосується площі круга, то формула для її обчислення така: площа = π * радіус^2. Тут π знову визначається як математична константа, а радіус - відстань від центру кола до будь-якої його точки.

Приклади обчислення довжини та площі тайого елемента

                                                                                                                                                         Обчислення довжини кола

Довжину кола можна обчислити за формулою: L = 2 * π * r, де L довжина кола, π - число пі, r - радіус кола.

3 Елементи та формули

2 Обчислення площі круга

Площу круга можна обчислити за формулою: S = π * r^2, де S - площа круга, π - число пі, r - радіус кола.

Довжина та площа тайого елемента пов'язані з радіусом кола та числом пі, які представлені формулами з точними відношеннями та розрахунками.

Застосування в реальному житті