"Екстремум функції" протовження вивчення теми

Алгебра 10 клас

Тема: Екстремальні точки. Локальний екстремум функції

Очікувані результати:

- ознайомитись  з правилами знаходження екст­ремумів функції.

- навчитись застосовують похідну для знаходження екстремумів функції,

розв’язувати завдання  на знаходження точок 

екстремуму та екстремумів функції

Для цього

потрібно

Додаток 1.  Опорний конспект  

 При дослідженні поведінки функ­ції в деякій точці зручно користува­тися поняттям околу.

Околом точки  а називається будь-який інтервал, що містить цю точку.

Наприклад, інтер­вали (2; 5),   (2,5; 3,5), (2,9; 3,1) – околи точки 3.

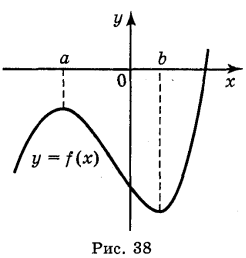
Розглянемо графік функції, зоб­ражений на рис. 38.

Як видно із ри­сунка, існує такий окіл точки x = а, що найбільше значення

функція у = f(x) в цьому околі набуває в точці х = а. Точку х = а називають точкою максимуму цієї функції.

Аналогічно точку х = b називають точкою мінімуму функції y = f(x), оскільки значення функції в цій точці найменше по­рівняно зі значеннями функції в деякому околі точки b.

Точки максимуму позначають х_max , а точки мінімуму — х_min.

Точки максимуму х_max і точки мінімуму х_min  - це точки екстремуму функції.

Значення функції в цих точках, тобто максимуми і мінімуми функції, позначаються відповідно: у_max і у_min і називають екстремумами  функції.

Для дослідження у = f(x) на точки екстремуму доцільно виконувати наступну схему:

1) Знаходимо область визначення функції у = f (х).

2) Знаходимо похідну f '(x). (таблиця похідних ст.. 185, правила ст..181 підручника)

3) Знаходимо критичні точки та розв’язки рівняння f '(х) = 0. (тобто прирівнюємо похідну до нуля та розв’язуємо утворене рівняння)

4) Позначаємо знайдені точки на області визначення функції у = f(х) та знаходимо знак похідної f '(х) у кожному з цих проміжків (робимо зображення проміжку та позначаємо на ньому точки знайдені в  пункті 3,  визначаємо знак похідної f'(x) в якійсь одній «пробній» точці проміжку )

5) Якщо у критичній точці х₀ похідна міняє

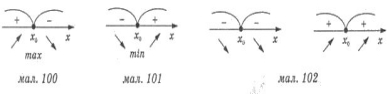знак з «+» на «-», то х₀= х_mах (мал. 100).

Якщо ж міняє знак з «-» на «+»,

то х₀ = х_min (мал. 101).

Якщо ж зміни знаків немає (мал. 102),

то х₀ не є точкою екстремуму.

6) Робимо висновок (відповідь).

7) Якщо ж потрібно знайти екстремум функції, тоді значення

х_min та х_mах  підставляємо в вираз умови і рахуємо у_max і у_min

Приклад:  Знайдіть екстремуми функції  f(x)= 3х⁵ - 5x³ + 1.

Розв'язання

1.Область визначення функції — R.

2.Знайдемо похідну:   f ^‘(x) = 15х⁴ – 15х² = 15х² (х²  - 1) =15х² (х  - 1)(х + 1)

3. Знайдемо критичні точки: 15х² (х  - 1)(х + 1) = 0

                                                  х₁ = 0, х₂ = - 1,  х₃ = 1

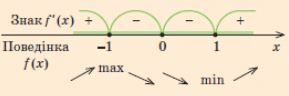4. Наносимо критичні  точки на координатну пряму  та визначаємо знак похідної на кожному інтервалі. 

 х _min = 1 — точка мінімуму,

(бо при переході через цю точку

похідна змінює знак з «-» на «+»:) 

х _mах = -1 – точка максимуму.

(бо при переході через цю точку  похідна змінює знак з «-» на «+») 

Точка х = 0 не є точкою екстремуму, бо похідна не змінює знак при переході через цю точку.

Отже, знаходимо екстремум функції

у _min =f (1) = 3 * 1⁵ – 5 ·1³  + 1 = - 1.          у _mах =f (-1) =3 * (-1)⁵ – 5 ·(-1)³  + 1 = 3.            

Відповідь: у _min = f (1) = -1         у _mах =f (-1) = 3