Елементи комбінаторики

 Елементи комбінаторики

Щоб обчислити ймовірність тієї чи іншої випадкової події для певного класу задач із дискретним і обмеженим простором елементарних подій, необхідно вміти обчислити кількість усіх елементарних подій (елементів множини) і числоелементарних подій, які сприяють появі випадкової події.

Існує клас задач, в яких для обчислення використовуються елементи комбінаторики: переставлення, розміщення та комбінації. У комбінаториці оперують множинами однотипних елементів.

Загалом множини бувають упорядковані та невпорядковані.

Множину називають упорядкованою, якщо при її побудові істотним є порядок розміщення елементів. У противному разі множину називають невпорядкованою.

Переставлення. Переставленнями із елементів називають такі впорядковані множини зелементів, які різняться між собою порядком їх розміщення.

Кількість таких упорядкованих множин обчислюється за формулою

, (2.2)

де набуває лише цілих невід'ємних значень.

Приймають, що 1! =1 і 0!=1.

Приклад 1. Задано множину цілих чисел = {1, 2, 3, 4, 5}. її елементи навмання розставляють у рядок. Обчислити ймовірності таких випадкових подій:

А — розставлені в ряд числа утворюють зростаючу послідовність;

В — спадну послідовність;

С — цифра 1 стоятиме на першому місці, а 5 — на останньому;

Розв'язання. Простір елементарних подій для цього експерименту міститиме =5!=1·2·3·4·5=120 несумісних, рівноможливих елементарних подій.

Кількість елементарних подій, що сприяють появі А дорівнює одиниці (= 1). Кількість елементарних подій, що сприяють появі В дорівнює одиниці (= 1). Для випадкової події С= 3!. Тоді

.

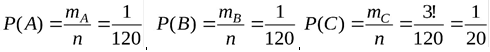Розміщення. Розміщеннями із n елементів по m (0 < m < n) називаються такі впорядковані множини, кожна з яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом.

Кількість таких множин обчислюється за формулою

. (2.3)

Наприклад, = 9 ·8 ·7 = 504 .

Комбінації. Комбінаціями з n елементів по m (0 < m < n) називаються такі множини з m елементів, які різняться між собою хоча б одним елементом. Кількість таких множин

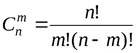. (2.4)