1. Лінійні рівняння та рівняння, що зводяться до лінійних.

Рівняння виду axb0, де a і b - деякі вирази, що залежать лише від параметрів, а x - невідома змінна, називається лінійним рівнянням. Це рівняння зводиться до вигляду ax  bі при a  0 має єдиний розв’язок b

x при  кожній допустимій системі значень параметрів. При a  0 і a

b  0 розв’язком рівняння є будь-яке число, а при a  0, b  0 рівняння

розв’язків не має.

В більшості завдань, які будуть  розглянуті в наступних пунктах, потрібно буде визначити  „ при яких значеннях параметра ...? ”. Подібне питання для рівнянь, нерівностей, систем рівнянь або нерівностей з параметром не завжди фігурує в умові завдання. Однак наявність параметра зразу припускає спеціальну форму запису відповіді, таку, щоб по ній можна було вказати, якою буде відповідь для будь-якого допустимого значення параметра.

Завдання 1. Розв’язати  рівняння a²x 1 x  a, де a - параметр.

                Перепишемо    це    рівняння                      : a²xxa1, x(a² 1)a1,

1

x(a1)(a1) a1. Якщо a 1, то x. Якщо a1, то x - довільне a1

число, тобто рівняння має безліч розв’язків. Якщо a  1, то отримуємо

0  2, що неправильно ні при якому x, тобто рівняння розв’язків не має.

Завдання 2. При якому параметрі   а рівняння 2аа 2ха 2 має безліч розв’язків?

Розглянемо передусім ті значення параметра а, при яких коефіцієнт біля хперетворюється в 0. Такими значеннями є  а  0 і а  2. При а  0 рівняння набуває вигляду 0 х  2. Це рівняння не має коренів. При а  2 рівняння буде 0 х  0, його коренем буде будь-яке дійсне число. При

а  0 і а  2 рівняння можна звести до вигляду х_ ^а2 , звідки х_ ¹

                                                                                                                                                2а(а2)                      2а

. Отже рівняння має безліч розв’язків при а  2.

Завдання 3. Вказати при яких значеннях параметра а рівняння не матиме розв’язків  2(a 2x) ax 3. 

Перетворимо рівняння, розкривши дужки і погрупувавши доданки  2a4xax30, x(4 a)  (2a 3)  0.  Це рівняння не має розв’язків при  а=-4.

                Завдання 4. Розв’язати  рівняння                      , де a - параметр.

3xa x1

Область допустимих значень (ОДЗ)       3x  a,  x 1. Маємо x 1 6x  2a, 5x2a1, x. Перевіримо ОДЗ: 

1) 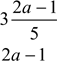   a, 6a  3  5a, a  3.

2)    a , 2a 1 5, a  3.

5

Отже x при a  3 і рівняння не має розв’язків при a  3.

Завдання 5.              

 При якому значенні параметра b пряма y  3x  bпроходить через точку А (-1,5) ? 

Підставимо координати точки А (-1,5) замість х і у в рівняння прямої. Отримаємо рівняння відносно b:  5  3(1)  b. Звідси  b=8

Завдання 6. Вказати при яких значеннях параметра а рівняння не матимуть розв’язків:

1)     x^{ 5} = ^ax . Відповідь: а=-19 x 7 x 7

8 ^{ 5x}

2)      2a. Відповідь: а=-2,5

2 x

3)     a²xa(x 2)  2. Відповідь: а=0

Завдання 7. При якому значенні параметра а пряма y  ax  3

проходить через точку А ( -2,9) ? Відповідь: а=-6

Завдання 8. При якому значенні параметра а рівняння ax43x має корінь, що дорівнює 8 ? Відповідь: а=3,5

Завдання 9. Розв’язати рівняння з параметрами:

1.)    x^{ 3} _ ^ax  Відповідь: x_^a3, якщо a 13; x, якщо  a 13 x 5 x 5.        2

.

                               2           1

2.)            Відповідь: x, якщо a  4; x(-, 2)(2, ), 2xa x 2. якщо a  4.

3   2x     6a 3 2

3.) 3a. Відповідь: x, якщо a; x, якщо 

2 x       3a 2 3 a.

Завдання 10.  Розв’язати рівняння при всіх допустимих значеннях параметра

1.) 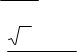      ax  2x  3 1 x.      Відповідь: x_ ^{ 2} ,  якщо a  3. a 3

2.) 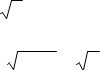      40x13a a15x.  Відповідь: x_ a^13a ,  якщо a  0. 25

a^{2 a12a}

3.)       40x12a a2 a36x.  Відповідь: x_,

4

якщо a  2.

4.)       3x  9  a(a  x).  Відповідь: xR, якщо a  3,  x  a  3, якщо a  3.