Урок "Способи інтегрування"
План відкритого заняття з математики «Способи інтегрування: заміною змінної, інтегрування частинами. Інтегрування деяких тригонометричних функцій»
Вид заняття: Лекційно - практичне
Дисципліна: Математика
Тема заняття: Способи інтегрування: заміною змінної; інтегрування
частинами; інтегрування деяких тригонометричних функцій.
Мета заняття:
Навчальна: Ознайомити студентів з різними способами інтегрування.
Навчити їх обчислювати невизначені інтеграли цими способами.
Розвиваюча: Формувати вміння виступати перед аудиторією; чітко
формулювати і відстоювати свою думку; розвивати
спостережливість, логічне мислення, інтелектуальні
здібності студентів; сприяти розширенню їх кругозору.
Розвивати пізнавальний інтерес та навики колективної
праці.
Виховна: Виховувати у студентів працелюбність, зібраність,
організованість, вимогливість до себе. Сприяти вихованню
самостійності студентів і їх математичної культури.
Мета відкритого заняття: Показати методику проведення лекційно – практичного заняття з математики з використанням інформаційно – комп’ютерних технологій.
Тип заняття: Повідомлення і засвоєння нових знань, формування вмінь і навичок
Методи: Дослідницький, проблемно – пошуковий, творчо - продуктивний, пояснювально – ілюстративний.
Матеріально-технічне забезпечення заняття:
комп’ютер, мультимедійний проектор, презентації до заняття
Навчальне місце (аудиторія чи лабораторія): аудиторія №307
Література (основна):
1.А.Г.Мерзляк, Д.А.Номіровський «Алгебра 11 клас», Харків «Гімназія», 2011р, §5, п.19, п.20.
2. М.І.Шкіль, З.І.Слєпкань «Алгебра і початки аналізу 10-11 кл », Київ «Зодіак - Еко», 1995р, розділ 9, §1-§4.
3. М.В.Богомолов «Практичні заняття з математики», Київ вид. «Вища школа», 1993 р, розділ 10, §3,§4, §6.
Література (додаткова):
1. Є. П. Нелін «Алгебра і початки аналізу 11 кл», Харків вид. «Світ дитинства»,
2006 р, розділ 2, §14; §15.
Структура і хід заняття
1. Організаційна частина
Привітання, перевірка наявності і підготовки студентів до заняття
Налаштування психоемоційного настрою студентів
2. Актуалізація опорних знань студентів і мотивація навчальної діяльності
Запитання до студентів
- Дати означення первісної та невизначеного інтеграла.
- Сформулювати властивості невизначеного інтеграла.
- Таблиця невизначених інтегралів.
- Поняття похідної, геометричний і фізичний зміст.
- Таблиця похідних основних елементарних функцій.
- Основні формули диференціювання.
- Визначений інтеграл та його властивості (повторення).
- Обчислення визначеного інтегралу. Формула Ньютона – Лейбніца.
3. Повідомлення теми, мети, змісту і послідовності вивчення нового матеріалу
Тема заняття: Способи інтегрування: заміною змінної; інтегрування частинами; інтегрування деяких тригонометричних функцій
- Інтегрування методом заміни змінної (спосіб підстановки)
- Інтегрування частинами
- Інтегрування деяких тригонометричних функцій
4. Узагальнення і систематизація знань і вмінь
Узагальнення і закріплення матеріалу, шляхом захисту міні-проектів
на тему «Застосування визначеного інтегралу в прикладних задачах»,
підготовлених студентами групи.
5. Підсумки заняття студентів
Підведення підсумків заняття. Аналіз загальної активності студентів, шляхом рефлексії.
6. Домашнє завдання
1. М.І.Шкіль, З.І.Слєпкань «Алгебра і початки аналізу 10-11 кл », Київ «Зодіак-Еко», 1995р, розділ 9, §4, стр.376, №10 (1-8)
2. М.В.Богомолов «Практичні заняття з математики», Київ вид. «Вища школа»,
1983 р, розділ 10, §3, стр.184, №112; №123
Пояснення нового матеріалу
Інтегрування методом заміни змінної
Суть інтегрування методом заміни змінної (способом підстановки) полягає в перетворенні інтеграла ![]() в інтеграл
в інтеграл ![]() , який легко обчислюється за будь-якою з основних формул інтегрування.
, який легко обчислюється за будь-якою з основних формул інтегрування.
Для знаходження інтеграла ![]() замінюємо змінну х новою змінною t за допомогою підстановки
замінюємо змінну х новою змінною t за допомогою підстановки ![]() . Диференціюючи цю рівність, дістанемо
. Диференціюючи цю рівність, дістанемо ![]() . Підставляючи в підінтегральний вираз замість
. Підставляючи в підінтегральний вираз замість ![]() їх значення виражені через
їх значення виражені через ![]() , маємо:
, маємо:
![]()
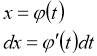
Коли інтеграл відносно нової змінної t буде знайдено, за допомогою підстановки ![]() його зводять до змінної x.
його зводять до змінної x.
Приклад 1
Знайдіть інтеграли способом підстановки
1)![]()
Розв’язання

2) ![]()
Розв’язання

3) 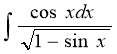
Розв’язання:

4) 
Розв’язання:

5)![]()

Розв’язання:
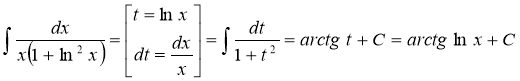
6) 
Розв’язання:

7) 
Розв’язання:

Інтегрування частинами
Інтегруючи обидві частини рівності ![]()
![]() , дістанемо
, дістанемо
![]()
![]()
![]()
За допомогою цієї формули обчислення інтеграла ![]() зводиться до обчислення інтеграла
зводиться до обчислення інтеграла ![]() , якщо останній буде простіший за вихідний.
, якщо останній буде простіший за вихідний.
Приклад 2
Знайдіть інтеграли методом інтегрування частинами
1) ![]()
Розв’язання:

2)![]()
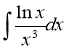
Розв’язання:

3) ![]()
Розв’язання:
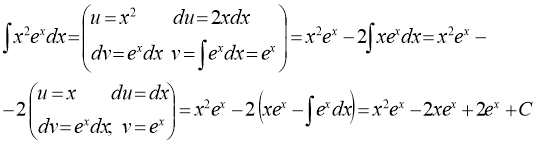
4) 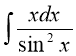
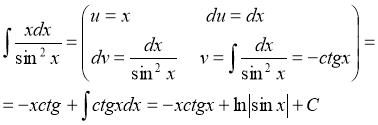
5) ![]()
Розв’язання:

Інтегрування деяких тригонометричних функцій
При обчисленні інтегралів вигляду ![]() або
або ![]() від парного степеня синуса або косинуса використовують формули зниження степеня:
від парного степеня синуса або косинуса використовують формули зниження степеня:
![]()
![]()
При обчисленні інтегралів вигляду ![]() або
або ![]() від непарного степеня синуса або косинуса треба відокремити від непарного степеня один множник і ввести нову змінну, вважаючи t=cosx в першому випадку і t=sinx у другому випадку.
від непарного степеня синуса або косинуса треба відокремити від непарного степеня один множник і ввести нову змінну, вважаючи t=cosx в першому випадку і t=sinx у другому випадку.
Приклад 3
Знайдіть інтеграли:
-
 ;
;
-
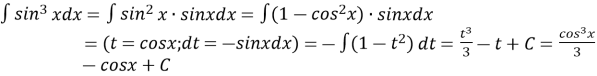 ;
;
-
 .
.


про публікацію авторської розробки
Додати розробку
