EXCEL. ЗНАХОДЖЕННЯ КОРЕНІВ ФУНКЦІЇ

          Задача. Задана довільна функція y(x). Треба знайти всі її корені на заданому відрізку 𝑥 ∈ [𝑎, 𝑏].

          З математики відомо, що для знаходження коренів функції треба вирішити рівняння 𝑦(𝑥) = 0. Аналітичне рішення вдається отримати далеко не для кожної функції. Рівняння, для яких не можна знайти аналітичні рішення, називаються трансцендентними. Для находження коренів трансцендентних рівнянь застосовуються графічні або чисельні методи.

          Слід відмітити, що графічний спосіб знаходить всі корені на заданому відрізку, але їх значення, як правило, є дуже неточними. Чисельні методи знаходять корені з великою точністю, але самі методи розраховані на пошук лише одного кореня на заданому відрізку, де заздалегідь відомо, що функція монотонна і має лише один корінь. Тож для знаходження всіх коренів на заданому відрізку можна спочатку графічним методом знайти всі корені приблизно, а потім за допомогою одного з чисельних методів уточнити ці значення для кожного кореня.

 В роботі розглянуто, як в Excel реалізується графічний метод пошуку всіх коренів функції на заданому відрізку та їх уточнення за допомогою функції "Підбір параметра".

          Як приклад, розглянемо знаходження коренів функції  𝑦 = 2𝑥⁴ + 4𝑥 − 10000 на інтервалі 𝑥 ∈ [−10, 10].

Графічний метод

1.     Для побудови графіка створимо таблицю значень функції y2x⁴ 4x10000 на інтервалі x10;10. Кількість точок рекомендується не менше, ніж 15-20. По даним таблиці побудуємо графік функції (Рис. 1)

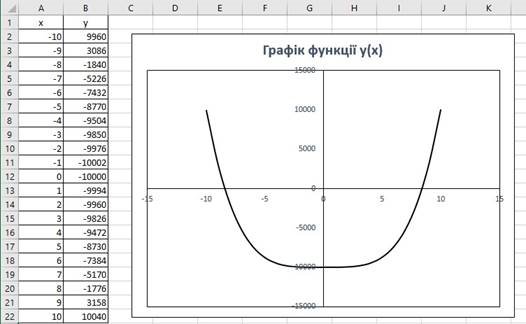
Рис. 1. Графік функції

2.     Із графіка приблизно визначимо корні функції y(x) (корні функції знаходяться в точках перетину графіка функції з віссю х). В даному графічно корні функції можна приблизно визначити як х₁=-8 та х₂=8.

          Як бачимо задана функція має два корені. Знайдені графічним способом вони мають приблизні значення, які потрібно уточнити чисельним методом.            В Excel існує два таких методи: підбір параметру і пошук рішення. Нижче розглянемо застування першого з них – методу підбору параметру

Уточнення знайдених коренів

1.     За допомогою інструмента Подбор параметра (Данные Анализ "что если"  Подбор параметра…) спочатку уточним перший корінь функції:

2

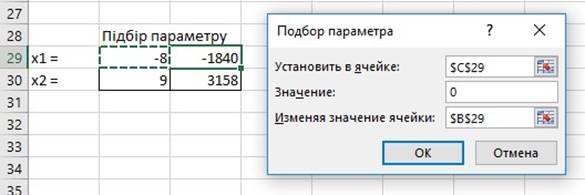
Рис. 2. Функція Підбір параметру для знаходження першого кореня

2.     Аналогічно уточнимо значення другого кореня.

3.     У результаті маємо:

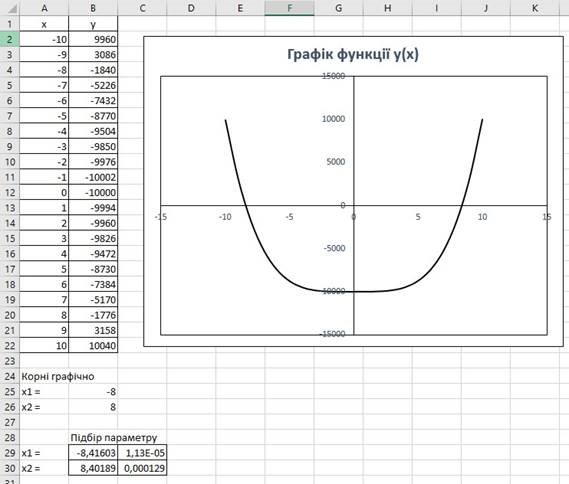
3