Фалес Мілетський і давньогрецька наука
Про матеріал
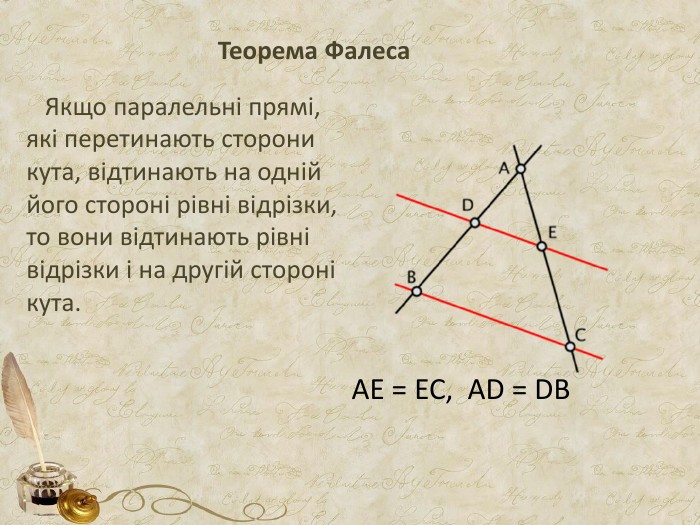
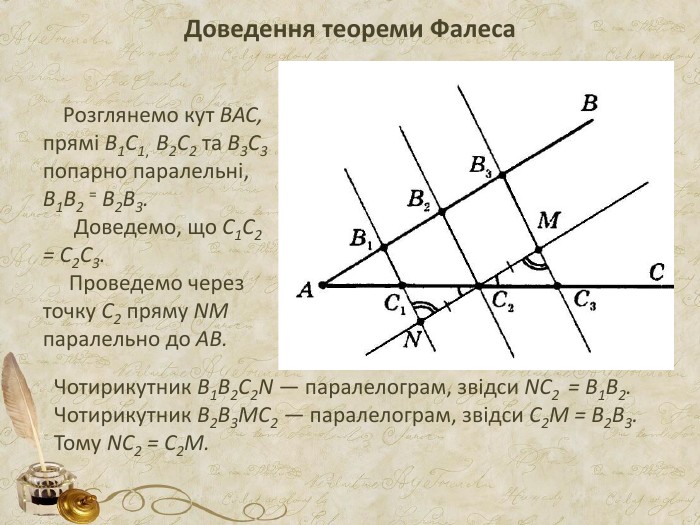
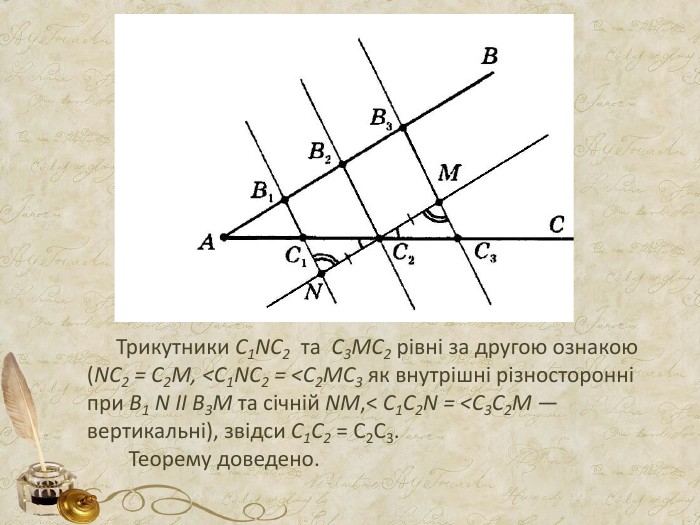
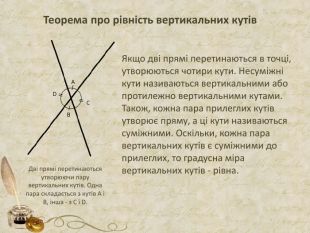
Презентація може бути використана як додатковий матеріал на уроках геометрії Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку