Фальшиві задачі. До уроку

БЗШ № 3 ім. Т.Г.Шевченка

А.І. Сахненко

м. Біла Церква

З давніх-давен математика була й залишається актуальною наукою, адже серед усіх наук, що відкривають людству шлях до пізнання законів природи, вона є наймогутнішою.

Відомий американський математик, основоположник кібернетики Норберт Вінер зазначав: «Математика – наука молодих, інакше й не може бути, бо заняття математикою – це така гімнастика розуму, для якої потрібна вся гнучкість і вся витривалість молодості». Тому багато випускників намагається пов’язати свою майбутню професію з царицею усіх наук – математикою.

 Нині, в епоху розвитку інформаційних технологій, молодь має доступ до будь-якої інформації. Для саморозвитку це має колосальне значення, проте нерідко виникають ситуації, коли учні під час розв’язування  задач потрапляють в умови невизначеності, а саме: задачі не мають розв’язків або запропоновані розв’язки є невірними. Наведемо приклади:

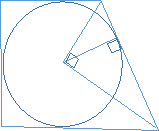
Задача 1. У прямокутну трапецію вписано коло. Точка дотику ділить більшу бічну сторону на відрізки 6 і 14 см (рахуючи від вершини тупого кута). Знайти площу трапеції, якщо її периметр дорівнює 66 см.

Розв’язання

      B                        C                                                       

                                                   P           

                      O                     

        A                                   D

І-й спосіб

Нехай трапеція ABCD (<А=90°) описана навколо кола. Точка дотику Р ділить бічну сторону CD на відрізки СР = 6 см і РD = 14 см.

Оскільки трапеція описана, то АD + ВС = 33 см

СD = 20 см, тоді АВ = 33 -  20 = 13 см

Sтрап. = ∙АВ;

Sтрап. = ∙ 13 = 214,5 см

ІІ-й спосіб

В трикутнику СОD (<О=90°) проведемо радіус ОР у точку дотику Р.

З трикутника СОD слідує OP² = CP ∙ PD

ОР = = 2 см, тоді

АВ = 2ОР = 4 см

Тоді АВ + СD = 20 + 4 ≠ 33 см. Чому?

Оскільки трапеція прямокутна і описана навколо кола, то периметр трапеції є зайвою величиною. В даній задачі коло не є  вписаним у трапецію. Формулювання задачі не вірне.

Задача 2. Сума діагоналей ромба дорівнює 16 см, а сторона дорівнює 5 см. Знайти площу ромба.

Розв’язання

 Наведемо приклад авторського розв’язання.

Нехай d₁ і d₂ діагоналі ромба, його сторона а = 5 см. За умовою d₁ + d₂ = 16 см

(d₁ + d₂)² = d₁² + 2 d₁d₂ + d₂²;

d₁² + 2 d₁d₂ + d₂² = 256;

d₁² + + d₂² = 64.

Діагоналі ромба перпендикулярні, тому:

( d₁)² + d₂)² = а²;

d₁ ∙ d₂ + 25 = 64;

d₁∙d₂ = 39;

S_ромба = d₁ ∙ d₂ = 39 см²

Пропоную інший варіант розв’язку. Нехай  d₁ = Х см, тоді d₂ = (8 – х) см.

Оскільки ( d₁)² + d₂)² = а², то маємо рівняння :

х² + (8 – х)² = 25

2х² – 16х + 39 = 0

= 64 - 78 = -14  Рівняння коренів немає, а тому такого ромба не існує.

Задача розв’язків не має. Це тому, що при складанні задачі не було враховано існування прямокутного трикутника при відповідних даних.

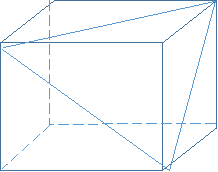
Задача 3. У прямокутному паралелепіпеді діагоналі трьох різних граней дорівнюють 10, 5 і 7 см. Знайти виміри паралелепіпеда.

Розв’язання

      B₁                                                    C₁ 

      A₁                                     D₁    

                    B                                 C

      А                                       D

Нехай у прямокутному паралелепіпеді ABCDA₁B₁C₁D₁   A₁C₁ = 10см,              A₁D = 5, C₁D = 7 Приймаємо виміри паралелепіпеда за x, y, z см.

Згідно умови складаємо систему рівнянь:

    x² + y² = 100

    x² + z² = 325

    y² + z² = 539

Додаємо рівняння

2(х² + y² + z²) = 964

х² + y² + z² = 482

Оскільки x² + y² = 100, то z² = 382.

З другого рівняння x² = - 57. Задача розв’язків не має. Чому? Тому, що умову задачі складено невірно.

Трикутник A₁C₁D зі сторонами 10 см, 5 і 7 існує, бо навіть найбільша сторона 7< 10 + 5. Отже, прямокутного паралелепіпеда не існує. Перевіримо чи при вихідних даних  існує прямий паралелепіпед.

Нехай A₁C₁ = 7см, тоді з трикутника A₁C₁D₁ (< D₁ = α) маємо:

x² + y² – 2 x y cosα = 539

Розв’яжемо систему:

       x² + y² – 2 x y cosα = 539

       x² + z² = 325

       y² + z² = 100

Або:

       x² + y² – 2 x y cosα = 539

       x² - y² = 225

Додаємо рівняння системи:

2x² – 2 y cosα∙ х = 764

2x² – 2 y cosα∙ х – 764 = 0

= y² cos²α + 1528

Очевидно, що нас задовольняє корінь

х =

Якщо α та y змінюються, то х також набуває різних значень в певному «коридорі», інакше тоді система не матиме розв’язків.

Для прикладу, нехай х = 17 см, тоді :

 = 34

Замінюємо y cos α на t. Маємо : = 34 – t, або  68 t = - 382,

t = - 5 . Оскільки |cos α| ≤ 1, то нехай y = 8 см, тоді cosα ≈ - 0,6838, а α ≈ ≈133°.

З другого і третього рівнянь системи знайдемо х та z;  х = 17 см, z = 6 см.

Отже, існує безліч прямих паралелепіпедів, в яких діагоналі граней мають вказані довжини, а прямокутного паралелепіпеда не існує.