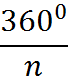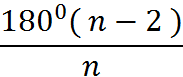Формули радіусів вписаних і описаних кіл правильних многокутників.

Урок №2

Тема уроку                Формули радіусів вписаних і описаних кіл

             правильних многокутників.

 

Мета уроку. Узагальнити поняття правильного многокутника та його

              елементів, ввести поняття правильного многокутника, попередньо

              повторивши і узагальнивши матеріал про многокутники,   

               допомогти учням оволодіти основними поняттями теми;

             розвиток  життєвих компетентностей, інтелекту учнів, уміння

               аналізувати, класифікувати, порівнювати, робити умовиводи;

               виховувати математичну культуру, звичку до систематичної

               розумової праці, позитивне ставлення учнів до навчально-

               пізнавальної діяльності, радість від отриманих результатів.

Наочність та обладнання.

             Таблиця «Формули радіусів вписаних і описаних кіл

             правильних многокутників», ноутбук, проектор,

             геометричні прилади

 

 

Тип уроку. Комбінований з використанням елементів інтерактивних

                    технологій.

 

Хід уроку.

Вітання. Ознайомлення з темою уроку та епіграфом ( на дошці ):

 

 

 

 

 

 

 

1. Перевірка домашнього завдання

 ( с. 50 - 53)

                                      Вик. № 224 (2), 228 (1).

Математичний диктант (закінчити  речення):

 

1. Опуклий многокутник у якого всі сторони рівні і всі кути рівні називається правильним.
2. Градусна міра кута правильного многокутника залежить від кількості сторін ( вершин, n)
3. Центральним кутом правильного многокутника називається кут, утворений двома  радіусами, проведеними у сусідні вершини.
4. Його величина обчислюється за формулою 360⁰/n .
5. Правильний трикутник – це трикутник, у якого всі сторони і кути рівні.
6. Його внутрішній кут дорівнює 60⁰ , а зовнішній  - 120⁰.
7. Правильний чотирикутник  називається квадратом.
8. Перпендикуляр, опущений з центра правильного многокутника до його сторони, називається апофемою.
9. Кожен внутрішній кут правильного шестикутника має величину 120⁰.

10. У правильному многокутнику центри вписаного і описаного кіл співпадають

11.Сума зовнішніх кутів правильного многокутника дорівнює 360⁰.

12. Для знаходження міри кута правильного многокутника використовують формулу 1800*( n-2 )/n

 

Самоперевірка :

 ( таблиця спроектована на дошку) і занесення результатів у бланки оцінювання.

2. Узагальнення і систематизація знань. Основні типи задач і алгоритми їх розв’язування.

Висновок 1.

Якщо сума  зовнішніх кутів правильного многокутника 360⁰, то

         величина кожного зовнішнього кута – 360⁰ / n, 

                                а внутрішнього – 180⁰ – 360⁰ / n

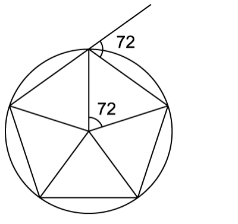
Величини зовнішнього куту правильного многокутника та його центрального кута РІВНІ.  

Приклади задач:

• Знайти величини зовнішнього і внутрішнього кутів правильних опуклих : 8, 9, 12, 24, 60-кутників.

Висновок 2.

             Якщо сума градусних мір внутрішніх кутів правильного

             опуклого многокутника 180⁰ ( n - 2 ),  то

             величина кожного внутрішнього кута – 180⁰ ( n - 2 ) / n,

             а величина зовнішнього кута – 180⁰ – внутрішній кут.

Приклади задач:

• Знайти величини зовнішнього і внутрішнього кутів правильних опуклих : 8, 9, 12, 24, 60-кутників.

    - Чи існує правильний многокутник, кут якого дорівнює:

1) 177⁰;            2) 155⁰ ?

      У випадку позитивної відповіді вкажіть вид многокутника.

Розв’язання.

1) Нехай n — кількість сторін шуканого правильного многокутника. Тоді сума його кутів дорівнює 180⁰(n – 2) або 177n. Отже,

180(n – 2) = 177n;    180n – 360 = 177n;    n = 120.

Відповідь: Існує, це стодвадцятикутник.

2) Маємо: 180(n – 2) = 155n; 25n = 360; n = 14,4, що неможливо, оскільки n має бути натуральним числом.

Відповідь: Не існує.

Вивчення та осмислення нового матеріалу.

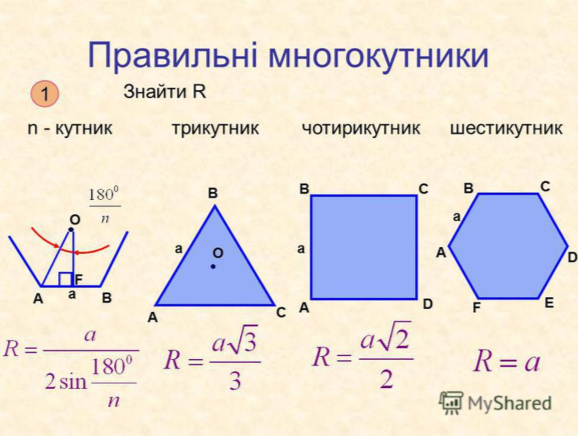
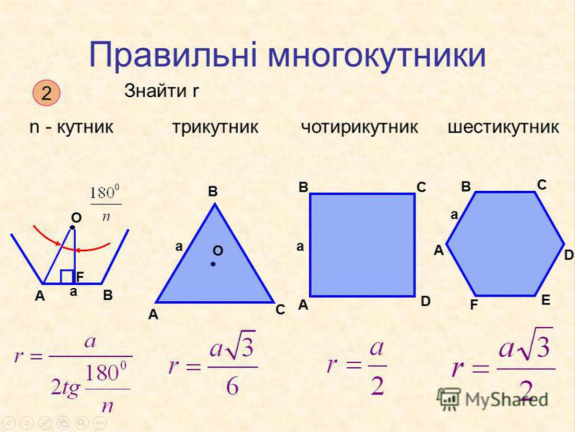
На рисунку зображено фрагмент правильного n-кутника з центром O і стороною AB, довжину якої позначимо a_n.

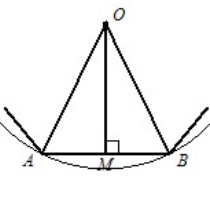
Кут AOB - центральний кутом правильного многокутника.

Зрозуміло, що AOB = 360⁰ / n.

У рівнобедреному трикутнику AOB проведемо висоту OM. ( ОМ – апофема многкутника ). Тоді

AOM =  BOM = , AM = MB = . З OMB

                     .

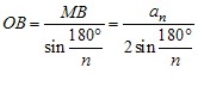
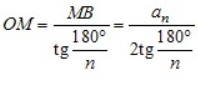Відрізки OB і OM — радіуси описаного і вписаного кіл правильного n-кутника. Якщо їх довжини позначити R і r відповідно, то отримані результати можна записати у вигляді формул:

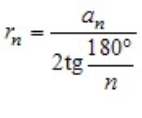
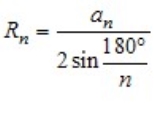
П          Перегляд презентації  ( Слайди 1- 6 )

Складання друк і роздавання учням таблиці залежностей між стороною та радіусами вписаного і описаного кіл правильних опуклих многокутників.

n	a		r		R
	R  --- > a	r  --- > a	a  --- > r	R  --- > r	a  --- > R	r  --- > R
3	a = R	a = 2r	r = =	r =	R = =	R = 2 r
4	a = R	a = 2r	r =	r =	R =	R = r
6	a = R	a = =	r =	r =	R = a	R = =

 

Підсумок уроку 

 

Математичний диктант

( Відповіді )

 

Номер  запитання	Відповідь
1	Правильним
2	Сторін ( вершин, n)
3	Сусідні вершини
4
5	всі сторони і кути рівні
6	600 , а зовнішній  - 1200
7	Квадратом
8	Апофемою
9	1200
10	Співпадають
11	3600
12

 

Додаткові матеріали

 

Про правильні n-кутники

Доведемо, що будь-який правильний n-кутник є опуклим многокутником.

Для цього достатньо показати, що в будь-якому многокутнику є хоча б один кут, менший від 180. Тоді з того, що в правильному n-кутнику всі кути рівні, випливатиме, що всі вони менші від 180, тобто многокутник буде опуклим.

 Ви вмієте за допомогою циркуля і лінійки будувати правильний 4-кутник, а отже, й 8-кутник, 16-кутник, 32-кутник, тобто будь-який 2ⁿ-кутник (n — натуральне, n > 1).

Уміння побудувати правильний трикутник дає змогу побудувати такий ланцюжок з правильних многокутників: 6-кутник, 12-кутник, 24-кутник і т.д., тобто будь-який 3  2ⁿ-кутник (n — натуральне).

Задача побудови правильних многокутників за допомогою циркуля і лінійки вивчалася ще давньогрецькими геометрами. Зокрема, крім зазначених вище многокутників, вони вміли будувати правильні 5-кутник і 15-кутник, що є досить непростою справою.

Зрозуміло, що стародавні вчені, які вміли будувати будь-який з правильних n-кутників, де n = 3, 4, 5, 6, 8, 10, намагалися розв’язати цю задачу і для n = 7, 9. Їм це не вдалося. Взагалі, більше двох тисяч років ніхто не міг досягти результату в розв’язанні цієї проблеми. Лише в 1796 р. великий німецький математик Карл Фрідріх Гаусс (1777 — 1855) зміг довести, що циркулем і лінійкою побудувати правильні 7-кутник і 9-кутник неможливо.

У 1801 р. Гаусс показав, що циркулем і лінійкою можуть бути побудовані лише ті правильні n-кутники з непарною кількістю сторін, для яких число n є простим числом виду  або добутком кількох таких різних чисел, які називають числами Ферма (Пьер Ферма (1601 – 1665) — французький математик, один з фундаторів теорії чисел). Зараз відомо лише п’ять простих чисел Ферма: 3, 5, 17, 257, 65537.

Гауссу вдалося побудувати правильний 17-кутник. Він надавав цьому відкриттю настільки великого значення, що заповідав увіковічити 17-кутник на його надгробку. На могильній плиті Гаусса цього рисунку немає, проте сам пам’ятник стоїть на сімнадцятикутному постаменті.

 

 

  Бджолині соти складаються з шестигранних воскових ячейок , які вкладені у два шари, що дотикаються днищами. Бджоли дуже розумні, вони обрали шестигранну форму тому, що намагались якомога економніше використати площу в середині невеликого вулика і вибрали ту фігуру, якою можна без накладань і прогалин заповнити площину, яка при однаковій площі має найменший периметр. Мабуть, рішення цієї задачі їм підказав інстинкт.

 

   Якщо ми побажаємо загородити ділянку певної площі так, щоб на загороду пішло як найменше матеріалу, то їй слід придати форму правильного шестикутника.

Презентація 1

 

 

 

 

 

Презентація 2