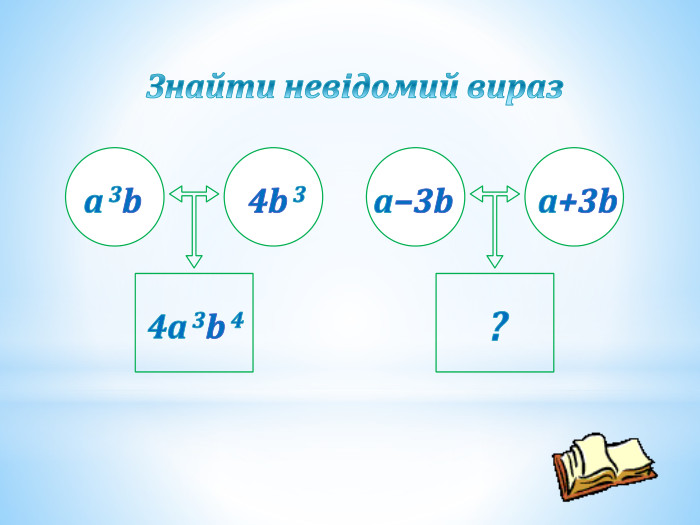
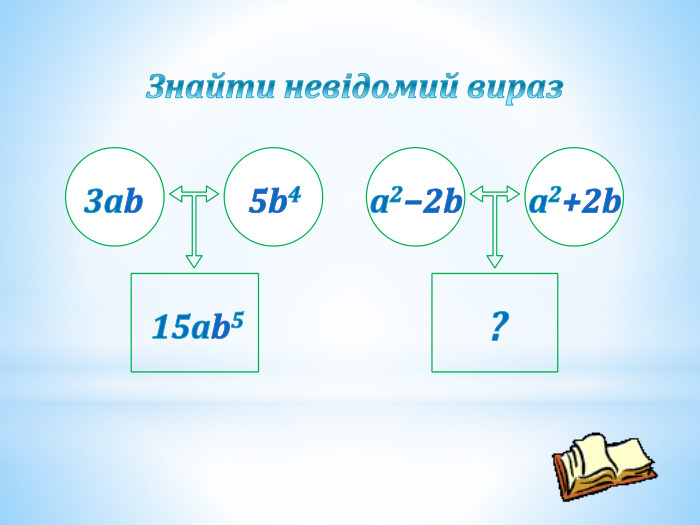
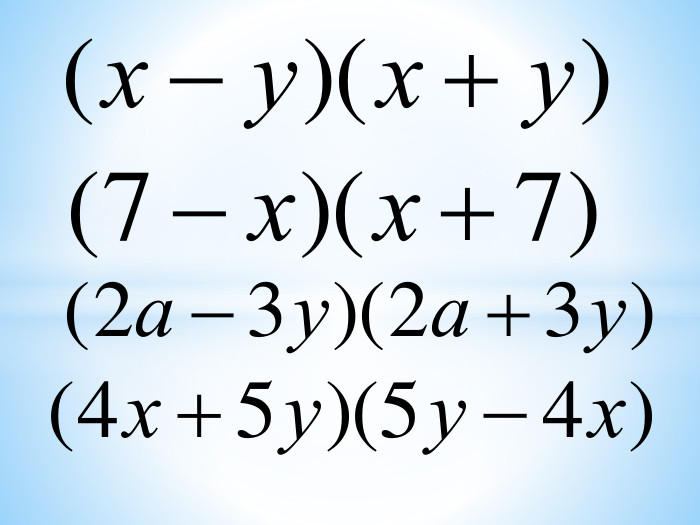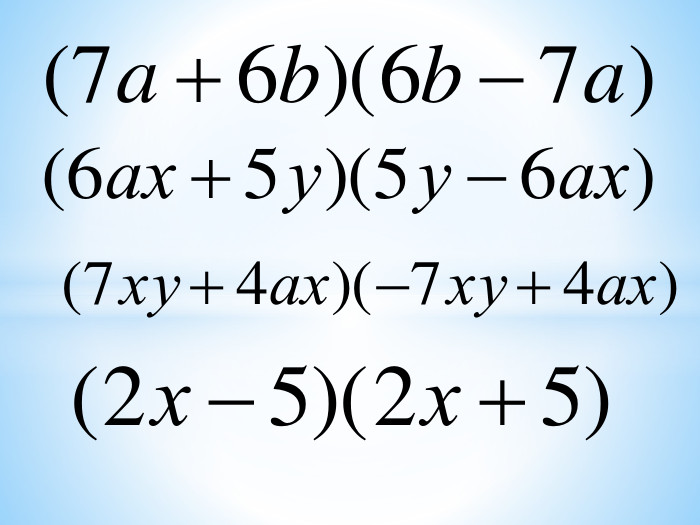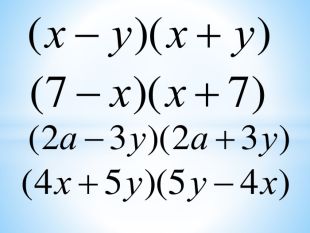"Формули скороченого множення." Презентація.
Про матеріал
«У математиці існує своя мова – формула».
Це урок-подорож до країни здоров'я. Учні використовують формули скороченого множення для перетворення виразів, де в них формується компетентне ставлення до власного здоров'я. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
До уроку
Різниця квадратів двох виразів Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку