Формування математичної грамотності через інтегровані навчальні  предмети математика та еврика

       Ми живемо в період інтенсивного розвитку інформаційно-комунікаційних технологій, які міцно увійшли в наше життя. Сучасна молода людина повинна вміти швидко й успішно адаптуватися до соціальних змін.

  Математична освіта сприяє розвитку інтелекту особистості, формує вміння науково мислити, здатність аналізувати, долати труднощі, а отже, виховує вольові якості та навчає отримувати радість від одержання нових знань. Метою освітньої галузі «Математика» є формування предметної математичної та ключових компетентностей, необхідних для самореалізації учнів у сьогоденні.

У класах, що працюють за програмою науково-педагогічного проекту освітня галузь «Математика» реалізується в курсі початкової школи через інтегровані навчальні предмети Математика та Еврика, Навчаємося разом.^[1]

     Особливістю уроків математики є пропедевтика математичних знань та розвитку мислення. Навчальні завдання розроблені за принципом наступності й перспективності змісту. Уроки побудовано з детально продуманими міжпредметними зв’язками. Математичні вміння та навички у дітей формуються не лише на уроках математики, а й під час вивчення інших предметів. Так, на кожному уроці «Навчаємося разом» на сторінці «Запам’ятайлика» дітям демонструють 4 приклади. Учні повинні не просто їх запам’ятати та відтворити, але і знайти закономірність, для легшого запам’ятовування. Ця вправа тренує у школярів пам’ять, вдосконалює обчислювальні вміння, розвиває логічне мислення. На «Ігровій сторінці» діти працюють над завданнями із сірниками, умова яких – додати чи забрати певну кількість сірників, щоб отримати рівність з метою розвитку логічного мислення.

   Але зауважимо, що разом із цим, дані завдання тільки доповнюють уміння та навички  учнів, а уроки не об’єднанні єдиною темою.

   Навчання за програмою науково-педагогічного проекту «Інтелект України» активізує пізнавальну активність учнів. На уроках системно застосовуємо значну кількість інтерактивних методів навчання, різноманітні завдання та інтерактивних вправи.  Всі види завдань супроводжуються  презентацією або відео поясненням, що підсилює інтерес до навчання.  Ніхто із учнів не скаже, що на уроках математики  не цікаво або нудьгував.

   Одним із перших завдань на уроках в 1 класі є :

Вправа  «Презентація чисел»

1. Учитель вмикає презентацію цифр. (ІКТ)

2. Після перегляду ставимо запитання, які направлені на формування у дітей математичних знань:

- Яке число було першим? Якою цифрою воно позначається?

- Яке число було другим? Якою цифрою воно позначається?

- Яке число було останнім? Якою цифрою воно позначається?

Наступні кілька запитань ставимо з метою тренування пам’яті, вироблення вміння концентрувати увагу як на об’єкті в цілому, так і на деталях об’єкта.

- Що було зображено на першому малюнку?

- Хто був зображений біля двійки?

- Як були розташовані човни на останньому малюнку?

- Що робив ведмедик?

 

Вправа «Числа на карнавалі»

    Дана вправа проводиться з метою удосконалення обчислювальних навичок,  бачити  співвідношення між компонентами арифметичних дій, розвиває мислення, пам'ять .

5  +  =  8

Проводимо дане завдання у вигляді гри, де числа, що «їдуть» на  маскарад, «одягають» маски. Діти намагаються відгадати, яке число «одягло» маску.

Обчислювальна культура є тим необхідним запасом знань та вмінь, без якого неможливо розв’язати жодної математичної задачі. Вміння швидко й точно виконувати обчислення є фундаментом вивчення математики. 

З метою формування обчислювальних умінь та навичок  систематично використовуємо усні вправи «Будиночок чисел», «Ракета», що сприяють засвоєнню матеріалу.  

З метою автоматизації обчислювальних навичок вивчаємо  алгоритми додавання, віднімання, множення та ділення одноцифрових та багатоцифрових чисел.

До кожної теми підібрані завдання для відпрацювання навичок обчислення.  Головне, що дітям пропонують виконати завдання, а не зобов’язують. 

На кожному уроці  діти виконують вправу «Фотоапарат», що передбачає розвиток зорової пам’яті, уваги, спостережливості. За цією вправою учні вчать і визначення, і вчать таблицю множення, одиниці вимірювання, склад чисел.

   На уроках учні працюють колективно,  але найкраще співпрацюють в парах. 

  ◊робота в парах

   Заповни порожні клітинки. Попрацюй у парі. Розкажи однокласникам приклади з пам’яті.

4 - 3 = □            3 + 1 = □          4 + 1 = □

5 - 4 = □  5 + 1 = □         4 - 1 = □

    Одними із завдань  математичної грамотності є розвиток концентрації уваги, вміння зосереджуватися на кількох об’єктах одночасно, формулювати припущення та встановлювати послідовність певних дій. Такої вправою є «Коректурні проби»

        Розв’язання задач сприяє засвоєнню учнями арифметичних дій, усвідомленню зв'язку між компонентами й результатами дій, залежності між величинами. Процес розв’язання задач є багатоетапним: він містить переклад словесного тексту на мову математики (побудова математичної моделі), математичні розрахунки і аналіз отриманих результатів. Важливе значення має ознайомлення учнів з різними методами рішення текстових задач: арифметичним, алгебраїчним, геометричним, логічним і практичним.   

     Розв’язання текстових задач сприяє  розвитку пізнавальних процесів та виховання вольових якостей; сприяє оволодінню прийомами розумової діяльності; удосконаленню вмінь будувати судження, робити висновки; формуванню у школярів мотивації їхньої навчальної діяльності, здатності й інтересу до цієї діяльності.

Вправи на формування умінь розв’язувати задачі

    Прочитай, прискорюючи темп. Відтвори з пам’яті. 

    Задачі із запитанням «Скільки залишилося?» називають задачами на знаходження остачі (різниці). Їх розв’язують за допомогою дії віднімання.

Умову до цих задач записуємо так:

Б. – 10 к.        Б. – було;

П. – 4 к.         П. – подарували;

З. - ? к.           З. – залишилося;     к. – кульки.                            
   ◊ Розглянь зразок розв’язання арифметичної задачі на знаходження остачі (різниці).

   На тарілці лежало 7 тістечок. Тарас узяв 3 тістечка. Скільки тістечок залишилося на тарілці?

 

 

 

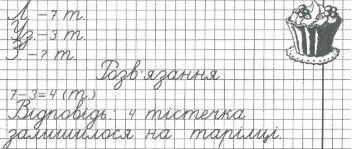
Відповідь записуємо згідно методичних рекомендацій  щодо оформлення письмових робіт з математики в початковій школі.

 Після закінчення навчання грамоти вводиться короткий запис відповіді задачі, наприклад: 5 кг цукру; 40 відер води.

Повну відповідь рекомендується записувати, починаючи з 3 класу. Якщо розв'язання задачі записано без пояснень, то відповідь бажано записувати повними реченнями. Повну відповідь слід будувати за загальними правилами побудови речень.

Якщо запис розв'язання задачі був із поясненням (повним чи коротким), то відповідь можна записувати коротко.

Зразки записів пояснень та відповідей:

7 + 3 = 10 (з. ) - у лінійку і клітинку .

Відповідь: 10 зошитів.

Відповідь: у мішку залишилося 50 кг цукру.

Відповідь: на 3 т більше.

Відповідь: посадили 20 дерев

   ◊  Допоможи Кнопочці дописати умову, розв’язання та відповідь до задачі на знаходження остачі (різниці).

   У Їжачка було 5 кактусів. Два кактуси він подарував Нюші. Скільки кактусів залишилось у Їжачка?

 

      ◊ Розв’яжи  алгебраїчну в робочому зошиті задачу на знаходження остачі (різниці).

    В учнів було d аркушів кольорового паперу. Для виготовлення новорічних іграшок вони використали 5 аркушів. Скільки аркушів кольорового паперу залишилося?

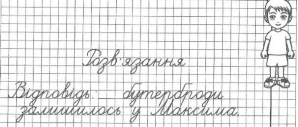     ◊ Допоможи Кнопочці розв’язати задачу, написавши умову, розв’язання й відповідь.

    У Максима було 10 бутербродів. Вісім

 бутербродів він з’їв. Скільки

бутербродів залишилося у Максима?

 

   Роботу над розв’язуванням задач з логічним навантаженням здійснюємо в системі.

  Послідовність роботи над задачами:

1. Читання умови задачі.

2. Учні називають варіанти відповідей.

3. Пояснення дітьми розв’язання задачі.

4. Виконання практичних дій. Моделювання рішення задачі.

5. Обирання правильної відповіді (тестове завдання).

6. Створення графічного малюнка.

 

    Задачі з логічним навантаженням знайомлять школярів з різними підходами вирішення математичних завдань.

    Навчальний матеріал предмета математика інтегрується з предметом еврика. На уроках еврики у дітей формується практичне вміння виконувати пошуково-дослідницькі завдання та розв’язувати задачі на винахідливість.   

   Маленькі школярі вчаться користуватися алгоритмом розв’язання таких задач:

1. Уважно прочитай, зрозумій та проаналізуй текст задачі.

2. Вияви та сформулюй суперечність між реальним станом об’єкта та бажаним.

3. Сформулюй ідеальний кінцевий результат, тобто визнач найкращий результат, якого прагнеш досягти. Витрати мають бути мінімальними.

4. Запропонуй кілька варіантів досягнення ідеального кінцевого результату.

5. Обери найкраще рішення.

    Розв’яжи винахідницьку задачу за цим алгоритмом. Заповни таблицю.

    У давнину іспанським селянам дошкуляли гризуни, які псували й нищили продукти в коморах. Але з часом іспанці все-таки знайшли вихід. Який саме – поміркуй.

1	Якщо.. То.. Але…	Іспанські селяни роблять запаси продуктів на майбутнє,
		вони почуваються впевнено,
		гризуни нищать запаси.
2	Якщо.. То… Але…	Селяни не робитимуть запасів,
		гризуни не шкодитимуть людям,
		людям без харчів важко вижити.
3	ОБ’ЄКТ МАЄ БУТИ Й… І…	Продукти мають зберігатися в коморах,
		продукти мають бути захищені від гризунів.
4	ІДЕАЛЬНИЙ КІНЦЕВИЙ РЕЗУЛЬТАТ	Комори встановлюють на високих міцних (дубових) гладких (тесаних) стовпах, і гризуни не можуть дістатися

    Робота за алгоритмом спонукає дітей до чіткого засвоєння умови задачі та з’ясування запитання до неї, вчить ретельно аналізувати ситуацію, розглядати різні шляхи вирішення завдання та виробляє вміння обирати найкращий варіант.

    Пропедевтика алгебри та геометрії не становить окремих розділів курсу математики початкових класів, предмети пов’язані з арифметичним матеріалом.

     Вивчення чисел – перший крок в ознайомленні з ідеєю математичної абстракції. Наступним кроком стає перехід від числа до буквеного числення.           

   У початкових класах учні знайомляться з виразом, що містить буквений компонент, вчаться знаходити числові значення таких виразів, застосовують буквені вирази для запису властивостей арифметичних дій. Алгебраїчна пропедевтика передбачає ознайомлення з поняттями «рівність», «нерівність», «змінна», «рівняння». Поняття буквеного виразу і рівняння застосовуються під час рішення задач. Розв'язуючи задачі, пов'язані з прямо і обернено пропорційними залежностями, молодші школярі знайомляться з одним із видів функціональної залежності.

Система вправ з алгебраїчної пропедевтики

   ◊ обчислення буквених виразів:

    Познач порядок дій та обчисли значення виразу 45 + 4 •b – 39,

якщо b = 5.

    ◊ рівняння:

   Числа залюбки «їздять» на карнавал. Яке число «сховалося» під маскою у, якщо у + 3 = 8? Обведи правильний варіант відповіді:

А) у = 5;         Б) у = 6;           В) у = 7.

   ◊ нерівності:

   Спираючись на переставний закон додавання й не виконуючи обчислень, порівняй вирази.      8 + b □ b + 8            d + 10 □ 9 + d

  ◊ задачі:

    Розв’яжи задачу. Обведи правильний варіант відповіді.

№1. На полиці стояло n книг. Діти взяли 5 книг. Скільки книг залишилося на полиці?

А) n; Б) n + 5; В) n – 5.

№2. У ведмедика було v банок меду. Узимку він з’їв мед із 8 банок. Скільки банок меду залишилося?

№3. Склади алгебраїчну задачу на знаходження остачі (різниці). Запропонуй однокласникам її розв’язати.

№4. Склади обернену задачу.

    У геометричній пропедевтиці головними об'єктами на площині є точка, пряма, відрізок, многокутник, коло і круг; у просторі (в порядку ознайомлення) — куб, призма, піраміда, циліндр, конус, куля. Учні засвоюють назви фігур та їхніх елементів, вчаться їх розпізнавати. Значна увага приділяється побудові і вимірюванню відрізків, побудові деяких плоских фігур, обчисленню периметра і площі прямокутників.

    Одним із завдань, що сприяють розвитку геометричної уяви, є завдання на визначення кількості геометричних фігур на малюнку.

    Послідовність роботи над вправою:

1. Діти самостійно визначають кількість геометричних фігур на малюнку.

 

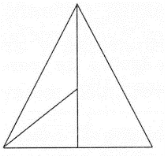
2. Називають варіанти відповідей.

3. Практичні дії. Накладають на малюнок геометричні фігури (від більшої до меншої).

4. Обирають правильну відповідь у тестовому завданні.

5. Перевіряють правильність виконання (за допомогою ІКТ).

 

Дидактична спрямованість вправи:

1. Розвиток конструктивного мислення.

2. Знання геометричних фігур.

3. Уміння сконцентрувати увагу на досліджуваному об’єкті.

Особлива увага приділяється розвитку просторових уявлень молодших школярів на уроках еврики.

В ігровій формі діти вчаться розв’язувати задачі за допомогою методу організованого перебору, методу графів, табличного методу та методу міркувань від супротивного, знайомляться з задачами на правило суми чи добутку. Учні засвоюють матеріал швидко та з цікавістю.

    До кожного уроку розроблено систему чіткого контролю за якістю засвоєння знань. Діти виконують на швидкість вправи на застосування отриманих на уроці знань, умінь та навичок.

Завдання «Великі перегони»

Ти – учасник великих перегонів. Обери машину, на якій будеш брати участь в авторалі. Обведи її.

Умови авторалі. Треба за 4 хвилини правильно розв’язати приклади. За кожний правильно розв’язаний приклад ти отримаєш 1 бал. Якщо в сумі набереш 24 бали, то одержиш Гран-прі. Розмалюй свій трофей!

    На основі методики вивчення математики, досвіду роботи вчителів, що працюють за Проектом вдосконалено математичну початкову освіту в проектних класах та підвищено ефективність уроків математики та  здобуття якісних знань сприяла чітка система дій:

1) Раціональний вибір мети і завдань уроку, його змісту і структури.

2)Застосування методів і прийомів активного навчання учнів з урахуванням вікових особливостей дітей молодшого шкільного віку.

3)Вдале поєднання колективних, групових та індивідуальних форм навчання, спрямоване на впровадження диференціації навчально-виховного процесу на основі досягнення обов’язкових результатів навчання.

 4) Систематичне використання різних видів роботи на уроці.

 5) Посилення зв’язку теоретичного матеріалу і практичних завдань.

 6)Удосконалення системи вправ, посилення їх прикладної спрямованості.

 7)Раціональне поєднання наочних посібників і технічних засобів навчання з новими інформаційними технологіями.

8) Удосконалення міжпредметних зв'язків.

9) Реалізація органічного зв'язку навчання, розвитку і виховання учнів.

10) Удосконалення форм і методів контролю успішності учнів.

 

 

^[1] Лагодюк В. Ю.,Федорчук І.В., Шляхи вдосконалення математичної початкової освіти у проектних класах «Інтелект України» http://www.divovo.in.ua/shlyahi-vdoskonalennya-matematichnoyi-pochatkovoyi-osviti-u-pr.html