Фрагмент уроку на тему "Властивості протилежних сторін і кутів паралелограма""

Тема. Властивості протилежних сторін і кутів паралелограма.

Постановка проблеми

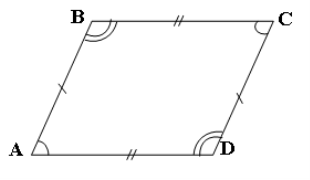      Побудувати паралелограм АВСD. Виміряти усі кути і сторони паралелограма. Порівняти ВАD і BCD та ABC і CDA (протилежні кути), а також сторони AD і BC

                       Рис.2.17                                та AB і CD (протилежні сторони).

      Протилежні сторони та протилежні кути паралелограма рівні (рис.2.17).

Формулювання проблеми

      Дослідити чи у всіх паралелограмах виконуються дані властивості.

Висунення гіпотез

      1) Побудувати декілька довільних паралелограмів, виміряти і порівняти їхні кути та сторони.

      2) Дослідити дані властивості, використовуючи раніше відомі твердження.

Перевірка гіпотез

      1) Недолік даної гіпотези полягає в тому, що різноманітних паралелограмів існує безліч, і ми не можемо всіх перевірити за допомогою вимірювання. Інший недолік – неточність вимірювання. Для збільшення точності вимірювання застосуємо GRАN-2D.

      Створимо дві довільних точки А та В. (Об’єкт → Створити з екрану → Точка). Проведемо через них пряму АВ  за допомогою функції Створення прямої через дві точки. За допомогою функції Створення паралельної прямої через довільну точку С будуємо пряму, паралельну до даної. Через точки А і С будуємо пряму АС і через точку В проводимо пряму, паралельну до неї. На перетині прямих b i c створимо точку D (рис.2.18).

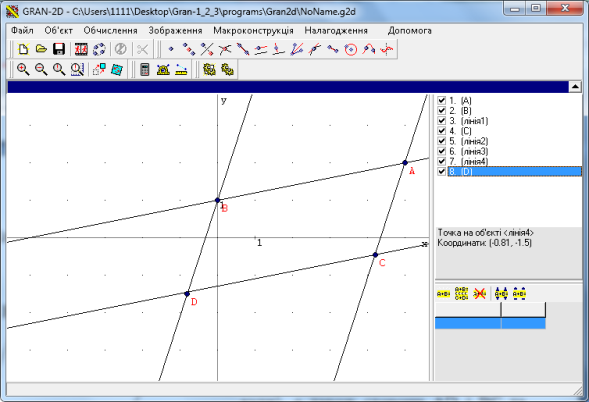
                                             Рис.2.18

      Будуємо ламану з вершинами A, B, C i D та приховаємо прямі AB, CD, BD i AC. ABCD – паралелограм, оскільки його протилежні сторони лежать на паралельних прямих. Виміряємо усі кути та сторони даного паралелограма. Бачимо що протилежні кути та протилежні сторони паралелограма рівні (рис.2.19).

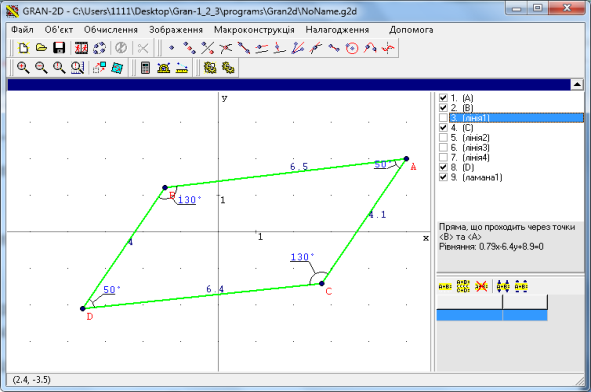
                                      Рис.2.19

      Перевіримо чи буде виконуватись дана властивість в інших паралелограмах. Аналогічно до того як будували паралелограм ABCD будуємо паралелограми EFHG i IJLK. Виміряємо усі сторони та кути цих паралелограмів. Оскільки паралелограм рухома конструкція, то рухаючи будь яку її вершину ми можемо одержати безліч паралелограмів. Бачимо, що досліджувана нами властивість виконується і в даних випадках (рис.2.20).

                                                 Рис.2.20

      2) Використовуючи відомі раніше теореми та властивості, ми можемо аналітично довести рівність протилежних кутів та сторін паралелограма для загального випадку.

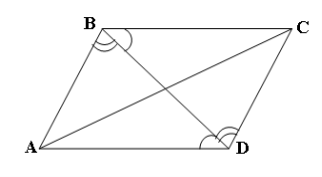      Будуємо паралелограм ABCD та проводимо його діагоналі AC і BD (рис.2.21).

      а) Розглянемо ∆ABD і ∆BCD. Паралелограм – це чотирикутник, у якого

                       Рис.2.21                                протилежні сторони паралельні, тобто лежать на паралельних прямих.

      Отже, ADIIBC і ABIICD. Тоді BDA  CBD, як внутрішні різносторонні при перетині січною BD паралельних прямих AB і CD, а ABD=BDC, як внутрішні різносторонні при перетині січною BD паралельних прямих AB і CD.

       BD – спільна для ∆ABD і ∆BCD, а отже дані трикутники рівні за другою ознакою рівності трикутників (сторона і два прилеглі до неї кути одного трикутника дорівнюють стороні і двом прилеглим до неї кутам другого трикутника).

      З рівності даних трикутників: ВАС =BCD; ABC=CDA (так як ABC =ABD+DBC, a CDA=CDB+BDA); AB=CD; AD=BC.

Аналіз результатів перевірки гіпотез

      Перевіримо одержані результати на практиці .

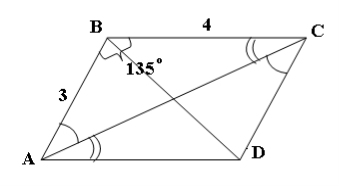
Дано: АВ=3см; ВС=4см;

АВС=135^о (рис.2.22).

Знайти усі сторони та кути паралелограма АВСD та    

                  Рис.2.22                                    порівняти протилежні.

Розв’язання

      Розглянемо ∆АВС і ∆СDА.

      АС – спільна. САD=ВСА, як внутрішні різносторонні при перетині січною АС паралельних прямих АD і ВС.

      АСD=ВАС, як внутрішні різносторонні при перетині січною АС паралельних прямих АВ і DС.

      Отже, ∆АВС =∆СDА. Звідси АDС=АВС=135^о; АВ =DС =3см;                      АD =ВС=4см.

ВАD=ВАС +САD; ВСD=DСА +АСВ.

Звідси ВАD=ВАС=1/2(360^о – 2*135^о)=45^о.

Висновки і узагальнення

      У паралелограма протилежні сторони рівні та протилежні кути рівні.

Повернення до проблемної ситуації

      Ми дослідили, що дійсно дані властивості виконуються для всіх паралелограмів.