Презентація "Трапеція та її властивості"
Про матеріал
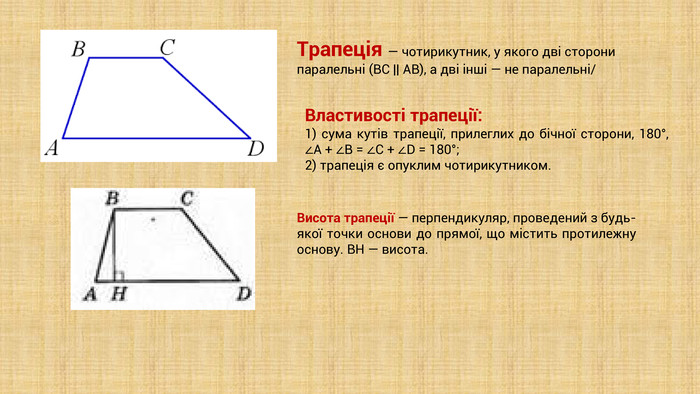
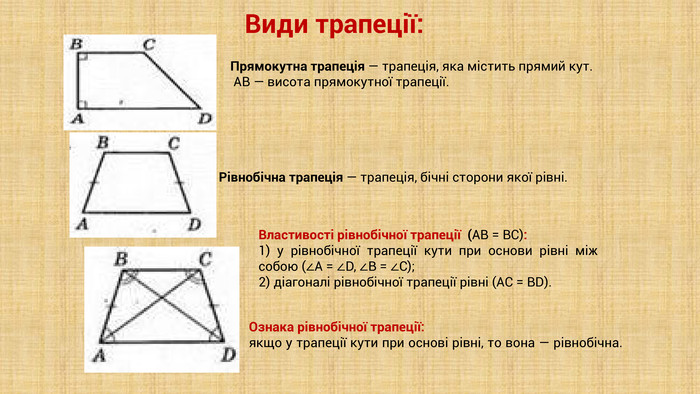
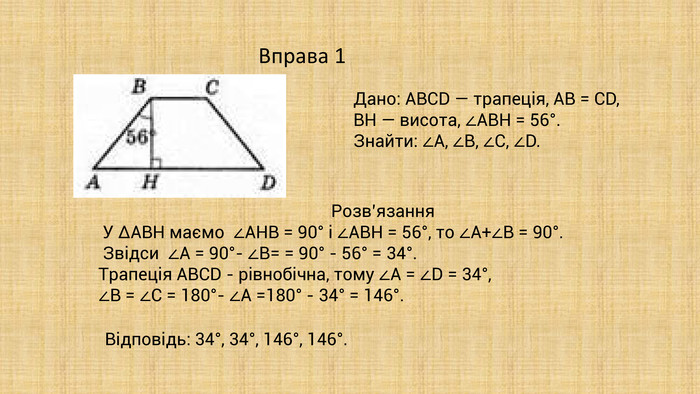
Презентація "Трапеція та її властивості" призначена для здобувачів освіти, які вивчають геометрію у 8 класі. В презентації дано означення трапеції,види трапеції, властивості і ознаки трапеції та наведено низку готових розв'язаних задач з трапецією. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


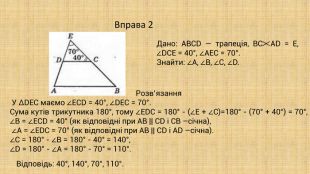
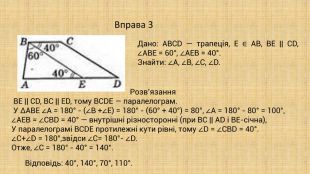
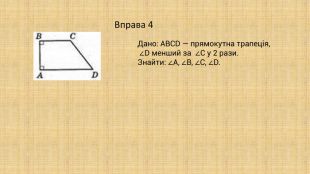
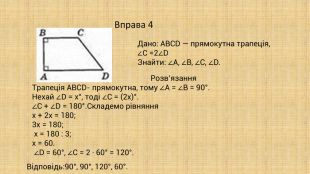


-

Кравченко Лілія
28.10.2024 в 21:15
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Перепелиця Тетяна Іванівна
14.04.2024 в 23:37
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Будрик Оксана
06.11.2023 в 01:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Дячкін Володимир
31.10.2023 в 10:47
Дякую за роботу!
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Марина Голод
28.10.2023 в 22:56
Дякую за класну роботу
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Овчар Олена Анатоліївна
12.10.2023 в 09:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
09.11.2022 в 11:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Приходько Наталія Михайлівна
08.11.2022 в 19:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кісель Тетяна Миколаївна
20.10.2022 в 20:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 6 відгуків