Функції. Побудова графіків функцій

Урок алгебри і початків аналізу, 10 клас

Тема уроку: Функції. Побудова графіків функцій

Мета уроку: Відновити  в пам'яті поняття функції, властивості  та види функцій, графіки функцій; розвивати  навички  побудови графіків функцій, застосовуючи перетворення графіків; збагатити досвід учнів в отриманні нових знань на основі вже наявних теоретичних знань, а також через використання знайомих ситуацій практичного характеру. Розвивати логічне мислення учнів через формування  вмінь будувати графіки функцій,  уміння аналізувати власні потреби, вибору відповідної позиції на кожен етап уроку. Виховувати графічну культуру учнів.

Форми роботи: групова, індивідуальна, фронтальна з використанням ІКТ

Очікувані результати: учні знають поняття функції, властивості функції,

вміють використовувати знання графіків основних функцій для побудови графіків більш складних функцій;мають навички роботи в групі.

Обладнання: презентація, папка з завданнями.

Девіз уроку: «Недостатньо знати, треба використовувати» І. Гете.

Хід уроку

І. Організаційний момент

ІІ. Мотивація навчальної діяльності учнів. Мета і завдання уроку

Поняття функції сягає своїм корінням в ту далеку епоху, коли люди вперше зрозуміли, що оточуючі їх явища взаємопов'язані. Вони ще не вміли рахувати, але вже знали, що, чим більше оленів вдасться вбити на полюванні, тим довше плем'я буде позбавлено від голоду, чим сильніше натягнута тятива у лука,  тим далі полетить стріла.

Пізніше, високого рівня досягла математика в Стародавньому Вавілоні.  Для полегшення обчислення вавилоняни склали таблиці зворотних чисел, таблиці квадратів і кубів чисел і навіть для суми квадратів чисел і їх кубів. Інакше кажучи це було табличне завдання функцій: у = х²; у = х³;  у = х² + х³.

Арабські ж вчені ввели нові тригонометричні таблиці і вдосконалили таблиці хорд, складені Птолемеєм. У дослідженнях аль-Біруні вперше зустрічаються думки  про всілякі залежності між величинами.

У середні століття почалося дослідження загальних залежностей функції, в яких були важливі досягнення Миколи Оресма, Рене Декарта, П'єра Ферма, Ісаака Ньютона, Готфріда Лейбніца і багатьох інших.

Слід зазначити, що в залежності від природи множин Х і У термін «функція» в різних розділах математики має ряд корисних синонімів: відображення, відповідність, перетворення і так далі.

Мета цього уроку – за допомогою наших дослідницьких груп більше дізнатися про функцію та перетворення графіків функцій.

ІІІ.  Історична сторінка

Дослідницька група істориків

(учнівські презентації  англійською мовою про І. Ньютона та на німецькою мовою про Г. Лейбніца, ознайомлення з перекладом математичних термінів на  іноземні мови)

ІV. Актуалізація отриманих знань і вмінь.

Не досить володіти премудрістю, потрібно також вміти користуватися нею

( робота в парах)

1. Які із ліній, зображених на рисунку, є графіком функції? Чому?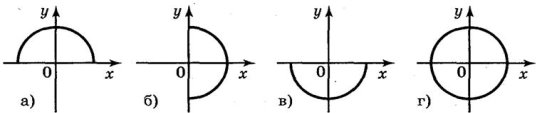

Відповідь: а); в).        

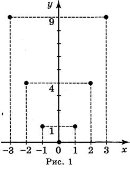
2. Функцію задано формулою у = x² на області визначення 

D = {-3; -2; -1; 0; 1; 2; 3}. Задайте її за до­помогою: а) таблиці; б) графіка.

Відповідь: а)

3. Знайдіть значення функції:   a) f(x) =  у точках 1; -1; 5;

б) f(x) =  у точках 3; 12; 52.

Відповідь: а) f(1) = 2, f(-1) = 0; f(5) = 1,2;  б) f(3) = 0;  f(12) = 3;  f(52) = 7

4. Знайдіть область визначення функції:

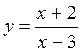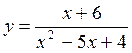а) у = х² + х³; б)  ; в)  ; г) .

Відповідь:

a) D(y) = R; б) D(y) = (-; 3)  (3; +); 

в) D(y) = (-;l)  (l;4)  (4;+);     г) D(y) = [-6;+).

5. Знайдіть область значень функції: а) у =; б) у =  -1.

Відповідь: а) Е(у) = [2; +); б) Е(у) = [1; +).

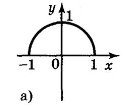
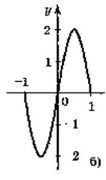
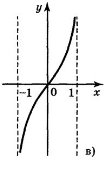
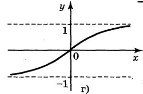
 6. Для функцій, графіки яких зображено на рис., вкажіть D(y) і Е(у).

Відповідь:

а) D(у) = [-1;1]; Е(у) = [0;1];б) D(y) = [-1;1]; E(y) = [-2;2];

в) D(y) = (-1;1); E(у) = R;    г) D(y) = R; Е(у) = (-1;1).

7. Користуючись графіками функцій, зображених на рисунку, вкажіть проміжки зростання і спадання функцій.

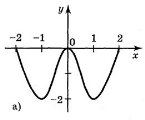
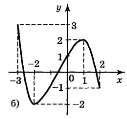
Відповідь: а) на кожному з проміжків [-1;0], [1;2] функція зростає, на кожному з проміжків [-2;-1], [0;1] функція спадає;

б) на кожному з проміжків [-3;-2], [1;2] функція спадає; на проміжку [-2;1] функція зростає;

8. Якіі з функцій, графіки яких зображено на рисунку, є пар­ними, а які непарними?

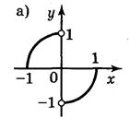
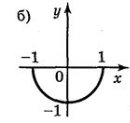
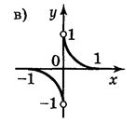
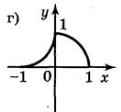
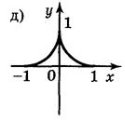
Відповідь: непарні — а), в); парні — б), д).

Музична пауза

Леонард Ейлер у своїй роботі "Дисертація про звук", написаної в 1727 році говорить: "Моєю кінцевою метою в цій праці було те, що я прагнув представити музику як частину математики і вивести в належному порядку з правильних підстав все , що може зробити приємним об'єднання і змішування звуків ".

Своє ставлення до математики і музики вчені висловлювалися в своїх особистих листування. Так, наприклад,  Лейбніц в листі Гольдбаху пише: "Музика є прихована арифметична вправа душі, що не вміє рахувати". На що Гольдбах йому відповідає: "Музика - це прояв прихованої математики".

( пісня англійською мовою)

V. Систематизація знань

Пригадаємо, як виглядають графіки деяких функцій і які перетворення з ними можуть відбуватися

Доповідь учня : Графіком функції називається сукупність всіх точок на площині, прямокутні координати яких х і у задовольняють рівняння y = f (x). Графічне зображення функції має важливе значення для її вивчення. На графіку функції часто безпосередньо видно такі її особливості, які можна було б встановити лише шляхом тривалих обчислень. Якщо між величинами х і у існує функціональний зв'язок, то байдуже, яку з цих величин вважати аргументом, а яку - функцією.

( Показ презентації)

VІ. Поглиблення знань, відпрацювання навичок

«Те, що я встиг пізнати – чудово. Сподіваюся, таке ж чудове те, що мені доведеться пізнати.»   Сократ

О, скільки нам відкриттів дивних

Готує наш просвіти дух!

Як треба графік будувати складний

Дізнаємось сьогодні ми!

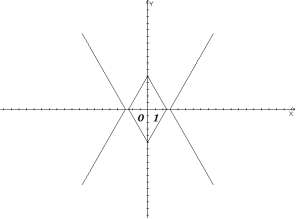Побудова графіків,  які  містять модулі

Побудуємо: | y | = | 2 | x | - 3 | -1 по кроках.

1) Y = | x |

2) Y = 2 | x | - розтяг вздовж осі у в 2 рази

3) Y = 2 | x | - 3 – паралельне перенесення на 3

одиниці вниз вздовж  осі у

4) Y = | 2 | x | - 3 | - симетричне відображення точок графіка, для яких 2 | x |-3<0  відносно  осі х

5) Y = | 2 | x | - 3 | -1 – паралельне перенесення вздовж осі у на 1 одиницю вниз

6) Y = || 2 | x | - 3 | -1 | - симетричне відображення точок графіка, для яких

|2|x| - 3 |- 1 > 0 відносно осі х.

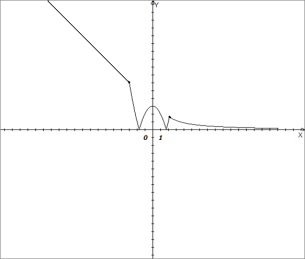Графік кусочно-заданих функцій

Побудуємо графік:

                      - х+3 , якщо    x ≤   -3

f(x)=               |x²-3| ,  якщо     -3 ≤ x ≤ 2,2

             ,     якщо    x ≥ 2,2

Беремо графіки не повністю, а лише їх частини на заданому проміжку, а потім з’єднуємо.
 

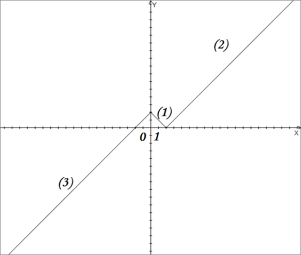
Метод  лінійного сплайну

Метод лінійного сплайну– це неперервна

кусково-лінійна функція. Її  графіком є

ламана з двома нескінченними кінцевими

ланками. Наприклад: y=x +| x - 2| - |x|

 х+2 , якщо    х < 0    (3)

у=  -х+2 ,  якщо  0 ≤ х ≤ 2    (1)

 х-2 ,  якщо   х >2     (2)

VІІ. Домашнє завдання:   тестові завдання або відтворити на графіку кусочно-заданих функцій формули, якими задаються ці функції.

Урок  закінчемо словами математика Олексія Миколайовича Крилова: „Рано чи пізно будь-яка правильна математична ідея знаходить застосування в тій чи іншій справі. Завтра математика стане ще могутнішою, ще важливішою і потрібнішою для людей, ніж сьогодні.”

VІІІ. Підсумки уроку

(презентація)

Графіки функцій – це не просто множина точок на координатній площині. 

Це – життя…

Творчість…

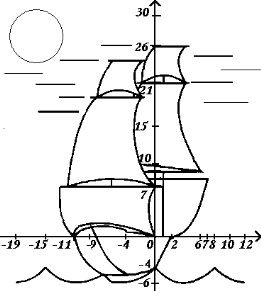І краса…