функціональні співвідношення для многочленів

ЗМІСТ
РОЗДІЛ І. Основні теоретичні відомості.
1.1 Поняття многочлена однієї змінної. Операції над многочленами.
1.2 Корені многочлена. Теорема Безу та теорема Вієта.
1.3 Кратні корені. Похідна многочлена.
1.4 Многочлени від декількох змінних
РОЗДІЛ ІІ. Основні типи завдань для підготовки з теми
Основні поняття про многочлени однієї змінної
2.2.1. Основні поняття про многочлени однієї змінної
2.3.1. Теорема Безу та наслідки з неї
2.3.3. Теорема про раціональний корінь многочлена
2.3.4. Теорема Вієта. Узагальнена теорема Вієта
Список використаної літератури
РОЗДІЛ І. Основні теоретичні відомості.
Означення. Многочлен – це функція спеціального вигляду: ![]() a₀zⁿ +a₁ zn-1+…+an ,
a₀zⁿ +a₁ zn-1+…+an ,![]() .
.
Змінну z і коефіцієнти вважатимемо комплексними. Найбільш поширені такі форми запису многочлена:
![]() a₀+a₁z+a₂z²+…+anzⁿ– за зростаючими степенями;
a₀+a₁z+a₂z²+…+anzⁿ– за зростаючими степенями;
![]() a₁zⁿ +a₂zn-1+…+an-1z+an – за спадними степенями.
a₁zⁿ +a₂zn-1+…+an-1z+an – за спадними степенями.
Означення. Степенем многочлена ![]() називають найвищий показник, із яким z входить до многочлена з коефіцієнтом, який не дорівнює 0.
називають найвищий показник, із яким z входить до многочлена з коефіцієнтом, який не дорівнює 0.
Над многочленами здійснюють дві основні алгебраїчні операції: додавання і множення. Застосуємо форму запису многочлена за зростаючими степенями.
Означення. Сумою многочленів ![]() a₀+a₁z+a₂z²+…+anzⁿ і
a₀+a₁z+a₂z²+…+anzⁿ і ![]() b₀+b₁z+b₂z²+…+bszs називають многочлен
b₀+b₁z+b₂z²+…+bszs називають многочлен ![]() +
+![]() із коефіцієнтами сі такими, що сі=aі+bі..
із коефіцієнтами сі такими, що сі=aі+bі..
Означення. Добутком ![]() і
і ![]() називають многочлен
називають многочлен ![]() , коефіцієнти якого обчислюють за таким правилом:
, коефіцієнти якого обчислюють за таким правилом: ![]()
Із цього правила випливає правило множення многочленів як двох сум.
Означення (формально-алгебраічне). Два многочлена називають рівними, якщо вони мають однакові коефіцієнти при однакових степенях z.
Означення (теоретико-функціональне). Дві функції (у тому числі й многочлен) називають рівними, якщо: 1) у них однакові області визначення; 2) за однакових значень аргументу вони набувають однакових значень.
Властивості операцій:
1)![]() +
+![]() =
=![]() +
+![]() – комутативність додавання;
– комутативність додавання;
2) ( ![]() +
+![]() + h
+ h![]() =
=![]() +
+![]() + h
+ h![]() ) – асоціативність додавання;
) – асоціативність додавання;
3) ![]() =
=![]() – комутативність множення;
– комутативність множення;
4) ![]() h
h![]() h
h![]() –асоціативність множення;
–асоціативність множення;
5) ![]() h
h![]() =
= ![]() h
h![]() +
+ ![]() h
h![]() – дистрибутивність.
– дистрибутивність.
Ділення многочленів з остачею. Найбільш спільний дільник (НСД)
Означення. Поділити многочлен ![]() на
на ![]() з остачею – це означає знайти пару таких многочленів
з остачею – це означає знайти пару таких многочленів ![]() і
і ![]() щоб
щоб ![]() +
+![]() , причому
, причому ![]()
![]() або степінь
або степінь ![]()
Теорема. Для будь-яких многочленів ![]() й
й ![]() , де
, де ![]() , де можливо ділення з остачею, причому
, де можливо ділення з остачею, причому ![]() і
і ![]() визначаються однозначно.
визначаються однозначно.
Многочлен ![]() називають остачею від ділення многочлена
називають остачею від ділення многочлена ![]() на
на ![]() ,
, ![]() – часткою.
– часткою.
Означення. Говоритимемо, що многочлен ![]() ділиться на многочлен
ділиться на многочлен ![]() без остачі, якщо
без остачі, якщо ![]() (ділення без остачі позначатимемо так:
(ділення без остачі позначатимемо так: ![]() .
.
Означення. Спільним дільником многочленів ![]() і
і ![]() називають такий многочлен
називають такий многочлен ![]() , на який і
, на який і ![]() , і
, і ![]() діляться без остачі.
діляться без остачі.
Означення. Найбільшим спільним дільником многочленів ![]() і
і ![]() називають такий їх спільний дільник, який ділиться на будь-який їх спільний дільник.
називають такий їх спільний дільник, який ділиться на будь-який їх спільний дільник.
Для подальшого знаходження найбільшого спільного дільника сформулюємо властивості подільності.
1) Якщо ![]() , а
, а ![]() , то
, то![]() .
.
Доведення.
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() Отже
Отже ![]() .
.
2 )Якщо ![]()
![]() .
.
3) Якщо![]() і
і ![]() .
.
4) Будь-який многочлен ділиться на многочлен нульового степеня.
Доведення.
Нехай f(z)=![]()
![]() .
. ![]() у вигляді
у вигляді
![]() =
=![]() . Отже
. Отже ![]()
5) Якщо ![]() .
.
6) ![]() то вони відрізняються постійним множником.
то вони відрізняються постійним множником.
Доведення.
Оскільки ![]()
Тоді ![]()
![]()
![]() [12]
[12]
Означення. Многочлени ![]() називають взаємно простими, якщо їх спільним дільником є многочлен нульового степеня (число не рівне нулю).
називають взаємно простими, якщо їх спільним дільником є многочлен нульового степеня (число не рівне нулю).
1.2 Корені многочлена. Теорема Безу та теорема Вієта.
Нехай задано многочлен ![]() .
.
Означення. Число ![]() називають коренем многочлена f(z), якщо
називають коренем многочлена f(z), якщо
f(![]() )=
)=![]() .
.
Теорема Безу. Остача від ділення многочлена ![]() на многочлен спеціального вигляду
на многочлен спеціального вигляду ![]() дорівнює значенню многочлена при
дорівнює значенню многочлена при ![]() , тобто
, тобто ![]() . [11]
. [11]
Доведення. Застосуємо теорему про ділення многочлена з остачею до многочленів ![]() та
та ![]() Тоді існують такі
Тоді існують такі ![]() , що
, що
![]() , (r(z)=r),
, (r(z)=r),
причому або ![]() або степінь
або степінь ![]() менша за степінь многочлена
менша за степінь многочлена ![]() .
.
Розглянемо при ![]() при z=с:
при z=с:
![]() .
.
Наслідок. Для того щоб число ![]() було коренем многочлена f(z), необхідно й достатньо, щоб f(z) ділився на
було коренем многочлена f(z), необхідно й достатньо, щоб f(z) ділився на ![]() без остачі.
без остачі.
Доведення. Необхідність.
Нехай ![]() корінь многочлена f(z), тобто f(
корінь многочлена f(z), тобто f(![]() )=0. Застосуємо до f(z) і g(z)=z–c теорему про ділення з остачею. За теоремою Безу r=f(α)=0. Отже, f(z) ділиться на (z–с) без остачі.
)=0. Застосуємо до f(z) і g(z)=z–c теорему про ділення з остачею. За теоремою Безу r=f(α)=0. Отже, f(z) ділиться на (z–с) без остачі.
Основна теорема алгебри. Будь-який многочлен степеня ![]() має принаймні один, комплексний корінь.
має принаймні один, комплексний корінь.
Традиційне доведення цієї теореми використовувало наступні леми, які мають самостійний інтерес.
Наведемо їх без доведення.
Лема 1. (Лема про вищий член многочлена).
Нехай задано ![]() степеня
степеня ![]() і задано число
і задано число ![]() , тоді таке існує число
, тоді таке існує число ![]() , що як тільки
, що як тільки![]() , то
, то
![]() .
.
Лема2. (Лема про зростання модуля многочлена).
Нехай задано многочлен f(z)= a0zn+ a1 zn-1+ a2 zn-2+...+an степеня n![]() 1 і задано число М>0. Тоді існує число P>0 таке, що як тільки
1 і задано число М>0. Тоді існує число P>0 таке, що як тільки ![]() , то
, то![]() .
.
Лема 3. (Лема Д’Аламбера).
Нехай задано многочлен f(z)= a0zn+ a1 zn-1+ a2 zn-2+...+an степеня n![]() 1 і задано число z0, що не є коренем многочлена f(z). Тоді існує таке число h, що
1 і задано число z0, що не є коренем многочлена f(z). Тоді існує таке число h, що ![]() .
.
Розглянемо наслідки основної теореми алгебри.
Наслідок 1. Многочлен ![]() -го степеня має
-го степеня має ![]() коренів, де кожен корінь враховують таку кількість разів, яка дорівнює цього кратності.
коренів, де кожен корінь враховують таку кількість разів, яка дорівнює цього кратності.
Наслідок 2. Будь-який многочлен можна розкласти на лінійні множники в області комплексних чисел.
![]() ,
, ![]()
Наслідок 3. Нехай задано два многочлени ![]() степенів
степенів ![]() , значення яких збігається в
, значення яких збігається в ![]() точці, тобто
точці, тобто
![]()
![]()
.....................................................
![]()
Тоді многочлени ![]() є рівні (у формально-алгебраїчному сенсі).
є рівні (у формально-алгебраїчному сенсі).
Наприклад, рівняння ![]() може мати раціональними коренями числа виду
може мати раціональними коренями числа виду ![]() , де
, де
![]()
![]()
Проте, на практиці частіше користуються не самою теоремою, а її наслідком 2.
Кожне рівняння ![]() з цілими коефіцієнтами легко привести до
з цілими коефіцієнтами легко привести до ![]() . Для цього потрібно обидві частини рівняння
. Для цього потрібно обидві частини рівняння
![]() помножити на
помножити на ![]() та зробити заміну:
та зробити заміну: ![]() , тоді отримаємо
, тоді отримаємо ![]()
Тобто, в рівнянні ![]()
![]()
![]()
Теорема 2. (необхідна умова існування дійсного кореня) Для того, щоб число ![]() (НСК
(НСК ![]() було коренем рівняння
було коренем рівняння ![]()
![]() необхідно щоб при довільному цілому
необхідно щоб при довільному цілому ![]() число
число ![]() .
.
На практиці в якості числа ![]() обирають
обирають ![]() .[10]
.[10]
1.3 Кратні корені. Похідна многочлена.
Означення. Число α називають k-кратним коренем многочлена ![]() якщо
якщо ![]() ділиться на
ділиться на ![]() і не ділиться на
і не ділиться на ![]() .
.
Щоб отримати умову існування k-кратного кореня, треба знати поняття похідної від многочлена.
Многочлен, являє собою комплексну функцією комплексної змінної, оскільки змінна z і коефіцієнти при степенях z – комплексні числа. Хоча формально поняття границі для комплексної функції комплексної змінної не відрізняється від поняття границі для дійсної функції, фактично воно стає більш жорстким. Це пов’язано з тим, що околом точки для дійсної змінної є інтервал, а околом у комплексній області є відкритий круг. Тому ми не можемо використати знання з математичного аналізу за перший курс. Через це ми незалежно від математичного аналізу введемо поняття похідної многочлена (як з’ясується на старших курсах воно узгоджується з відповідними поняттями функції комплексної змінної).
Означення. Похідною многочлена ![]() називають многочлен
називають многочлен
![]() .
.
Виходячи з означення похідної для многочлена можна довести такі правила знаходження похідної:
1,2![]()
3![]()
Теорема. Нехай α – k-кратний корінь многочлена ![]() . Тоді α є корінь кратності k-1 для його похідної
. Тоді α є корінь кратності k-1 для його похідної ![]() .
.
Доведення. Припустимо, що α – k-кратний корінь, тоді
![]() .
.
Потрібно довести, що
![]() .
.
Виходячи з правил обчислення похідних маємо
![]()
Це означає, ![]() .
.
Залишилося довести, що ![]() .
.
Позначимо ![]()
Припустимо супротивне: що ![]()
Тоді ![]()
За припущенням ![]() , а тоді і
, а тоді і ![]() , а це суперечить тому, що
, а це суперечить тому, що
![]() . Маємо суперечність. Теорему доведено.
. Маємо суперечність. Теорему доведено.
Часто в математиці потрібно розглядати многочлени, які залежать не від однієї, а від двох, трьох, взагалі кажучи, від декількох змінних.
Нехай![]() – n змінних
– n змінних ![]() (або
(або ![]() невідомих),
невідомих), ![]() – числа.
– числа.
Означення 1. Вираз ![]() , де
, де ![]() ,
,![]() –елемент поля
–елемент поля ![]() , називають одночленом від змінних
, називають одночленом від змінних![]() .
.
Суму ![]() називають степенем одночлена.
називають степенем одночлена.
Означення 2. Два одночлена називаються рівними, якщо:
![]()
Два одночлена називаються подібними, якщо:
![]()
Означення 3. Многочлен від багатьох змінних ![]() над полем
над полем ![]() (тобто є коефіцієнтом з поля Р) називається сума скінченої кількості одночленів.
(тобто є коефіцієнтом з поля Р) називається сума скінченої кількості одночленів.
Наприклад:![]()
Означення 4. Степенем многочлена ![]() (за сукупністю змінних) називається найбільший із степенів його одночленів (членів).
(за сукупністю змінних) називається найбільший із степенів його одночленів (членів).
Означення 5. Степенем многочлена ![]() відносно змінної
відносно змінної ![]() називається показник, з яким
називається показник, з яким ![]() входить в члени цього многочлена.
входить в члени цього многочлена.
Означення 6. Два многочленна від змінних ![]() з коефіцієнтами з одного і того ж поля Р називається рівними, якщо вони складаються з одних і тих же членів (може відрізнятися тільки порядком запису членів).
з коефіцієнтами з одного і того ж поля Р називається рівними, якщо вони складаються з одних і тих же членів (може відрізнятися тільки порядком запису членів).
Серед многочленів від декількох змінних виділяють декілька з них, які не змінюються при жодній перестановці змінних. У такі многочлени всі змінні входять симетричним чином. Такі многочлени відіграють важливу роль у алгебрі.
Означення 7. Многочлен ![]() від n змінних над полем Р називають симетричним, якщо він не змінюється при будь-якій перестановці змінних.
від n змінних над полем Р називають симетричним, якщо він не змінюється при будь-якій перестановці змінних.
а) всі многочлени нульового степеня є симетричними многочленами;
б) сума, різниця і добуток симетричних многочленів від n змінних є симетричним многочленом від цих змінних;
в) якщо ![]() – симетричний многочлен від
– симетричний многочлен від ![]() , то
, то ![]() ) – симетричний многочлен.
) – симетричний многочлен.
г) симетричні многочлени від змінних ![]() над
над ![]() утворює підкільце в кільці
утворює підкільце в кільці ![]()
![]() всіх многочленів, яке називають кільцем симетричних многочленів над полем Р.
всіх многочленів, яке називають кільцем симетричних многочленів над полем Р.
Наступні n симетричних многочленів від n змінних називаються елементарними симетричними многочленами:
![]() ,
,
![]() ,
,
![]() ,
,
……………………………………………………………..,
![]() ,
,
![]() .
.
При n=2: ![]() ;
;
![]()
n=3: ![]()
![]()
![]()
Теорема (основна теорема про симетричні многочлени): ожен симетричний многочлен від змінних ![]() над полем Р є многочленом від елементарних симетричних многочленів
над полем Р є многочленом від елементарних симетричних многочленів ![]() з коефіцієнтами із поля Р.
з коефіцієнтами із поля Р.
Наслідок. Нехай ![]() – многочлен від однієї змінної над полем
– многочлен від однієї змінної над полем ![]() , (старший коефіцієнт = 1).
, (старший коефіцієнт = 1).
Тоді кожен симетричний многочлен (з коефіцієнтами із Р) від коренів многочленна ![]() буде многочленом від коефіцієнтів многочлена
буде многочленом від коефіцієнтів многочлена ![]() .
.
Теорема 3. (теорема єдиності) Кожен симетричний многочлен має єдине вираження у вигляді многочленів від елементарних симетричних многочленів. [14]
РОЗДІЛ ІІ. Основні типи завдань для підготовки з теми
Основні поняття про многочлени однієї змінної
Теорія многочленів у курсі математики середньої школи вивчається протягом багатьох років. Умовно процес вивчення цієї теми можна розбити на декілька етапів. [40]
Перший етап включає формування понять «числовий вираз» (починаючи з 3 класу), «буквений вираз» (з 4 класу) і закінчується темою «Одночлен» (у 7 класі).
На цьому етапі навчання основна увага приділяється формуванню умінь і навичок конструювання алгебраїчних виразів і знаходженню їх функціональних значень, тотожному перетворенню алгебраїчних виразів над конкретною числовою множиною.
У 6 класі в темі «Переставний і сполучний закони множення» зазначається, що названі закони дають змогу спрощувати вирази, що складаються з числових і буквених множників. Якщо вираз є добутком числа і однієї або кількох букв, то число називають числовим коефіцієнтом або просто коефіцієнтом. Коефіцієнти таких виразів, як а або ![]() , вважають такими, що дорівнюють 1, оскільки
, вважають такими, що дорівнюють 1, оскільки ![]() . Множення -1 на будь-яке число а дає число
. Множення -1 на будь-яке число а дає число ![]() . Тому числовим коефіцієнтом цього виразу є число -1. [2]
. Тому числовим коефіцієнтом цього виразу є число -1. [2]
Введення в 6 класі дії піднесення до натурального степеня дає можливість розширити «фронт» спрощення буквенних виразів, основу якого тепер складають означення степеня з натуральним показником, сполучний, переставний і розподільний закони додавання і множення. [3]
Приклад: Спростити вираз:
![]() .
.
Застосуймо розподільний закон:
![]() ;
;
Переставний закон множення:
![]() ;
;
Сполучний закон множення (спрощуючи вирази, що містять однакові множники) ![]() ;
;
Переставний і сполучний закон додавання:
![]() ;
;
Розподільний закон:
![]() . [21]
. [21]
Пояснення процедури перетворення виразів значно спрощується після введення поняття «подібні доданки»: подібні доданки можуть відрізнятися один від одного тільки коефіцієнтами (6 клас).
У курсі алгебри (7 клас) ще раз звертаються до поняття степеня з натуральним показником і доводять властивості степенів. Зазначені теоретичні відомості дають змогу ввести поняття «одночлен» на конструктивному рівні: вирази ![]() є добутками чисел, змінних і їхніх степенів. Такі вирази, а також числа, змінні та їхні степені називають одночленами.
є добутками чисел, змінних і їхніх степенів. Такі вирази, а також числа, змінні та їхні степені називають одночленами.
У 7 класі вводять означення многочлена: многочленом називається сума одночленів. Одночлени, з яких складається многочлен, називають членами многочлена. Степенем многочлена називають найбільший із степенів одночленів, що входять до його складу.
Введенням поняття «многочлен» починається другий етап вивчення елементів алгебри многочленів. Вводяться, за певними законами (правилами), дії додавання, віднімання, множення многочленів. При цьому наголошується замкненість множини многочленів стосовно цих дій: суму (різницю) і добуток будь-яких двох або декількох многочленів можна зобразити у вигляді многочлена. Зображення многочлена у вигляді добутку двох або декількох многочленів (серед яких можуть бути й одночлени) називають розкладом многочлена на множники. Способи розкладу: винесення спільного множника за дужки, спосіб групування, за формулами скороченого множення. [22]
Програмою з математики для шкіл та класів математичною профілю передбачено вивчення питань теорії подільності многочленів (ділення з остачею, теорема Безу, схема Горнера та ін.). Це допомагає при вивченні теорії многочленів використовувати аналогію з множиною цілих чисел, яка заснована на структурній однотипності множини многочленів та множини цілих чисел. Запропонована методична система вивчення теорії многочленів передбачає використання цієї аналогії.
Зокрема, підготовка до вивчення елементів теорії подільності многочленів (10 кл.) містить узагальнення відповідних знань та вмінь учнів за курс неповної середньої школи. При цьому увага зосереджується на означенні поняття многочлена, степеня многочлена, кореня многочлена, поняття многочлена нульового степеня, нульового многочлена; виконанні операцій над многочленами; елементах теорії подільності цілих чисел. [4]
Відзначимо, що теорія подільності може бути змістовно розвинута для досить великої кількості кілець, до яких належать кільця многочленів та цілих чисел. Тому природним та ефективним є використання аналогії, яка існує між цими теоріями.
Тому вивчення теоретичного матеріалу цієї теми можна розпочати з дослідження структури множини многочленів з раціональними коефіцієнтами відносно операцій додавання і множення, результати виконання яких потрібно подати у загальному вигляді:
![]() ,
, ![]()
![]()
![]() . [5]
. [5]
2.2 Система вправ і задач з теми «Многочлени однієї змінної: степінь многочлена, операції над многочленами» в шкільному курсі математики.
2.2.1. Основні поняття про многочлени однієї змінної
Тема «Многочлени від однієї змінної» являється першою темою у розділі «Алгебраїчні рівняння та нерівності вищих степенів», метою вивчення якого є – навчитися розв’язувати рівняння та нерівності вищих степенів різних видів. Оскільки рівняння з однією змінною розглядають як рівність виду ![]() , де
, де ![]() - функція або многочлен, тому виникає потреба у вивченні теорії многочленів.
- функція або многочлен, тому виникає потреба у вивченні теорії многочленів.
Оглянемо основні факти з теорії многочленів від однієї змінної: поняття, степінь многочлена, коефіцієнти; дії над многочленами, звітні та незвітні многочлени, їх вплив на деякі основні методи їх розв’язання задач з даної тематики. Практика показує, що задачі з теорії многочленів від однієї змінної широко представлені у текстах зовнішнього незалежного тестування та у різних математичних змаганнях, причому в різних видах формулювань та застосувань.
Означення. Многочленом степеня ![]() від змінної
від змінної ![]() будемо називати вираз виду
будемо називати вираз виду ![]() де
де ![]() – будь-які дійсні числа.
– будь-які дійсні числа.
Многочлен нульового степеня є многочленом – константою, тобто ![]() . Будемо також вважати многочленом константу, що рівна нулю, такий многочлен будемо називати нуль-многочленом (нуль-многочлен не має степеня, на відміну від інших многочленів).
. Будемо також вважати многочленом константу, що рівна нулю, такий многочлен будемо називати нуль-многочленом (нуль-многочлен не має степеня, на відміну від інших многочленів).
Терміни і позначення:
-
Многочлени від змінної
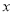 будемо позначати символами
будемо позначати символами 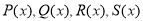 і т. д.
і т. д.
-
Степінь многочлена
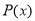 позначимо так:
позначимо так: 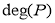 .
.
-
Числа
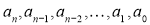 будемо називати коефіцієнтами многочлена
будемо називати коефіцієнтами многочлена 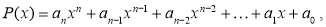
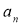 – старшим коефіцієнтом,
– старшим коефіцієнтом, 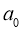 – вільним членом.
– вільним членом.
-
Нехай
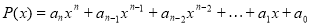 – даний многочлен і
– даний многочлен і 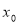 – деяке число, тоді
– деяке число, тоді 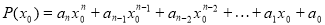 називається значенням многочлена
називається значенням многочлена 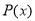 при
при 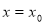 .
.
Означення. Число ![]() називається коренем многочлена
називається коренем многочлена ![]() , якщо при
, якщо при ![]() значення
значення ![]() .
.
- Доведіть, що:
- сума усіх коефіцієнтів многочлена ![]() обчислюється за формулою
обчислюється за формулою 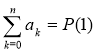 .
.
- сума коефіцієнтів многочлена ![]() , що стоять при парних (непарних) степенях х обчислюється за формулою:
, що стоять при парних (непарних) степенях х обчислюється за формулою: ![]()
![]() ;
;
- якщо многочлен ![]() з цілими коефіцієнтами і
з цілими коефіцієнтами і ![]() , то
, то ![]() .
.
Завдання№1.
1) Вказати степінь, старший і вільний коефіцієнти многочлена:
а)![]()
![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2) Знайдіть суми всіх коефіцієнтів наступних многочленів:
а)![]() , б)
, б)![]() , в)
, в)![]()
3) Дано многочлен ![]() . Знайти:
. Знайти: ![]() ; старший коефіцієнт і вільний член; суму всіх коефіцієнтів у канонічному розкладі многочленна; суму коефіцієнтів при парних; непарних степенях x:
; старший коефіцієнт і вільний член; суму всіх коефіцієнтів у канонічному розкладі многочленна; суму коефіцієнтів при парних; непарних степенях x:
а) ![]() ; б)
; б) ![]() ;
;
в)![]() ; д)
; д) ![]() .
.
4) Нехай многочлен ![]() такий, що для всіх
такий, що для всіх ![]()
![]() . Чи може
. Чи може ![]() містити непарні степені
містити непарні степені ![]() ?
?
5) Чи існує многочлен Р(х) з цілими коефіцієнтами такий, що Р(1) =11, Р(-1) = 0?
Вказівка. Використайте одну з властивостей 1) – 5).
Завдання№2. При яких обмеженнях на цілі числа ![]()
1) многочлен ![]() приймає при всіх
приймає при всіх ![]() парні (непарні) значення?
парні (непарні) значення?
2) многочлен ![]() приймає при всіх
приймає при всіх ![]() значення, що діляться на 3?
значення, що діляться на 3?
Розв’язання. 1) Значення ![]() при всіх
при всіх ![]() мають однакову парне тоді і тільки тоді, коли кожне із чисел
мають однакову парне тоді і тільки тоді, коли кожне із чисел ![]() ділиться на 2, тобто
ділиться на 2, тобто ![]() – непарне. При цьому парність всіх
– непарне. При цьому парність всіх ![]() однозначно визначається по парності числа
однозначно визначається по парності числа ![]() , таким чином, всі значення
, таким чином, всі значення ![]() парні (непарні) при парному
парні (непарні) при парному ![]() і парному (відповідно непарному)
і парному (відповідно непарному) ![]() .
.
2) Оскільки ![]() , то значення
, то значення ![]() при всіх
при всіх ![]() діляться на 3 тоді і тільки тоді, коли число
діляться на 3 тоді і тільки тоді, коли число ![]() ділиться на 3. При цьому кожне зі значень
ділиться на 3. При цьому кожне зі значень ![]() ділиться на 3 в тому і тільки в тому випадку, коли число
ділиться на 3 в тому і тільки в тому випадку, коли число ![]() ділиться на 3. Таким чином, всі значення
ділиться на 3. Таким чином, всі значення ![]() діляться на 3 за умови
діляться на 3 за умови ![]()
2.2.2. Дії над многочленами
Теорема1. Два многочлени P(x)=anxn+an-1xn-1+an-2xn-2+…+a1x+a0 та
Q(x)=bnxn+bn-1xn-1+bn-2xn-2+…+b1x+a0 рівні тоді і тільки тоді, коли n=m і аі=bi ![]() i=
i=![]() .
.
Тобто якщо ![]() і
і ![]() рівні многочлени, то для довільного числа
рівні многочлени, то для довільного числа ![]() їхні значення при
їхні значення при ![]() співпадають. Мають місце наступні теореми:
співпадають. Мають місце наступні теореми:
Теорема 2. Якщо ![]() , то
, то ![]() справедлива рівність
справедлива рівність ![]() .
.
Теорема 3. Якщо ![]() справедлива рівність
справедлива рівність ![]() , то
, то ![]() .
.
Теорема 4. Якщо ![]() , то існує таке число
, то існує таке число ![]() , що
, що ![]() .
.
Теорема 5. Якщо існує таке число ![]() , що
, що ![]() , то
, то ![]() .
.
Теорема 6. Нехай Р(х) і Q(x) – довільні многочлени, тоді:
-
функція
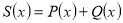 – теж многочлен, причому deg(S)
– теж многочлен, причому deg(S)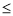 max(deg(P);deg(Q));
max(deg(P);deg(Q));
-
функція D(x)=P(x)Q(x) – теж многочлен, причому deg(D)=deg(P)+deg(Q), якщо Р(х)
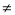 0 i Q(x)
0 i Q(x)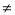 0.
0.
Завдання№3.
1) Скласти многочлен за даними його коефіцієнтами:
а) -![]() , 0,
, 0, ![]() , 0, 0, 0; б) 1, 0, 0, 0, 1, 0,
, 0, 0, 0; б) 1, 0, 0, 0, 1, 0, ![]() .
.
2) Визначити, які серед даних многочленів рівні: ![]() ;
;![]() ;
; 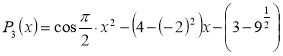 ;
; ![]() .
.
3) Знайти числа a , b і c, при яких справедлива тотожність:
а) ![]() ;
;
б) ![]() ;
;
г) ![]() ;
;
д) ![]() ;
;
е) ![]() .
.
4) Побудуйте многочлен з раціональними коефіцієнтами, мінімальне значення якого дорівнює: а) ![]() ; б)
; б) ![]() ; в) доведіть, що не існує многочлена
; в) доведіть, що не існує многочлена ![]() -ого степеня, що задовольняє умову пункту б); г) чи існують многочлени з цілими коефіцієнтами, один з яких задовольняє умову пункту а), а інший – умову пункту б)?
-ого степеня, що задовольняє умову пункту б); г) чи існують многочлени з цілими коефіцієнтами, один з яких задовольняє умову пункту а), а інший – умову пункту б)?
5) Складіть многочлен найменшого степеня з цілими коефіцієнтами, один з коренів якого: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
6) Знайдіть многочлен з цілими коефіцієнтами:
а) ![]() -ого степеня, серед коренів якого є число
-ого степеня, серед коренів якого є число ![]() ;
;
б) ![]() -ого степеня серед коренів якого є число
-ого степеня серед коренів якого є число ![]() ;
;
в) доведіть існування многочлена з цілими коефіцієнтами ![]() -ого степеня, серед коренів якого є число
-ого степеня, серед коренів якого є число ![]() ;
;
г) доведіть чи спростуйте твердження: число ![]() є коренем деякого многочлена з цілими коефіцієнтами.
є коренем деякого многочлена з цілими коефіцієнтами.
7) (Англія, 80) Знайти хоча б одну множину ![]() , що складається і семи послідовних натуральних чисел, для якої існує многочлен
, що складається і семи послідовних натуральних чисел, для якої існує многочлен ![]() п’ятого степеня з наступними властивостями:
п’ятого степеня з наступними властивостями:
а) всі коефіцієнти многочлена ![]() - цілі числа;
- цілі числа;
б) для п’яти чисел ![]() , включаючи найбільше і найменше, виконується рівність
, включаючи найбільше і найменше, виконується рівність ![]() ;
;
в) ![]() для одного числа
для одного числа ![]() .
.
Розв’язання. Множина ![]() і многочлен
і многочлен ![]() задовольняють всі умови задачі (при цьому умову б) виконано для
задовольняють всі умови задачі (при цьому умову б) виконано для ![]()
Теорема 7. Нехай ![]() і
і ![]() - деякі многочлени, причому
- деякі многочлени, причому ![]() . Тоді існують єдині многочлени
. Тоді існують єдині многочлени ![]() і
і ![]() , які задовольняють умовам:
, які задовольняють умовам:
1) ![]() , 2)
, 2) ![]() <
<![]() .
.
Тобто: многочлен ![]() при діленні на ненульовий многочлен
при діленні на ненульовий многочлен ![]() в частці дає многочлен
в частці дає многочлен ![]() ,
, ![]() - остача, причому
- остача, причому ![]() <
<![]() .
.
Якщо ![]() , то
, то ![]() , тобто
, тобто ![]() . [6] [7]
. [6] [7]
Завдання№3.
1) Знайти частку і остачу від ділення:
а) ![]() на
на ![]() ; б)
; б)![]() на
на ![]() ;
;
в) ![]() на
на ![]() ; г)
; г)![]() на
на ![]() ;
;
2) При якому значенні k виконується ділення без остачі многочлен ![]() на
на ![]() ?
?
3) При яких значеннях a і b многочлен ![]() ділиться без остачі на
ділиться без остачі на ![]() ?
?
2.3. Система вправ і задач з теми «Многочлени однієї змінної: теореми Безу та Вієта, алгоритм Евкліда» в шкільному курсі математики
2.3.1. Теорема Безу та наслідки з неї
Найбільш ефективним методом ділення многочлена ![]() на двочлен
на двочлен ![]() являється метод, який базується на теоремі Безу; схемі Горнера.
являється метод, який базується на теоремі Безу; схемі Горнера.
Означення. Нехай ![]() - даний многочлен степеня n,
- даний многочлен степеня n, ![]() - дане число, тоді
- дане число, тоді ![]() називається значенням цього многочленна в точці
називається значенням цього многочленна в точці ![]() .
.
Число ![]() називається коренем многочлена
називається коренем многочлена ![]() , якщо
, якщо ![]() .
.
Теорема Безу. Остача від ділення будь-якого многочлена ![]() на двочлен
на двочлен ![]() дорівнює значенню многочлена
дорівнює значенню многочлена ![]() при
при ![]() . [9]
. [9]
Доведення. Нехай ![]() – многочлен, що ділиться, а
– многочлен, що ділиться, а ![]() – дільник, тоді остача
– дільник, тоді остача ![]() або многочлен нульового степеню, або нуль, тобто
або многочлен нульового степеню, або нуль, тобто ![]() і тоді
і тоді ![]() звідси
звідси ![]() ,
, ![]() .
.
Наслідки:
-
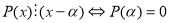 , тобто
, тобто 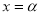 – корінь
– корінь 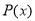 .
.
-
Якщо
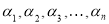 – різні корені многочлена
– різні корені многочлена 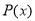 , то
, то 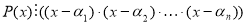 .
.
Доведення: доведемо м. м. і.
-
при
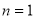 – твердження є правильним.
– твердження є правильним.
-
нехай твердження є правильним для
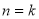 різних коренів і доведемо його для
різних коренів і доведемо його для 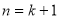 різних коренів. Нехай
різних коренів. Нехай 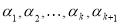 – різні корені многочлена
– різні корені многочлена 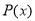 , тоді за припущенням:
, тоді за припущенням: 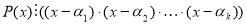 , тобто існує
, тобто існує 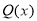 такий, що
такий, що 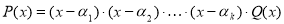 . Підставимо
. Підставимо 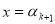 , отримаємо:
, отримаємо:
![]() , бо
, бо ![]() . І оскільки
. І оскільки ![]() , то
, то ![]() , звідси
, звідси ![]() , тобто
, тобто ![]() і
і ![]() .
.
- Число різних коренів многочлена, відмінного від нуля, не більше, ніж його степінь.
Доведення. Нехай ![]() і
і ![]() . Припустимо, що
. Припустимо, що ![]() має
має ![]() різних коренів
різних коренів ![]() , тоді за наслідком 2, отримаємо
, тоді за наслідком 2, отримаємо ![]() , що неможливо, оскільки степінь дільника не може бути більше степеня діленого.
, що неможливо, оскільки степінь дільника не може бути більше степеня діленого.
Означення. Число ![]() називається коренем многочлена
називається коренем многочлена ![]() кратності k, якщо
кратності k, якщо ![]() ділиться без остачі на
ділиться без остачі на ![]() але не ділиться на
але не ділиться на ![]() .
.
Приклади розв’язування вправ.
1. Не виконуючи ділення знайти остачу від ділення многочлена ![]() на квадратний тричлен
на квадратний тричлен ![]() .
.
Оскільки ![]() =(х-2)(х+1) і deg(R)<deg(Q), то R(x) – многочлен не вище першого степеня, тобто R(x)=ax+b. Тоді за теоремою про ділення многочленів:
=(х-2)(х+1) і deg(R)<deg(Q), то R(x) – многочлен не вище першого степеня, тобто R(x)=ax+b. Тоді за теоремою про ділення многочленів: ![]() ;
; ![]() , отже
, отже ![]() .
.
2. При якому ![]() виконується ділення без остачі многочлена
виконується ділення без остачі многочлена ![]() на х+4?
на х+4?
За теоремою Безу: Р(-4)=0, тоді![]() =0, звідки
=0, звідки ![]() =11.
=11.
3. При яких значеннях ![]() і
і ![]() виконується ділення без остачі многочлена
виконується ділення без остачі многочлена ![]() на
на ![]() ?
?
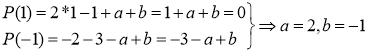 .
.
4. Знайдіть остачу від ділення многочлена ![]() на
на ![]() .
.
Остача являється многочленом степеня не вище першого. Інакше кажучи, ділення з остачею многочлена ![]() на
на ![]() приводить до наступного:
приводить до наступного: ![]() =
=![]() , де
, де ![]() - частка, а
- частка, а ![]() - остача. Знайдемо числа a і b. При
- остача. Знайдемо числа a і b. При ![]() з отриманої рівності маємо:
з отриманої рівності маємо: ![]() , а при
, а при ![]() :
: ![]() . Розв’язавши систему
. Розв’язавши систему 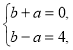 , знаходимо:
, знаходимо: ![]() . Отже, шукана остача має вигляд
. Отже, шукана остача має вигляд ![]() . [8]
. [8]
5. (Пекін, 63) Многочлен ![]() з цілими коефіцієнтами приймає значення 2 при чотирьох різних значеннях
з цілими коефіцієнтами приймає значення 2 при чотирьох різних значеннях ![]() . Довести, що ні при яких
. Довести, що ні при яких ![]() цей многочлен не приймає значень 1, 3, 5, 7 і 9.
цей многочлен не приймає значень 1, 3, 5, 7 і 9.
Розв’язання. Розглянемо многочлен ![]() і доведемо наступне твердження: якщо многочлен
і доведемо наступне твердження: якщо многочлен ![]() з цілими коефіцієнтами має 4 різні цілі корені, то при будь-якому значенні
з цілими коефіцієнтами має 4 різні цілі корені, то при будь-якому значенні ![]() ціле число
ціле число ![]() або рівне нулю, або є складеним (не може бути рівним 1). Нехай
або рівне нулю, або є складеним (не може бути рівним 1). Нехай ![]() – різні цілі корені многочлена
– різні цілі корені многочлена ![]() , тоді за теоремою Безу маємо розклад на множники
, тоді за теоремою Безу маємо розклад на множники ![]() деякий многочлен. Оскільки старший многочлена
деякий многочлен. Оскільки старший многочлена ![]() рівний 1, то многочлен
рівний 1, то многочлен ![]() має цілі коефіцієнти. Тоді число
має цілі коефіцієнти. Тоді число ![]() ціле, а число
ціле, а число ![]() ділиться на добуток
ділиться на добуток ![]() чотирьох різних цілих чисел, хоча б два з яких відмінні від 1 і -1. Тому або
чотирьох різних цілих чисел, хоча б два з яких відмінні від 1 і -1. Тому або ![]() , або число
, або число ![]() – складене. Тобто, при жодному значенні
– складене. Тобто, при жодному значенні ![]() число
число ![]() не рівне жодному з чисел -1, 1, 3, 5, 7, а значить
не рівне жодному з чисел -1, 1, 3, 5, 7, а значить ![]() не рівне жодному з чисел 1, 3, 5, 7 чи 9.
не рівне жодному з чисел 1, 3, 5, 7 чи 9.
Завдання №4.
1) (усно) Не виконуючи ділення, встановити, чи ділиться націло многочлен ![]() на многочлен
на многочлен ![]() :
:
а) ![]() ,
, ![]() ;
;
б) ![]() ,
, ![]() .
.
2) Знайти остачу від ділення многочлена ![]() на многочлен
на многочлен ![]() , використовуючи теорему Безу:
, використовуючи теорему Безу:
а) ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() ;
;
в) ![]() ,
, ![]() ;
;
г)![]() ; д)
; д) ![]() .
.
3) Многочлен ![]() при діленні
при діленні
а) на ![]() дає остачу 5, а при діленні на
дає остачу 5, а при діленні на ![]() - остачу 7. Яку остачу дає
- остачу 7. Яку остачу дає ![]() при діленні на
при діленні на ![]() ?
?
б) на ![]() дає остачу 4, а при діленні на
дає остачу 4, а при діленні на ![]() - остачу -1. Яку остачу дає
- остачу -1. Яку остачу дає ![]() при діленні на
при діленні на ![]() ?
?
в) на ![]() дає відповідно остачі 3, 15, 0. Знайти остачу від ділення
дає відповідно остачі 3, 15, 0. Знайти остачу від ділення ![]() на
на ![]() .
.
4) При яких значеннях ![]() і
і ![]() виконується ділення без остачі:
виконується ділення без остачі:
а) многочлена ![]() на
на ![]() ;
;
б) многочлена ![]() на
на ![]() ;
;
в) ![]() на
на ![]() ; г)
; г) ![]() на
на ![]() ; д)
; д) ![]() на
на ![]() ?
?
5) При яких значеннях а і b
а) многочлен ![]() ділиться без остачі на
ділиться без остачі на ![]() , а при діленні на
, а при діленні на ![]() дає остачу
дає остачу ![]() ;
;
б) многочлен ![]() ділиться без остачі на
ділиться без остачі на ![]() , а при діленні на
, а при діленні на ![]() дає остачу
дає остачу ![]() ?
?
6) При діленні ![]() на
на ![]() одержано остачу
одержано остачу ![]() . Якою буде остача від ділення
. Якою буде остача від ділення ![]() на
на ![]() , якщо
, якщо ![]() ?
?
7) Знайти:
а) многочлен третього степеня, який має корені 1, -1, 2;
б) многочлен четвертого степеня, який має однократні корені 1, 3 і двократний корінь 1;
в) кубічний многочлен, який має корінь кратності 2 – число 3 і корінь -1, а старший коефіцієнт дорівнює 2.
8) (Нью-Йорк, 73; Бельгія, 81) Довести, що для будь-якого значення ![]() , многочлен
, многочлен ![]()
9) (США, 77) Знайти всі пари чисел ![]() , для яких многочлен
, для яких многочлен ![]() ділиться на многочлен
ділиться на многочлен ![]() .
.
2.3.2. Схема Горнера
Схема Горнера дає можливість знаходити частку, остачу від ділення многочлена на лінійний двочлен. Особливо зручна, коли отриману частку знову треба ділити на лінійний двочлен. Якщо ![]() слід поділити на
слід поділити на ![]() , то коефіцієнти частки
, то коефіцієнти частки ![]() і остача
і остача ![]() знаходяться за таблицею (зауважимо: степінь частки на один менше за степінь остачі):
знаходяться за таблицею (зауважимо: степінь частки на один менше за степінь остачі):
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
Приклади розв’язування вправ
1. Поділити многочлен ![]() на двочлен
на двочлен ![]() і знайдену неповну частку поділити на
і знайдену неповну частку поділити на ![]()
|
|
1 |
0 |
-3 |
2 |
-1 |
|
|
2 |
1 |
|
|
|
|
степінь частки=3 |
|
2 |
1 |
|
|
|
Степінь частки=2 |
|
2. Встановити кратність кореня ![]() для многочлена
для многочлена ![]() . Розкласти даний многочлен на множники.
. Розкласти даний многочлен на множники.
|
|
1 |
3 |
-6 |
-28 |
-24 |
|
-2 |
1 |
1 |
-8 |
-12 |
0 |
|
-2 |
1 |
-1 |
-6 |
0 |
|
|
-2 |
1 |
-3 |
0 |
||
|
3 |
1 |
0 |
|||
Отже, кратність кореня ![]() даного многочлена дорівнює трьом і
даного многочлена дорівнює трьом і ![]() .
.
Завдання №5
1) Знайти частку і остачу від ділення наступних пар многочленів:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ;
;
в) ![]() і
і ![]() ; г)
; г) ![]() і
і ![]() .
.
2) Знайти кратність кореня ![]() для многочлена
для многочлена ![]() та розкласти його на множники:
та розкласти його на множники:
а) ![]()
![]() ; б)
; б) ![]() .
.
2.3.3. Теорема про раціональний корінь многочлена
Розглянемо елементарний спосіб знаходження раціональних коренів многочлена з раціональними коефіцієнтами. Зауважимо, що будь-який многочлен ![]() з раціональними коефіцієнтами
з раціональними коефіцієнтами ![]() легко зводиться до многочлена з цілими коефіцієнтами шляхом множення рівняння
легко зводиться до многочлена з цілими коефіцієнтами шляхом множення рівняння ![]() на спільний знаменник усіх коефіцієнтів
на спільний знаменник усіх коефіцієнтів ![]() .
.
Теорема про раціональний корінь многочлена. Якщо нескоротний раціональний дріб ![]() є коренем многочлена
є коренем многочлена ![]() з цілими коефіцієнтами, то
з цілими коефіцієнтами, то ![]() і
і ![]() .
.
Доведення. Нехай нескоротний раціональний дріб ![]() є коренем многочлена
є коренем многочлена ![]() . Нескоротний означає: НСД (p; q)=1, тобто p не ділиться на q і q не ділиться на p.
. Нескоротний означає: НСД (p; q)=1, тобто p не ділиться на q і q не ділиться на p. 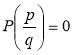 , тобто
, тобто 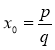 - корінь многочлена
- корінь многочлена ![]() . З того, що
. З того, що 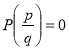 слідує
слідує 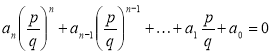 ,
, ![]() (*).
(*).
Запишемо рівність (*) так: ![]() , видно, що права частина ділиться на q, а тому
, видно, що права частина ділиться на q, а тому ![]() ( оскільки p не ділиться на q). Запишемо (*) по-іншому:
( оскільки p не ділиться на q). Запишемо (*) по-іншому: ![]() , де ліва частина ділиться на p, тоді
, де ліва частина ділиться на p, тоді ![]() (оскільки q не ділиться на p).
(оскільки q не ділиться на p).
Наслідки
- Будь-який цілий корінь многочлена з цілими коефіцієнтами є дільником вільного члена.
-
Якщо
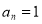 , то всі раціональні корені многочлена
, то всі раціональні корені многочлена 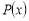 (якщо вони існують) є цілими числами.
(якщо вони існують) є цілими числами.
-
Зведений многочлен
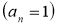 не має дробових коренів.
не має дробових коренів.
Якщо многочлен ![]() з цілими коефіцієнтами не має коренів виду
з цілими коефіцієнтами не має коренів виду ![]() , що
, що ![]() і
і ![]() , то такий многочлен не має раціональних коренів. [15] [16] [17]
, то такий многочлен не має раціональних коренів. [15] [16] [17]
Приклади розв’язування вправ
-
Знайти всі цілі корені многочлена
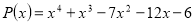 .
.
Оскільки цілі корені многочлена знаходяться серед дільників вільного члена, тобто цілими дільниками числа -6 є числа: ![]() , то перевіримо ці числа на корені:
, то перевіримо ці числа на корені:
![]() .
.
Отже, ![]() - всі цілі корені даного многочлена.
- всі цілі корені даного многочлена.
-
Знайти всі раціональні корені многочлена
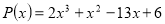 .
.
Згідно до теореми про раціональний корінь многочлена, раціональний корінь даного многочлена ![]() такий, що
такий, що ![]() і
і ![]() , де
, де ![]() , тому шуканий корінь
, тому шуканий корінь ![]() складено з дільників чисел 6 і 2, а отже його слід шукати серед чисел:
складено з дільників чисел 6 і 2, а отже його слід шукати серед чисел: ![]() ,
,![]() . Порівнюючи з нулем
. Порівнюючи з нулем ![]() , отримаємо, що
, отримаємо, що ![]()
![]() - шукані корені.
- шукані корені.
- (Англія, 78) Довести, що:
а) для будь-якого ![]() існує многочлен
існує многочлен ![]() з цілими коефіцієнтами, що задовольняє рівність
з цілими коефіцієнтами, що задовольняє рівність ![]()
б) для будь-якого ![]() число
число ![]() або співпадає з одним із чисел
або співпадає з одним із чисел ![]() , або ірраціональне.
, або ірраціональне.
Розв’язання. а) Позначимо ![]()
![]() .
.
Поклавши у формулі ![]() значення
значення ![]() рівним спочатку 2, потім 3 і т.д. знайдемо спочатку многочлен
рівним спочатку 2, потім 3 і т.д. знайдемо спочатку многочлен ![]() , потім
, потім ![]() і т.д. Зауважимо, що старший коефіцієнт будь-якого із многочленів
і т.д. Зауважимо, що старший коефіцієнт будь-якого із многочленів ![]()
б) Нехай ![]() , де m
, де m![]() ,
, ![]() , і дріб
, і дріб ![]() – нескоротний. Тоді величина
– нескоротний. Тоді величина ![]() рівний або 2 або -2. В силу доведеного вище твердження, а) величину
рівний або 2 або -2. В силу доведеного вище твердження, а) величину ![]() можна представити у вигляді многочлена
можна представити у вигляді многочлена ![]() з цілими коефіцієнтами від змінної
з цілими коефіцієнтами від змінної ![]() . Тоді число
. Тоді число ![]() є коренем многочлена
є коренем многочлена ![]() у якого всі коєфіцієнти цілі, а ккоефіцієнт при старшому члені рівний 1. Тому число
у якого всі коєфіцієнти цілі, а ккоефіцієнт при старшому члені рівний 1. Тому число ![]() може бути або цілим, або ірраціональним. Нехай
може бути або цілим, або ірраціональним. Нехай ![]() – ціле число. Оскільки
– ціле число. Оскільки ![]() , то воно дорівнює одному з чисел
, то воно дорівнює одному з чисел ![]() . Отримаємо, що якщо число
. Отримаємо, що якщо число ![]() раціональне (де
раціональне (де ![]() , то воно рівне одному з чисел
, то воно рівне одному з чисел ![]() .
.
Завдання №6
1) Знайти всі цілі корені многочлена. Розкласти многочлен на множники:
а)![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)![]() ; д)
; д)![]() ; е)
; е) ![]() ;
;
2) Знайти всі раціональні корені многочлена. Розкласти многочлен на множники: а) ![]() ; б)
; б) ![]() ;
;
в)![]() ; г)
; г) ![]() .
.
2.3.4. Теорема Вієта. Узагальнена теорема Вієта
Нехай зведений многочлен третього степеня ![]() має три дійсні корені
має три дійсні корені ![]() , тоді кожен двочлен
, тоді кожен двочлен ![]() являється дільником даного многочлена і
являється дільником даного многочлена і ![]()
![]() .
.
Прирівняємо коефіцієнти лівої і правої частин: 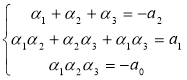 (1)
(1)
Отже, якщо числа ![]() - корені многочлена третього степеня
- корені многочлена третього степеня ![]() , то виконується система (1) – теорема Вієта для зведеного многочлена третього степеня.
, то виконується система (1) – теорема Вієта для зведеного многочлена третього степеня.
Обернене твердження пропонується встановити самостійно.
Теорема (Вієта): Якщо ![]() - корені многочлена
- корені многочлена ![]() , то
, то 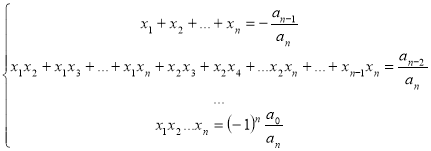 [13]
[13]
Приклади розв’язування вправ
1. Знайти многочлен третього степеня, що має корінь 2 і корінь -1 другої кратності.
Нехай шуканий многочлен має вигляд ![]() . Згідно теоремі Вієта:
. Згідно теоремі Вієта: 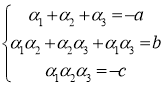 , тобто
, тобто 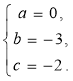
Отже, шуканий многочлен має вигляд: ![]()
2. При яких значеннях параметра а многочлен ![]() має кратні корені? Знайти їх.
має кратні корені? Знайти їх.
Згідно теоремі Вієта: 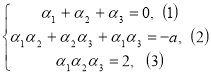 Коренів може бути всього три, то якщо існує кратний корінь, то його кратність 2 чи 3. Якщо кратність кореня дорівнює 3
Коренів може бути всього три, то якщо існує кратний корінь, то його кратність 2 чи 3. Якщо кратність кореня дорівнює 3 ![]() , тоді рівняння (1) несумісне з (3); якщо кратність кореня дорівнює 2
, тоді рівняння (1) несумісне з (3); якщо кратність кореня дорівнює 2 ![]() :
: 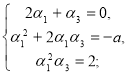 звідки
звідки ![]()
3. Розв’язати систему рівнянь 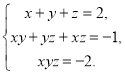
Згідно до теореми, оберненої до теореми Вієта, числа ![]() являються коренями многочлена третього степеня
являються коренями многочлена третього степеня ![]() , а саме
, а саме ![]() - корені многочлена, а отже розв’язками даної системи є трійки чисел (-1;1;2), (1;-1;2), (2;-1;1), (2;1;-1), (-1;2;1), (1;2;-1).
- корені многочлена, а отже розв’язками даної системи є трійки чисел (-1;1;2), (1;-1;2), (2;-1;1), (2;1;-1), (-1;2;1), (1;2;-1).
Завдання №7
1) Знайти многочлен третього степеня, що має корені 1; -1; -2.
2) Знайти многочлен четвертого степеня, що має один двократний корінь 1 і два корені -1 і 3.
3) Знайти спільні корені многочленів ![]() і
і ![]()
4) Не розв’язуючи рівняння ![]() , знайти:
, знайти:
а) ![]() ; б)
; б) ![]() , де
, де ![]() - корені даного рівняння.
- корені даного рівняння.
5) Один з коренів многочлена ![]() в два рази більше другого. Знайти а і корені многочлена.
в два рази більше другого. Знайти а і корені многочлена.
6) Корені многочлена ![]() утворюють арифметичну прогресію. Знайти
утворюють арифметичну прогресію. Знайти ![]() та його корені, якщо: а)
та його корені, якщо: а) ![]() ; б)
; б) ![]() .
.
7) Розв’язати систему рівнянь:
а) 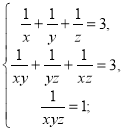 б)
б) 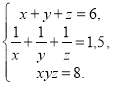 в)
в) 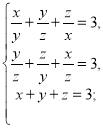 г)
г)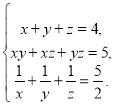 [14]
[14]
Запрошуємо до розгляду пошуково-дослідницьких задач.
1. Чи існує натуральне число ![]() і такий відмінний від константи многочлен
і такий відмінний від константи многочлен ![]() з цілими коефіцієнтами, що кожні два з чисел
з цілими коефіцієнтами, що кожні два з чисел ![]() взаємно прості?
взаємно прості?
2. Доведіть або спростуйте твердження: число ![]() є коренем деякого многочлена з цілими коефіцієнтами.
є коренем деякого многочлена з цілими коефіцієнтами.
3. Позначимо через ![]() суму добутків по
суму добутків по ![]() чисел від 1 до n. Наприклад,
чисел від 1 до n. Наприклад, ![]() .
.
а) Знайдіть формули для ![]() і
і ![]() .
.
б) Доведіть, що ![]() є многочленом від
є многочленом від ![]() степеня
степеня ![]() .
.
в) Вкажіть метод знаходження многочленів ![]() при
при ![]() та використайте його для знаходження многочленів
та використайте його для знаходження многочленів ![]() і
і ![]() .
.
2.4 Система вправ і задач з теми «Функціональні співвідношення у класі многочленів» в шкільному курсі математики.
Як відомо, що многочленом (поліномом) називається функція виду ![]() де
де ![]() – будь-які дійсні числа. Тому під функціональними співвідношеннями у класі многочленів будемо розуміти рівність, в яких шукана функція – многочлен пов’язана з відомими функціями – многочленами за допомогою арифметичних дій та операції утворення складеної функції. При цьому під розв’язком такого співвідношення будемо розуміти многочлен, який на заданій множині перетворює його у тотожність.
– будь-які дійсні числа. Тому під функціональними співвідношеннями у класі многочленів будемо розуміти рівність, в яких шукана функція – многочлен пов’язана з відомими функціями – многочленами за допомогою арифметичних дій та операції утворення складеної функції. При цьому під розв’язком такого співвідношення будемо розуміти многочлен, який на заданій множині перетворює його у тотожність.
Вивчення теми «Функціональних співвідношень у класі многочленів» передбачає наступні педагогічні задачі:
– поглибити та розвинути сформовані раніше знання з теми многочлени;
- ознайомити з основними прийомами розв’язування функціональних співвідношень;
- підготувати учнів до участі в олімпіадах та конкурсах;
- активізувати навчально-пізнавальну та пошуково-дослідницьку діяльності учнів;
- посилити прикладну спрямовагість курсу математики та підвищення фундаментальної математичної підготовки.
Перед викладенням матеріалу з даної теми, вчитель повинен ґрунтовно підготувати матеріал, а саме дібрати завдання, для повторення та закріплення знань перед викладанням нової теми, дібрати задачі та систему вправ, які будуть зрозумілі широкій аудиторії, для учнів різного рівня знань. Тому виникає важливе питання не тільки в методиці викладання математики середньої школи, а й в методиці викладання математики позашкільних занять: яким оптимальним підбором вправ можна досягнути цілісного та міцного засвоєння знань? Система задач повинна давати приклади отримання одного й того ж результату різноманітними шляхами й спонукати учня до подібних самостійних дій, до самостійного розв’язання задач прикладного характеру, розвитку пошукових та дослідницьких здібностей, гнучкості й критичності мислення [18].
Розглянемо найбільш виразні із складеної системи задач на функціональні співвідношення для многочленів, що пропонувалися на змаганнях різного рівня.
- Знайти всі многочлени, які є одночасно парними і непарними функціями.
Розв’язання. Оскільки єдиною одночасно і парною і непарною являється функція![]() =0, або многочлен нульового степеню
=0, або многочлен нульового степеню ![]() .
.
-
Нехай многочлен
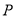 такий, що для всіх
такий, що для всіх 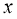 виконується рівність
виконується рівність 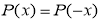 . Чи може
. Чи може 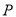 містити непарні степені
містити непарні степені 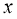 ?
?
-
Серед многочленів виду
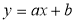 знайти всі такі, що для всіх
знайти всі такі, що для всіх 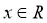 виконується рівність: а)
виконується рівність: а) 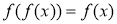 ; б)
; б)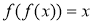 .
.
Розв’язання. а) Оскільки ![]() , то маємо тотожність
, то маємо тотожність ![]() або
або ![]() звідси
звідси 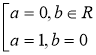 . Значить,
. Значить, ![]() або
або ![]() .
.
б) Згідно а) маємо : ![]() або
або ![]() звідси
звідси ![]() . Значить,
. Значить, ![]() або
або ![]() .
.
-
Нехай
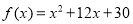 . Розв’язати рівняння
. Розв’язати рівняння 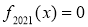 . Тут
. Тут 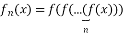
Розв’язання. Зауважимо, що ![]() , а тоді знаходимо
, а тоді знаходимо![]() ,
, ![]() . Методом
. Методом
математичної індукції легко довести, що ![]() . Отже, рівняння
. Отже, рівняння ![]() рівносильне такому:
рівносильне такому: ![]() , звідки
, звідки ![]() , а
, а ![]() і
і ![]() ,
, ![]() .
.
Після розв’язання такої задачі логічно запропонувати самостійно розглянути наступну задачу:
-
Чи існують такі дійсне число
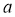 і многочлен
і многочлен 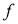 , що
, що 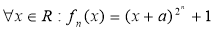 ?
?
Відповідь: так. Наприклад, ![]() задовольняє умову, тут
задовольняє умову, тут ![]() . Дійсно, якщо
. Дійсно, якщо ![]() , то легко довести м. м. і., що
, то легко довести м. м. і., що ![]() .
.
-
Нехай маємо многочлен
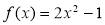 . Розв’язати рівняння
. Розв’язати рівняння 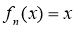 .
.
Розв’язання. Зауважимо, що корені вихідного рівняння слід шукати на проміжку ![]() , бо при
, бо при ![]() матимемо
матимемо ![]() - протиріччя. Отже, можемо покласти, що
- протиріччя. Отже, можемо покласти, що ![]() для деякого
для деякого ![]() . При
. При ![]()
![]() і
і ![]() , а
, а ![]() (це легко довести м. м. і.). Таким чином, рівняння
(це легко довести м. м. і.). Таким чином, рівняння ![]() рівносильне такому:
рівносильне такому: ![]() , а з останнього випливає:
, а з останнього випливає: ![]() , тобто
, тобто ![]() і
і ![]() , а відповідно
, а відповідно ![]() . Аналогічно розв’язується наступна задача.
. Аналогічно розв’язується наступна задача.
-
Нехай маємо многочлен
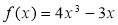 . Розв’язати рівняння
. Розв’язати рівняння 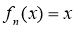 .
.
-
Знайти многочлен
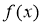 , якщо
, якщо 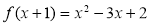 .
.
Розв’язання. Якщо ![]() , то позначивши
, то позначивши ![]() , тобто
, тобто ![]() , отримаємо:
, отримаємо: ![]() . Отже,
. Отже, ![]() .
.
9. Знайти многочлен ![]() , якщо
, якщо ![]() .
.
Розв’язання. Якщо ![]() , то при
, то при ![]() будемо мати
будемо мати ![]() , а при
, а при ![]() , остаточно отримаємо
, остаточно отримаємо ![]() .
.
10. Знайдіть усі многочлени ![]() з дійсними коефіцієнтами, для яких при всіх
з дійсними коефіцієнтами, для яких при всіх ![]() одночасно виконуються дві нерівності:
одночасно виконуються дві нерівності: ![]() і
і ![]() .
.
11. (ГДР, 74) а) Довести, що не існуі многочлена ![]() , для якого при будь-якому
, для якого при будь-якому ![]() виконується нерівність 1)
виконується нерівність 1) ![]() ; 2)
; 2) ![]() ; б) чи справджуватиметься твердження а), якщо нерівність 1) замінити на нерівність
; б) чи справджуватиметься твердження а), якщо нерівність 1) замінити на нерівність ![]() )
) ![]() ?
?
Розв’язання. а) Якщо ![]() – константа, то
– константа, то ![]() і нерівність 1) не виконано. Нехай
і нерівність 1) не виконано. Нехай ![]() . Тоді якщо
. Тоді якщо ![]() – непарне, то
– непарне, то ![]() хоча б в одній точці
хоча б в одній точці ![]() , якщо ж
, якщо ж ![]() – парне, то
– парне, то ![]() – непарне число, звідки
– непарне число, звідки ![]() хоча б в одній точці
хоча б в одній точці ![]() . Таким чином, для многочлена
. Таким чином, для многочлена ![]() не виконано або нерівність 1), або нерівність 2). Твердження 2) доведено.
не виконано або нерівність 1), або нерівність 2). Твердження 2) доведено.
б) Покладемо, ![]() . Тоді для всіх
. Тоді для всіх ![]() маємо:
маємо: ![]() ,
, ![]() , тобто відповідь на питання п.б) – негативна.
, тобто відповідь на питання п.б) – негативна.
11. Про многочлени з цілими коефіцієнтами ![]() відомо, що многочлен
відомо, що многочлен ![]() ділиться без остачі на многочлен
ділиться без остачі на многочлен ![]() Знайдіть
Знайдіть ![]()
Розв’язання. Відомо, що якщо многочлен ![]() з цілими коефіцієнтами і
з цілими коефіцієнтами і ![]() , то
, то ![]() . Тому для цілого х:
. Тому для цілого х: ![]()
Значить вираз
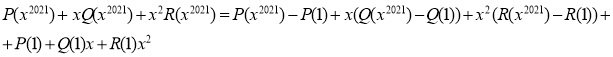 ділиться без остачі на многочлен
ділиться без остачі на многочлен ![]() Але
Але ![]() тому многочлен
тому многочлен ![]() має ділитися теж націло на
має ділитися теж націло на ![]()
Останнє можливо, коли многочлен![]() є нуль – многочленом, бо степінь многочлена
є нуль – многочленом, бо степінь многочлена ![]() дорівнює 2020. Отже,
дорівнює 2020. Отже, ![]() звідки
звідки ![]()
Завдання для самостійного опрацювання.
1. Знайти![]() , якщо
, якщо ![]() .
.
2. Нехай ![]() . Розв’язати рівняння
. Розв’язати рівняння ![]() .
.
3. Чи існує многочлен ![]() , що
, що ![]() задовольняє умові:
задовольняє умові:
![]() ?
?
4. Нехай ![]() , а
, а ![]() . Доведіть, що корені рівняння
. Доведіть, що корені рівняння ![]()
![]() дійсні і різні.
дійсні і різні.
5. Знайти многочлен: 1) ![]() , якщо
, якщо ![]() , 2)
, 2) ![]() , якщо
, якщо ![]() .
.
6. Нехай ![]() – а) квадратний тричлен; б) многочлен парного степеня з невід’ємними коефіцієнтами. Доведіть нерівність:
– а) квадратний тричлен; б) многочлен парного степеня з невід’ємними коефіцієнтами. Доведіть нерівність: ![]()
![]() .
.
7. Нехай ![]() – многочлен такий, що для кожного многочлена
– многочлен такий, що для кожного многочлена ![]() має місце функціональне співвідношення:
має місце функціональне співвідношення: ![]() . Знайти
. Знайти ![]() .
.
8. (США, 76) Нехай многочлени ![]() ,
, ![]() ,
, ![]() та
та ![]() задовольняють рівність
задовольняють рівність ![]()
Довести, що многочлен ![]() ділиться на многочлен
ділиться на многочлен ![]() .
.
Запрошуємо до розгляду пошуково-дослідницьких задач
-
Знайдіть усі многочлени
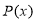 з дійсними коефіцієнтами, для яких при всіх
з дійсними коефіцієнтами, для яких при всіх 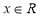 одночасно виконуються дві нерівності:
одночасно виконуються дві нерівності: 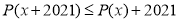 і
і  .
.
-
Чи існує такий многочлен
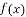 другого степеня, що для будь-якого
другого степеня, що для будь-якого 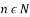 рівняння
рівняння 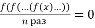 , має рівно
, має рівно 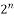 розв’язки?
розв’язки?
-
Нехай
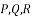 – многочлени, причому степені многочленів
– многочлени, причому степені многочленів 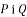 різні і додатні.
різні і додатні.
а) Доведіть, що ![]() існує не більше одного многочлена
існує не більше одного многочлена ![]() степеня
степеня ![]() зі старшим коефіцієнтом 1 такого, що
зі старшим коефіцієнтом 1 такого, що ![]() .
.
б) Знайдіть хоча б один такий, відмінний від константи, многочлен ![]() , що
, що ![]() [19].
[19].
Запрошуємо до розгляду відкритих проблем.
Цікаву проблему про значення многочленів запропонували О. Г. Кукуш та Р. П. Ушаков [21]: Зафіксуємо натуральне число ![]() .
.
Означення. Многочлен ![]() з цілими коефіцієнтами називається m-подільним, якщо при будь-якому цілому k число
з цілими коефіцієнтами називається m-подільним, якщо при будь-якому цілому k число ![]() ділиться на m без остачі.
ділиться на m без остачі.
Приклад. ![]() ,
, ![]() ,
, ![]() . Многочлен
. Многочлен ![]() є також 6-подільним, а многочлен
є також 6-подільним, а многочлен ![]() є m-подільним при
є m-подільним при ![]() та
та ![]() Легко бачити, що при будь-якому
Легко бачити, що при будь-якому ![]() многочлен
многочлен ![]() є m-подільним.
є m-подільним.
Теорема. Нехай є m – просте число, тоді ![]() є m-подільним.
є m-подільним.
Доведення: Якщо ![]() ,
, ![]() , то
, то ![]() , ділиться на m. Якщо ж
, ділиться на m. Якщо ж ![]() ,
, ![]() , то числа k та m взаємно прості і згідно з малою теоремою Ферма
, то числа k та m взаємно прості і згідно з малою теоремою Ферма ![]() ділиться на m. Тут
ділиться на m. Тут ![]() – це функція Ейлера, вона дорівнює кількості натуральних чисел, менших за m та взаємно простих з ним. Для простого m
– це функція Ейлера, вона дорівнює кількості натуральних чисел, менших за m та взаємно простих з ним. Для простого m ![]() . То при
. То при ![]()
![]() .
.
Пропонується проблема: для довільного натурального ![]() якомога точніше оцінити зверху та знизу найменший степінь m-подільного многочлена з взаємно простими коефіцієнтами (цілі числа
якомога точніше оцінити зверху та знизу найменший степінь m-подільного многочлена з взаємно простими коефіцієнтами (цілі числа ![]() називаються взаємно простими, якщо їх найбільший спільний дільник дорівнює 1).
називаються взаємно простими, якщо їх найбільший спільний дільник дорівнює 1).
Зокрема можна довести, що для простого числа m цей степінь рівний m.
Проблема С. Конягіна та деякі задачі
Розглянемо цикл задач, який містить одну нерозв’язану проблему, поставлену С. Конягіним. Цей цикл пропонувався на шостій літній конференції Турніру міст, яка відбулась у 1994 р. у м. Білорєцькому.
Загальна задача (розв’язання невідоме). Нехай ![]() – довільний многочлен з цілими коефіцієнтами. Розглянемо таку умову
– довільний многочлен з цілими коефіцієнтами. Розглянемо таку умову ![]() , яка залежить від
, яка залежить від ![]() :
: ![]()
![]() ділить
ділить 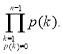
Гіпотеза. Для будь-якого многочлена ![]() існує нескінченно багато таких
існує нескінченно багато таких ![]() , що
, що ![]() виконується.
виконується.
Розгляньте такі задачі:
- Розв’язати задачу для таких частинних випадків:
а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() .
.
-
Якщо просте число
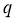 ділить
ділить 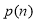 і
і 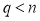 , то
, то 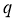 ділить також
ділить також 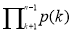 .
.
-
Якщо
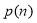 розкладається на прості множники, які менші
розкладається на прості множники, які менші 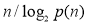 , то
, то 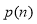 ділить
ділить 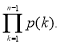
-
Довести, що
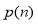 ділить
ділить 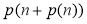 .
.
- Довести гіпотезу для многочленів:
а) ![]() ; б)
; б)![]() ; в)
; в)![]() .
.
Для яких ще многочленів Ви можете встановити справедливість гіпотези?
-
«Обернена задача». Довести, що існує нескінченно багато таких натуральних
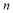 , що умова
, що умова 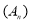 не виконується.
не виконується.
Запропонована система задач з функціональних співвідношень у класі многочленів відповідає наступним принципам: принцип повторення та послідовного зростання складності (задачі №1- №4); принцип диференціації та різноманітності; принцип доступності та однотипності (№4-5, №6-7, №8-9); принцип внутрішніх зв’язків; принцип міжпредметних, міжнаукових зв’язків та виконання задач творчого характеру (це задачі № 6,7; задачі із рубрики «Запрошуємо до розгляду пошуково-дослідницьких задач» та «Запрошуємо до розгляду відкритих проблем», які можна пропонувати учням – кандидатам Малої академії наук).
Зазначимо, що вище зазначені задачі не просто цікаві, розв’язування деяких з них надзвичайно красиві і не виходять за рамки шкільної програми, оскільки можуть бути розв’язані шкільними методами. Тому вивчення школярами даної тематики покращує закріплення пройденого матеріалу, сприяє розвитку інтересу до предмета, дозволяє відпрацювати різні способи розв’язування задач при підготовці до змагань, олімпіад різного рівня.
2.5 Система вправ і задач з теми «Функціональні рівняння у класі многочленів» в шкільному курсі математики.
Мова піде про рівняння, де в ролі невідомих виступають функції.
Означення. Функціональним рівнянням називають рівність, до складу якої входить незалежна змінна і невідома функція цієї змінної.
Наприклад, рівності виду: ![]() ,
,![]() є функціональними рівняннями з невідомою функцією
є функціональними рівняннями з невідомою функцією ![]() .
.
Функціональні рівняння можна розглядати як ще один спосіб задання функції, а саме задання функції як розв’язку функціонального рівняння. В таких рівняннях шукані функції пов’язані з відомими за допомогою операцій утворення складених функцій. Розрізняють частинний та загальний розв’язки функціонального рівняння. Частинний розв’язок функціонального рівняння - є функція або система функцій, яка задовольняє рівнянню в заданій області визначення. Загальний розв’язок складає сукупність усіх функцій, які задовольняють рівняння. Будь-який розв’язок функціонального рівняння залежить від того, в якому класі функцій воно розв’язується (в класі обмежених, неперервних, диференційованих тощо) [20].
Теоретичні й практичні застосування саме таких рівнянь спонукали видатних математиків до їхнього вивчення. Досить лише навести рівняння Коші ![]() яке використовується у проективній геометрії і теорії ймовірностей.
яке використовується у проективній геометрії і теорії ймовірностей.
Вивчення теми “Функціональні рівняння” в курсі математики передбачають вирішення таких педагогічних задач як і при вивченні теми “Функціональні співвідношення”, які описані в попередньому пункті. Проаналізувавши психолого-педагогічну, методичну, дидактичну та наукову літератури та з особистого досвіду роботи можна реалізувати методику роботи, що представлена нижче.
Але перед тим як розпочинати розгляд основних методів розв’язання функціональних рівнянь в класі многочленів, розглянемо такого плану задачі:
Задача1. Покажіть, що многочлен ![]() задовольняє заданому функціональному рівнянню
задовольняє заданому функціональному рівнянню ![]() .
.
Розв’язання. Якщо ![]() , то
, то ![]() , а
, а ![]() , а отже,
, а отже, ![]() .
.
Значить, функція ![]() задовольняє рівнянню
задовольняє рівнянню![]() .
.
Задача 2. При яких a многочлен ![]() буде розв’язком функціонального рівняння
буде розв’язком функціонального рівняння ![]() .
.
Розв’язання. Припустимо, що функція ![]() є розв’язком заданого функціонального рівняння, тоді
є розв’язком заданого функціонального рівняння, тоді ![]() a
a ![]() .
.
Підставляючи останній вираз у вихідне рівняння, матимемо тотожність:
![]() , звідки
, звідки ![]() . Отже,
. Отже, ![]() буде розв’язком рівняння.
буде розв’язком рівняння.
Таким чином, для першого знайомства вибрали такі задачі, які задовольняють таким вимогам:
- задача не є складною і для її розв’язання використано достатньо мінімальні теоретичні відомості;
- формулювання задачі спрямоване не тільки на закріплення поняття про розв’язок функціонального рівняння, а і на розкриття ідеї одного із майбутніх методів розв’язання функціональних рівнянь.
Постає питання: як же знайти розв’язки певного функціонального рівняння в класі многочленів?
На це питання нам може відповісти один із найпоширеніших методів – метод підстановок, який дозволяє у своїй більшості розв’язати функціональне рівняння без суттєвих обмежень, а до того ж є достатньо елементарним та метод невизначених коефіцієнтів, особливо ефективний при розв’язуванні функціональних рівнянь у класі многочленів
Задача 3. Знайти всі многочлени з дійсними коефіцієнтами, для яких виконується рівність![]() для всіх
для всіх ![]() .
.
Розв'язання: Оскільки в лівій частині рівняння над незалежною змінною![]() і значеннями
і значеннями ![]() виконуються лише лінійні операції, а правою частиною рівняння є многочлен другого степеня, то логічно припустити, що шуканий многочлен має вигляд:
виконуються лише лінійні операції, а правою частиною рівняння є многочлен другого степеня, то логічно припустити, що шуканий многочлен має вигляд: ![]() де
де ![]() - коефіцієнти, які підлягають визначенню, тобто невизначені коефіцієнти. З того, що ця функція має бути розв’язком рівняння, випливає тотожність
- коефіцієнти, які підлягають визначенню, тобто невизначені коефіцієнти. З того, що ця функція має бути розв’язком рівняння, випливає тотожність ![]() , яка після виконання перетворень у лівій частині, набуває вигляду 3
, яка після виконання перетворень у лівій частині, набуває вигляду 3

про публікацію авторської розробки
Додати розробку


