Урок узагальнення і систематизація знань з теми" Нерівності"
|
Конспект уроку з алгебри 9 клас
Підготувала Вчитель математики 9 класу Лосківської зош І-ІІ ст.. Пузан Галина Олександрівна |
Тема уроку: «Нерівності»
Мета уроку: Узагальнити і систематизувати знання учнів по темі «Нерівності».
Формувати в учнів вміння встановлювати головне, самостійно застосувати набуті знання в стандартних і нестандартних ситуаціях, а також уміти систематизувати певні математичні твердження, робити висновки.
Розвивати логічне мислення. Розвивати почуття краси в математиці.
Обладнання: мультимедійний проектор, презентація «Нерівності»
Хід уроку
- Повідомлення теми, мети і завдань уроку, мотивація учіння школярів.
Учитель: Сьогоднішній урок я хочу розпочати висловом «У математиці є своя краса, як у поезії і музиці». Тема нашого уроку: «Узагальнення і систематизація знань учнів по темі «Нерівності». Я думаю, що на цьому уроці ми розкриємо красу математичних закономірностей, покажемо творчість і досконалість математичної мови при повторенні питань даної теми: «Розв’язування нерівностей; нерівності, які містять змінну під знаком модуля, лінійні нерівності з параметром, доведення нерівностей». Тема дуже важлива, сьогоднішній знання потрібні і далі при вивчені математики. Про це ви самі переконаєтесь на сьогоднішньому уроці.
Розпочнемо з перевірки домашнього завдання.
Вчитель: Що було задано додому?
Домашнє завдання:
1) Яке найбільше натуральне n задовольняє нерівність ![]() ,
,![]() n = 4.
n = 4.
2) Розв’язати подвійну нерівність:
![]()
![]()
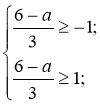
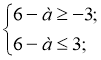
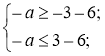
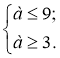
Відповідь: [3; 9].
б) ![]()
Відповідь: 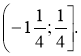
- Довести нерівність:
(а+b)(ab+1)![]() 4ab, якщо а
4ab, якщо а![]() 0; b
0; b![]() 0.
0.
Доведення.
![]() .
.
(середнє арифметичне не перевищує середнє геометричне)
Перемножимо нерівності і одержимо результат. ![]()
- Розв’язати нерівність:
![]() .
.
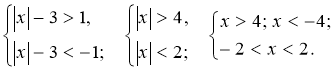
Якщо немає питань до домашнього завдання, то перейдемо до наступного кроку нашого уроку по даній темі «Нерівності».
- Відтворення та узагальнення понять та засвоєння відповідної їм системи знань.
Експрес-опитування (учень формулює запитання і вказує, хто на нього відповідає).
Питання:
- Який спосіб використовують в математиці для порівняння чисел? (складають різницю чисел і з’ясовують, буде вона додатним, від’ємним числом чи нулем)
- Сформулювати властивості числових нерівностей.
- Дії з нерівностями.
- Числові проміжки (інтервали, відрізки, півінтервал).
- Що значить розв’язати нерівність? Розв’язок нерівності.
- Які нерівності називаються рівносильними?
- Сформулювати властивості нерівностей, які використовують при розв’язуванні нерівностей.
- Розв’язок системи. Що означає розв’язати систему?
-
Означення модуля: формула

Геометричний зміст модуля числа – відстань від початку відліку до точки, координатою якої є дане число. - Записати на дошці три класичні нерівності:
-
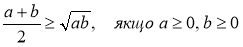 – (середнє арифметичне не перевищує середнє геометричне).
– (середнє арифметичне не перевищує середнє геометричне).
-
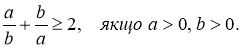
-
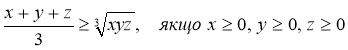 – нерівність Коші.
– нерівність Коші.
Учитель: Для того, щоб ви поглибили своє розуміння змісту цих нерівностей учениця підготувала повідомлення з історії математики.
Учениця розповідає:
Порівнювати яке з двох чисел більше, а яке менше, люди вміли багато тисячоліть тому. В «Началах» Евкліда доведено нерівність, яку прийнято записувати ![]() . Тільки тоді під a і b розуміли не довільні додатні числа, а довжини відрізків; доведення чисто геометричне і без знаків нерівності.
. Тільки тоді під a і b розуміли не довільні додатні числа, а довжини відрізків; доведення чисто геометричне і без знаків нерівності.
Знаки < і > вперше запровадив англійський математик Т. Гарріот в 1631 році, знаки ![]() і
і ![]() введено в XVIII ст.
введено в XVIII ст.
Нерівність 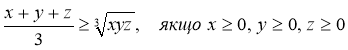 носить назву у математиці нерівність Коші для трьох доданків. Коші довів справедливість нерівності для будь-якої кількості доданків. Коші – французький математик. Роки життя (1789-1854) і багато написав наукових праць, які використовують в багатьох галузях науки і техніки.
носить назву у математиці нерівність Коші для трьох доданків. Коші довів справедливість нерівності для будь-якої кількості доданків. Коші – французький математик. Роки життя (1789-1854) і багато написав наукових праць, які використовують в багатьох галузях науки і техніки.
Ми з вами теж є винахідниками, продовжувачами математичних ідей. Зараз запропоновано буде двом учням знайти розв'язок задач.
-
Довести, що число
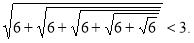
Підносимо ліву і праву нерівності до квадрата 5 разів. Дістанемо нерівність 6<9 (скористалися числовою нерівністю: якщо a>b, то a![]() >b
>b![]() ).
).
- Дати оцінку периметру рівностороннього трикутника із стороною а (в мм), де 54,2<a<54,3.
Розв'язування:
Периметр рівностороннього трикутника із стороною a обчислимо за формулою P= 3a. Помножимо кожну частину подвійної нерівності на 3.
162,6 < 3а < 162,9.
Учитель: Для того, щоб ви відчули впевненіть в своїх силах, ми застосуємо повторений матеріал для усних вправ.
Усні вправи
-
Довести нерівність
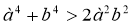 .
.
![]() , а цей вираз невід’ємний при будь-яких значеннях а і b.
, а цей вираз невід’ємний при будь-яких значеннях а і b.
- При яких значеннях змінної має зміст вираз:
а) ![]() ; б)
; б)![]()
Функція ![]() визначена тільки для
визначена тільки для ![]() , тому:
, тому:
а) ![]() ; б)
; б)![]() ;
;
![]()
![]() ;
;
х![]() 2;
2; ![]() .
.
[2;![]() ).
).
- Розв’язати нерівність:
1) | 2x – 1| > -1; 2) | 2x+6| ![]() -2; 3) |2x - 4|<5;
-2; 3) |2x - 4|<5;
x є ![]() . x є
. x є ![]() . -5 < 2x – 4 < 5;
. -5 < 2x – 4 < 5;
-1 < 2x < 9;
-0,5 < x < 4,5;
x є (-0,5; 4,5).
-
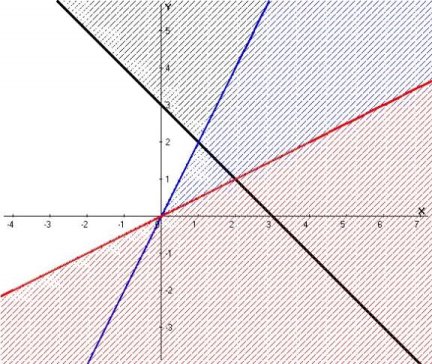 Поясніть, що зображено на малюнку:
Поясніть, що зображено на малюнку:
![]()
![]()
![]()
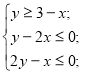
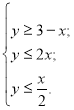
![]()
![]() На малюнку зображено множину розв`язків системи лінійних нерівностей з двома змінними.
На малюнку зображено множину розв`язків системи лінійних нерівностей з двома змінними.
![]() Побудовано графіки
Побудовано графіки
y = 3 – x; y = 2x, y = ![]() і заштриховані області, точки з яких задовольняють дані нерівності. Показано спільну частину – кут BDC, яка і є розв`язком системи нерівностей.
і заштриховані області, точки з яких задовольняють дані нерівності. Показано спільну частину – кут BDC, яка і є розв`язком системи нерівностей.
Вчитель: Це є приклад геометричної інтерпретації алгебраїчних задач, тобто відповідності між алгебраїчними співвідношеннями, в даному випадку нерівностей з одного боку і геометричними образами і прямими лініями з другого боку.
- Розв’язати нерівність з параметром:
(m - 1)x > 7m.
m = 1, то х∙0 < 7, х – будь-яке число;
m > 1, то х < ![]() ;
;
m < 1, то х > ![]() .
.
А тепер послухаємо, як справилися зі своїми завданнями учні, що працювали індивідуально.
Кожному учню поставити одне питання і оголосити оцінку.
Зараз нам знову надається можливість перевірити знання з теми «Нерівності». На сьогоднішній урок підготувала учениця софізм «Додатне число менше 0», де використовуються властивості нерівностей.
Дано: ![]() (1)
(1)
-
Помножимо обидві частини нерівності (1) на
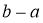 .
.
![]()
- Перетворимо даний вираз так, щоб у лівій частині був 0:
![]() ;
;
![]() . (2)
. (2)
Одержимо додатне число менше 0. Де тут допущена помилка? (Множили на від’ємне число і не змінили знак нерівності на протилежний).
-
Перевірка глибини осмислення учнями знань і ступеня їх узагальнення.
Вступне слово вчителя до письмових вправ
Підійшов час, коли ми будемо розв’язувати більш складні вправи, де ви повинні проявити вміння шукати різноманітні шляхи розв’язування цих питань, проявити свою творчість.
В зошитах запишемо число. Класна робота.
Тепер ми розв’яжемо вправи, де ви повинні показати свої вміння застосовувати знання при розв’язуванні складних вправ і показати вміння шукати шляхи розв’язання.
Розв’язати нерівність: |х-1|+|х+1|<4.
Бесіда
Вчитель: Якими способами ми на даний момент можемо розв’язати цю нерівність?
Учні: Трьома способами:
- Метод інтервалів.
- Графічний спосіб.
- Піднесенням до квадрату.
Ми розв’яжемо її методом інтервалів.
Викликати до дошки учня і розв’язувати нерівність:
- Шукаємо нулі підмодульних виразів: х1 = 1; x2 = -1.
-
Цими точками розбиваємо пряму на числові проміжки:

-
Розв’язуємо на кожному проміжку нерівність
-
( -
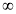 ; -1) - (х - 1) – (х + 1)
; -1) - (х - 1) – (х + 1)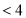 , -2x < 4, x > -2.
, -2x < 4, x > -2.
- (-1; 1) -(x -1) + (x + 1) < 4, -x + 1 +x + 1 < 4, 2 < 4,
-
( -
[-1; 1] – розв’язок.
-
(1; +
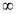 ) x – 1 + x + 1 < 4, 2x < 4, x < 2.
) x – 1 + x + 1 < 4, 2x < 4, x < 2.
(1; 2) – розв’язок.
Об’єднавши одержані результати, маємо: нерівність задовольняють всі значення змінної з інтервалу (-2; 2).
Учитель: Одержимо одразу домашнє завдання:
- Розв’язати графічним способом нерівність:
| x - 1| + |x + 1|<4
- Розв’язати графічно систему нерівностей:
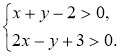
Повторити графічний спосіб.
На одержаних проміжках будуємо графіки.
y1 = | x - 1| + |x + 1| i y2=4.
![]()
![]()
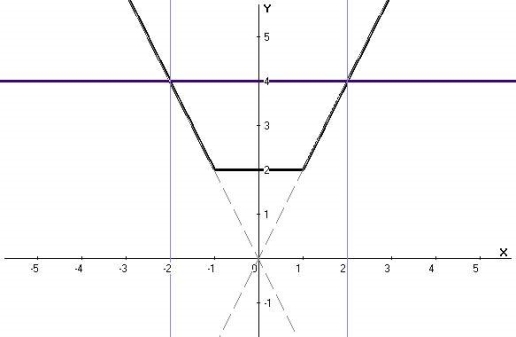
Знаходимо на числовій осі той проміжок, для якого точки графіка функції y1 = | x - 1| + |x + 1| нижче від відповідних точок прямої y2=4.
Далі розв’яжемо геометричну задачу. Зробимо це за допомогою властивості нерівності.
Задача. Всередині трикутника взято точку. Порівняти суму відстаней від цієї точки до вершин трикутника з його периметром. Або довести, що сума відстаней від будь-якої точки всередині трикутника до його вершин менша периметра трикутника.
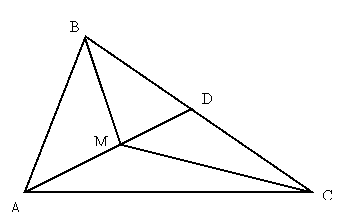 Продовжимо АМ до перетину з ВС в т. D. Із нерівності. трикутника випливає, що АВ+ВD>АD.
Продовжимо АМ до перетину з ВС в т. D. Із нерівності. трикутника випливає, що АВ+ВD>АD.
До обох частин нерівності додамо DС:
AB + (BD + DC) > AD + DC, або AB + BC > AD + DC. Розглянемо ∆ADC:
AD + DC > AM + MC. З нерівності трикутника випливає, що AB+BC > AM+MC. Анологічно AB + AC > BM + MC і BC + AC > AM + MB. Додаємо останні 3 нерівності, одержимо:
2(AB + BC + AC) >2(MA + MB + MC) або MA+MB+MC < P∆ABC.
Розглянемо нерівність з параметром
![]()
![]()
Як ми говорили, це по суті стислий запис множини нерівностей, які можна дістати з нерівності даної при різних конкретних значеннях параметра m.
Учень біля дошки розв’язує з коментуванням.
![]()
![]() : D: m
: D: m![]()
-
Якщо
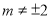 , то розв’язків немає.
, то розв’язків немає.
-
Якщо
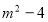
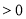 ,
, 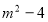 ,
, 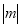
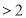
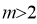 або
або 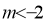 ,
, 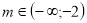
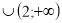 , то
, то 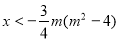 .
.
-
Якщо
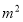
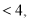
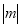
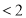 ,
, 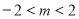 ,
, 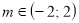 , то
, то 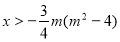 .
.
Відповідь підкреслити, щоб не переписувати.
На екрані розміщені різнорівневі завдання. Кожен учень обирає собі за бажанням завдання певного рівня.
Середній рівень
Довести нерівність ![]()
Розв’язування: ![]()
![]()
Достатній рівень
Застосувати метод інтервалів: ![]()
Розв’язування:
- Спочатку перенесемо 1 в ліву частину:
![]()
![]()
![]()
![]()
-
D(f):
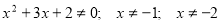 . Корені знайшли за допомогою теореми Вієта.
. Корені знайшли за допомогою теореми Вієта.
-
Нулі функції:
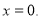

-
(-
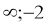 ) або (-1;0].
) або (-1;0].
Задати додаткове питання:
Якого вченого називали батьком алгебри? (Ф. Вієта (1540-1603 р.) французького вченого.)
Високий рівень
Розв’язати нерівність: ![]()
![]()
![]()
![]()
![]()
Спрощений результат: 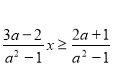 , D(f): a
, D(f): a![]() .
.
-
якщо
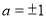 , то коренів не існує;
, то коренів не існує;
-
якщо
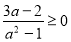 , то
, то 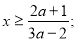

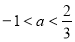 і
і 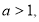 то
то 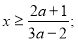
-
якщо
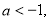
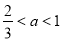 , то
, то 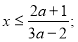
-
якщо
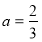 , то
, то 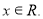
Підсумок уроку
Сьогодні на уроці ми повторили і систематизували знання з теми «Нерівності». Розглянули питання лінійної нерівності з однією змінною, лінійної нерівності, яка містить змінну під знаком модуля, лінійної нерівності з параметром, графічне розв’язування систем лінійних нерівностей з двома змінними, метод інтервалів для розв’язування нерівностей. Розв’язали ряд вправ, де показали свої вміння застосовувати властивості, означення, певні алгоритми в стандартних умовах і більш складних ситуаціях і побачили важливість вивченої теми.
Домашнє завдання:
- Довести нерівність:
![]()
Доведення: за нерівністю Коші:
![]() (1)
(1)
![]() (2)
(2)
Перемножуємо (1) на (2) дістанемо:
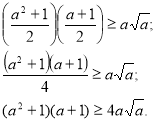
Література
- В. П. Коваленко, В. Я. Кривошеєв, Л. Я. Лемберський. Алгебра: експерим. навч. посібник для 8 кл. шк.. з поглибленим вивченням математики і спец. шк.. фізико-мат. профілю. – К.: Освіта, 1995. – 303 с.
- Апостолова Г. В. Я сам! Навчальний посібник з алгебри ля тих, хто у сьомому класі та старше, з опорними схемами та порадами. – К.: Факт, 1997. – 204 с. – укр.. мовою.
- Апостолова Г. В., Ясінський В. В. Перші зустрічі з параметром (видання друге) – К.: Факт, 2006.


про публікацію авторської розробки
Додати розробку

