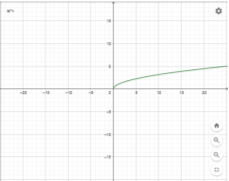
ФУНКЦІЯ y=√x, ЇЇ ГРАФІК І ВЛАСТИВОСТІ
Алгебра, 8 клас
Урок № __
Тема. ФУНКЦІЯ 
, ЇЇ ГРАФІК І ВЛАСТИВОСТІ
Мета уроку:
-
формування предметних компетентностей: сформувати вміння будувати графік функції
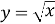, домогтися засвоєння учнями основних властивостей цієї функції, сформувати вміння застосовувати властивості функції 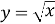до розв’язування задач;
- формування ключових компетентностей: формувати вміння робити висновки на основі інформації, поданої у вигляді графіка; формувати розуміння важливості чітких та лаконічних формувань; формувати вміння аргументувати, доводити правильність тверджень, ухвалювати оптимальні рішення; сприяти самовихованню відповідальності за результати своєї роботи.
Очікувані результати: учні повинні вміти будувати графік функції , характеризувати властивості цієї функції, застосовувати їх до розв’язування задач.
Ключові поняття: функція, функціональна залежність, графік функції, властивості функції, незалежна змінна, залежна змінна, зростання функції, графічний спосіб розв’язування рівняння.
Тип уроку: засвоєння нових знань і вмінь.
Обладнання та наочність: підручник для 8 класу з алгебри (авт.О.С.Істер, 2016р.), картки завдань, матеріали для мультимедійного супроводу уроку, інтерактивні вправи (для проведення усного рахунку та бліц-опитування), ноутбук, інтерактивна дошка (або телевізор), доступ до інтернету.
ПЕРЕБІГ УРОКУ:
- Організаційний етап
- Привітання, перевірка готовності та налаштування учнів до роботи на уроці.
- Усний рахунок (інтерактивна вправа).
- Перевірка домашнього завдання
- Вибірковий контроль.
Учитель вибірково перевіряє зошити, відповідає на запитання учнів.
- Фронтальна робота з класом.
Вправа «Знайди помилку» (На дошку проектуються виконані з помилками розв’язання вправ з домашнього завдання, а учні повинні перевірити їх на правильність та вказати допущені помилки з обгрунтуванням).
- Індивідуальна робота.
Бліц-опитування (дані завдання пропонуються кільком учням до виконання)
Вчитель підсумовує роботу учнів класу на даному етапі.
- Актуалізація опорних знань
- Формування теми, мети й завдань уроку; мотивація навчальної діяльності
|
Актуальна задача |
Компанія займається вирощуванням та реалізацією саджанців паркових троянд. Дослідження ринку показали, що кількість n саджанців. Проданих протягом тижня, залежить від тривалості t щоденного рекламного ролика (у с), що транслювався впродовж цього тижня. Причому ця залежність виражається формулою 1) якою є залежність t від n; 2) скільки часу має тривати щоденний рекламний ролик, щоб обсяг продажу становив 900 саджанців. |
|
Розв’язання:
1) Якщо
2) За умовою кількість саджанців має складати 900 штук, тому шуканий час |
|
Якби в задачі було задано залежність 
і за відомою тривалістю рекламного ролика потрібно було б знайти кількість проданих саджанців, то можна було б отримане рівняння розв’язати, наприклад, графічним способом. А для цього потрібно знати, як виглядає графік функції .
- Сприйняття й усвідомлення нового матеріалу
- План викладення нового матеріалу
-
Побудова графіка функції .
-
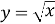Властивості функції .
-
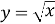Застосування властивостей функції 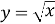до розв’язування задач.
-
Фронтальна бесіда (Порівняння ірраціональних чисел за допомогою графіка функції ).
|
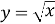Властивість функції |
Властивість |
Обгрунтування |
|
Графік проходить через початок координат. |
При х=0 маємо у(0)= |
|
|
Незалежна змінна набуває лише невід’ємних значень. |
За означенням арифметичного квадратного кореня підкореневий вираз може бути лише невід’ємним, тобть х |
|
|
Залежна змінна набуває лише невід’ємних значень. |
За означенням арифметичного квадратного кореня значення кореня може бути лише невід’ємним, тобто у |
|
|
Графік розміщений лише в І координатній чверті. |
х |
|
|
Якщо значення x більшується, то значення y збільшується, тобто функція зростає при всіх |
Читаємо графік зліва направо
|
- Колективне усних вправ: № 702, 704.
Порівняйте за допомогою графіка функції числа 
, 
та знайдіть усі цілі числа, розташовані між ними на числовій прямій.
Розв’язання:
|
Крок |
Зміст дії |
Результат дії |
|
1 |
Знайдемо на графіку функції точку, що відповідає абсцисі |
|
|
2 |
Знайдемо на графіку функції точку, що відповідає абсцисі |
|
|
3 |
Порівняємо |
|
|
4 |
З’ясуємо за графіком, що між числами
Маємо: |
|
|
Зверніть увагу! Якщо в умові завдання йдеться про розташування числа на числовій прямій, у ході розв’язування можна розглядати будь-яку высь – або Ох, або Оу. |
||
Відповідь:
;цілі числа 2 і 3.
|
ВАЖЛИВО ЗНАТИ
|
Якщо |
- Колективне виконання завдань під керівництвом учителя: № 706 (1,2), № 708 (1)
- Робота в групах. Виконання завдань: № 706 (3,4), № 708 (2).
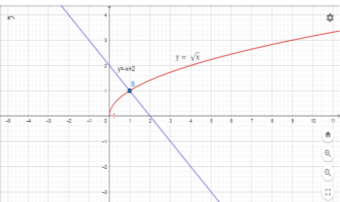
- Фронтальна бесіда (Розв’язування рівнянь графічним способом).
Розв’яжіть рівняння 
графічним способом.
Розв’язання:
|
Крок |
Зміст дії |
Результат дії |
|
1 |
Запишемо рівняння у вигляді |
|
|
2 |
Побудуємо в одній системі координат графіки функцій |
Перевірка:
|
|
3 |
Визначимо точку В перетину графіків функцій і знайдемо її абсцису |
|
|
4 |
Для того щоб перевірити, чи є знайдене число 1 точним коренем або наближеним значенням, підставимо його у задане рівняння. Робимо висновок |
- Колективне виконання завдань під керівництвом учителя: № 711.
- Робота в групах. Виконання завдань: № 712.
- Осмислення нового матеріалу
Колективне виконання завдань під керівництвом учителя: № 713.
- Підведення підсумків уроку
- Самооцінювання учнів.
На координатному промені, на який нанесено шкалу з поділками від 10 до 100 з кроком 10 одиниць, поставте позначку, на тій поділці, яка відповідає ступеню опанування вами нового матеріалу, відповідь обгрунтуйте.
- Оцінка діяльності учнів на уроці, обгрунтування.
- Домашнє завдання
-
Опрацювання теоретичного матеріалу за підручником
.
-
Знати відповіді на запитання після ст.158.
- Повторити формули скороченого множення; розкладання многочленів на множники, властивості кореня квадратного.
-
Виконати завдання за підручником: завдання для перевірки знань до
(ст.162-163)
1
про публікацію авторської розробки
Додати розробку