Дроби. Дробові вирази. Раціональні вирази. Допустимі значення змінних
Тема. Дроби. Дробові вирази. Раціональні вирази. Допустимі значення змінних
Мета: домогтися засвоєння учнями термінології, вивченої на попередньому уроці, та засвоєння змісту алгоритму знаходження значень змінної, при яких даний раціональний дріб дорівнює нулю; сформувати вміння застосовувати вивчений алгоритм для розв'язування вправ, що передбачають знаходження значень змінних, при яких значення поданого раціонального дробу дорівнює нулю; вдосконалити вміння, формування яких було розпочато на попередньому уроці.
Тип уроку: застосування знань та вмінь.
Наочність та обладнання: опорний конспект «Дробові вирази. Раціональні вирази».
Хід уроку
I. Організаційний етап
Перевірка готовності учнів до уроку, налаштування на роботу.
II. Перевірка домашнього завдання
- Виконання вправ домашньої роботи перевіряється ретельно в учнів, які потребують додаткової педагогічної уваги (зібрати зошити на перевірку).
- Математичний диктант
Варіант 1
-
Запишіть вирази:
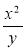 ; (х – у); (2х + у) : (2х + у);
; (х – у); (2х + у) : (2х + у); 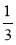 ху(х + у).
ху(х + у).
Підкресліть цілі вирази.
-
Чи можна подати вираз
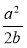 у вигляді многочлена?
у вигляді многочлена?
-
Які значення змінної допустимі для виразу
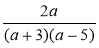 ?
?
- Які значення змінної допустимі для виразу (а + 3)(а – 5)?
5*. Запишіть раціональний дріб, ОДЗ якого є всі числа, крім 0 і -5.
Варіант 2
-
Запишіть вирази:
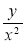 ; (x + y) : (x + y); (x – 2y)(x + 2у);
; (x + y) : (x + y); (x – 2y)(x + 2у);  х(х – у).
х(х – у).
Підкресліть цілі вирази.
-
Чи можна подати вираз
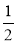 ab(x + у) у вигляді многочлена?
ab(x + у) у вигляді многочлена?
- Які значення змінної допустимі для виразу (х – 5)(х + 7)?
-
Які значення змінної допустимі для виразу
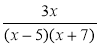 ?
?
5*. Запишіть раціональний дріб, ОДЗ якого є всі числа, крім —2 і 2.
III. Формулювання мсти і завдань уроку
Створенню відповідної мотивації на уроці може сприяти виконання учнями завдання:
-
Знайдіть значення виразів
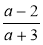 ,
, 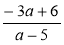 ,
, 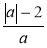 при а = 2. Порівняйте здобуті результати. Що ви помітили?
при а = 2. Порівняйте здобуті результати. Що ви помітили?
- Чи існують інші значення змінної а, при яких ці вирази дорівнюють нулю?
-
Чи буде дорівнювати нулю при а = -2 значення виразу
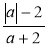 ? Чому?
? Чому?
Після обговорення результатів, здобутих у ході виконання запропонованих вище завдань спільними зусиллями доходимо висновку: одним із важливих питань, що пов'язані з поняттям дробового виразу, є питання про умови рівності дробу нулю. Вивчення цього питання і є основною дидактичною метою уроку. Завдання на урок логічно випливають із цієї мети: сформулювати загальне правило, а також навчитися застосовувати це правило під час розв'язування задач.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями змісту навчального матеріалу уроку слід поновити в пам'яті учнів зміст таких понять та алгоритмів: виконання арифметичних дій зі звичайними дробами, перетворення цілих виразів (одночленів, многочленів) у многочлен і розкладання цілих виразів на множники, способи розв'язання цілих рівнянь, що зводяться до лінійних.
Виконання усних вправ
- Назвіть чисельник і знаменник раціонального дробу:
а) ![]() ; б)
; б) ![]() ; в)
; в) 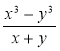 ; г)
; г) ![]() .
.
-
Розв'яжіть рівняння: а) -2х = 4; б) х + 5 = 0; в) у2 = 0; г)
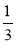 у = 3; д) 0,5х = 5; є) х2 = -1.
у = 3; д) 0,5х = 5; є) х2 = -1.
- Подайте вираз у вигляді добутку:
а) 10х + 15у; б) а2 – 25; в) 42у2 – 21у; г) 48с – 8с2; д) 6т – 24; є) 16x – xy;
ж) 27 + х3; з) а8 – а7.
- Обчисліть:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д) 2,3 · 3; є) 8,6 : 2; ж) 15 : 2;
; д) 2,3 · 3; є) 8,6 : 2; ж) 15 : 2;
з) 2,1 : 2; и) 6 : 0,3; к) 19 : 3; л) ![]() : 0,3.
: 0,3.
V. Застосування знань
План вивчення нового матеріалу
- Умова рівності дробу нулю.
- Алгоритм застосування умови рівності дробу нулю.
- Приклади розв'язання завдань на застосування вивченого алгоритму.
Умова рівності дробу нулю є одним із питань, які передбачені програмою з математики і мають широке практичне застосування, тому вже під час першого знайомства з поняттям раціонального дробу слід приділити йому належну увагу.
Виходячи з результатів обговорення питань, запропонованих на етапі мотивації навчальної діяльності учнів, спочатку вчитель формулює умову рівності дробу нулю (див. опорний конспект №1) у вигляді системи, що складається з двох умов: знаменник дробу не дорівнює нулю, чисельник дорівнює нулю.
Після чого складається орієнтовна схема дій для розв'язування задачі на знаходження значень змінних, при яких раціональний дріб дорівнює нулю:
1) знайти ОДЗ раціонального дробу;
2) знайти значення змінної, при яких чисельник дробу дорівнює нулю (прирівняти чисельник дробу до нуля та розв'язати здобуте рівняння);
3) з'ясувати, які корені рівняння (див. попередній пункт) не входять до ОДЗ;
4) записати відповідь — корені рівняння (див. 2 пункт), які входять (не суперечать) ОДЗ.
Після формування алгоритму необхідно проілюструвати застосування алгоритму на різних прикладах: без наявності сторонніх коренів та за наявності сторонніх коренів.
VI. Засвоєння вмінь
Виконання усних вправ
-
Який із записів є умовою, якщо дріб
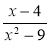 дорівнює нулю?
дорівнює нулю?
а) х – 4 ≠ 0; б) х2 – 9 ≠ 0; в) 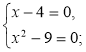 г)
г) 
- Складіть дріб, для якого умова рівності нулю записується так:
а) 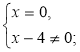 б)
б) 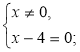 в)
в) 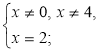 г) х = 3.
г) х = 3.
Виконання письмових вправ
3 метою реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту:
- Знаходження значень змінних, при яких значення раціонального дробу дорівнює деякому числу або нулю.
1) При якому значенні змінної значення дробу ![]() дорівнює:
дорівнює:
а) 1; б) 0; в) -1; г) 3?
2) При яких значеннях змінної значення наведених дробів дорівнюють нулю?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
- Знаходження ОДЗ (дробового) раціонального виразу.
1) Знайдіть допустимі значення змінної у виразі:
а) 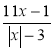 ; б)
; б) 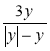 ; в)
; в) 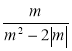 ; г)
; г) 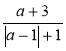 .
.
2) Укажіть допустимі значення змінної у виразі:
а) х2 – 8х + 9; б) ![]() ; в)
; в) ![]() ; г)
; г) 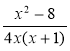 ; д)
; д) ![]() ;
;
є) ![]() .
.
3) Знайдіть область визначення функції:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
- Знаходження значень дробового виразу при даних значеннях змінної (змінних).
Знайдіть значення виразу 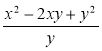 при:
при:
а) х = 44, у = 4; б) х = 46, у = 46; в) х = 1,25, у = 0,25.
- Складання виразу за текстовою умовою та обчислення значення складеного виразу при заданих значеннях змінних.
1) Складіть вираз для розв'язання задачі.
Катер проплив 25 км за течією річки і 20 км проти течії. Знайдіть час руху катера, якщо його швидкість у стоячій воді v км/год, а швидкість течії річки и км/год.
2) Складіть вираз для розв'язання задачі.
Потяг за певний час повинен був подолати шлях 250 км, рухаючись зі швидкістю а км/год. Але через 2 год його було затримано. Тому, щоб прибути до місця призначення вчасно, він збільшив швидкість на 25 км/год. Знайдіть тривалість затримки.
- Виконання вправ на перетворення цілих виразів із застосуванням алгоритмів, вивчених у 7 класі.
Розкладіть на множники:
а) a2b + ab2; б) х3у – ху3; в) 7х2 – 14ху + 21ах; г) 9ху – 3bу + 15ау;
д) х4 – х3 + х2 – х; є) с4 – 2с3 – с2 + 2с; ж) (а – 2)2 – 25а2;
з) (b + 3)2 – 36b2; и) 125x3 + 8; к) 216х3 – 27; л) (а + 1)3 + а3;
м) (b + 2)3 – 863.
- Для учнів, які мають достатній та високий рівень знань — виконання логічних вправ та завдання підвищеного рівня складності.
1) Складіть дріб, що містить змінну х у знаменнику і має зміст при всіх значеннях х.
2) Доведіть тотожність:
а) а4 + а2 + 1 = (а2 + а + 1)(а2 – а + 1);
б) b8 + b4 + 1 = (b4 + b2 + 1)(b4 – b2 + 1);
в) с4 + 4 = (с2 – 2с + 2)(с2 + 2с + 2).
3) Знайдіть пропущений вираз:
|
28 |
a2 – (b – с)2 |
|
2 · 2 · 7 |
7 |
VII. Підсумки уроку
Серед запропонованих чисел виберіть ті, що задовольняють умову для дробу:
а) дріб ![]() існує;
існує;
б) дріб ![]() дорівнює нулю.
дорівнює нулю.
Числа: 4; -4; 16; -16.
VIII. Домашнє завдання
- Вивчити зміст умови, коли дріб дорівнює нулю, повторити означення раціонального дробу, ОДЗ виразу.
- Виконати вправи на закріплення алгоритму знаходження значень змінних, при яких дріб дорівнює нулю та повторення алгоритму знаходження ОДЗ виразу.
- На повторення: повторити скорочення звичайних дробів та розкладання многочленів на множники, ділення степенів з натуральним показником.


про публікацію авторської розробки
Додати розробку
