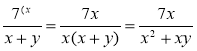Основна властивість дробу. Скорочення дробів
Тема. Основна властивість дробу. Скорочення дробів
Мета: домогтися засвоєння учнями змісту основної властивості раціонального дробу, понять скорочення дробу та правила знаків; сформувати вміння відтворювати зміст названих понять та використовувати вивчені поняття для розв'язування вправ на скорочення раціональних дробів та перетворення їх за допомогою правила знаків.
Тип уроку: засвоєння знань та вмінь.
Наочність та обладнання: опорний конспект «Основна властивість дробу».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Тестова робота № 1
Варіант 1
- Який із наведених виразів є раціональним дробом?
|
A |
Б |
В |
Г |
|
2a – b |
ab |
|
а2 + |
- Який із наведених виразів має зміст при будь-якому значенні змінної х?
|
А |
Б |
В |
Г |
|
|
|
|
х2 + 4 |
-
При якому значенні х дріб
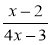 не існує?
не існує?
|
А |
Б |
В |
Г |
|
х = 2 |
х = |
х = |
х = |
-
При якому значенні х дріб
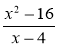 дорівнює нулю?
дорівнює нулю?
|
А |
Б |
В |
Г |
|
± 4 |
4 |
- 4 |
16 |
Варіант 2
- Який із наведених виразів є цілим виразом?
|
А |
Б |
В |
Г |
|
|
аb – 1 |
|
|
- Який із наведених виразів має зміст при будь-якому значенні змінних?
|
А |
Б |
В |
Г |
|
х2 + 3х |
|
|
|
-
При якому значенні х дріб
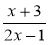 не існує?
не існує?
|
А |
Б |
В |
Г |
|
х = 2 |
х = |
х = -3 |
х = |
-
При якому значенні х дріб
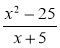 дорівнює нулю?
дорівнює нулю?
|
А |
Б |
В |
Г |
|
х = 5 |
х = -5 |
х = ±5 |
х = 25 |
III. Формулювання мети і завдань уроку
На цьому етапі уроку буде доречним слово вчителя про те, що звичайні і раціональні дроби мають однакову основну властивість і загальні правила виконання арифметичних дій. Зрозуміло, що роботу з вивчення дій над раціональними дробами слід розпочинати з основної властивості — саме її вивчення і представляє основну дидактичну мету уроку.
Завданнями на урок є: сформулювати алгоритми застосування основної властивості раціонального дробу на основі виконання дій із многочленами.
Як варіант роботи з дітьми, які мають високий рівень інтелектуальної діяльності, пропонуємо завдання.
Знайдіть значення виразів ![]() і
і ![]() при а = 4. Порівняйте здобуті результати. Порівняйте вирази. Що ви помітили?
при а = 4. Порівняйте здобуті результати. Порівняйте вирази. Що ви помітили?
Після обговорення результатів виконаної роботи з'являється гіпотеза про те, що значення раціональних дробів не зміниться під час виконання ділення або множення чисельника і знаменника дробу на один і той самий вираз, що не дорівнює нулю. Підтвердження цієї гіпотези і є основною метою уроку.
IV. Актуалізація опорних знань та вмінь
Для підготовки учнів до сприйняття нового матеріалу доцільно розв'язати усні вправи на повторення алгоритмів виконання арифметичних дій із раціональними числами, алгоритмів перетворень цілих виразів, вивчених у 7 класі (особливо різних способів розкладання многочленів на множники), а також матеріалу, вивченого на попередніх уроках у 8 класі (знаходження ОДЗ раціонального виразу).
Виконання усних вправ
-
Скоротіть дроби:
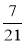 ;
; 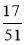 ;
; 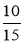 ;
; 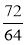 .
.
-
Зведіть дроби до знаменника 36;
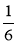 ;
; 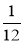 ;
; 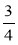 ;
; 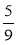 ;
; 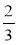 ;
; 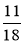 .
.
-
Обчисліть:
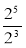 ;
; 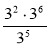 ;
; 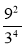 ;
; 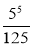 ;
; 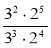 ;
; 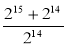 .
.
- Подайте вирази у вигляді добутку:
25 – у2; a2 + ab; 8 + х3; 1 + а2 - 2а; 3х6 – 12x2; b10 – b2.
- Подайте число 3 у вигляді дробу зі знаменником: 2; 5; 1; 4; 10.
- Серед виразів:
х + у; - х + у; - х – у; у – х; х – у; (х – у)2; (у – х)2; (- х – у)2; (х + у)2; (-х – у)3;
(х – у)2; -(х + у)3; - (х – у)3
знайдіть: а) тотожно рівні; б) протилежні. Доведіть.
V. Засвоєння знань
План вивчення нового матеріалу
- Уявлення про основну властивість звичайного дробу; її адаптація на раціональний дріб (із доведенням).
- Основна властивість дробу і скорочення дробів. Алгоритм скорочення раціонального дробу.
- Основна властивість дробу і правило знаків.
|
Конспект 2 |
|
Основна властивість дробу |
|
1. Якщо
|
|
Приклад. Скоротити дріб |
|
Розв'язання |
|
1) Розкладемо чисельник і знаменник дробу на множники: |
|
2) Поділимо чисельник і знаменник здобутого дробу на спільний множник (а + 3); маємо:
Отже: |
|
2. Якщо
|
|
Приклад. Скоротити дріб |
|
1) Розкладемо чисельник і знаменник раціонального дробу на множники:
|
|
2) Помітивши, що (3 – с) і (с – 3) — протилежні вирази, скористаємось правилом знаків: поміняємо, знак перед дробом, і наприклад, знак множника
(3 – с) у чисельнику: |
|
3) Скоротивши даний дріб на спільний множник чисельника і знаменника (с–3); маємо: |
|
Отже, |
|
3. Якщо
Приклад. Звести дріб |
|
Розв'язання |
|
1) Розкладемо новий знаменник на множники: х(х + у). 2) Знайдемо додатковий множник; для цього новий знаменник поділимо на знаменник даного дробу.
3) Помножимо чисельник і знаменник даного дробу на х (додатковий множник): |
Викладення навчального матеріалу уроку слід розпочати із формулювання і доведення основної властивості раціонального дробу, яка подається як у математичному (![]() ,
,![]() , де А, В, С — деякі многочлени, причому В ≠ 0, С ≠ 0), так і в словесному вигляді.
, де А, В, С — деякі многочлени, причому В ≠ 0, С ≠ 0), так і в словесному вигляді.
Доведення властивості спирається на уявлення про дріб як запис частки від ділення двох виразів та на залежність між компонентами дії ділення.
Після формування в учнів уявлення про «дві сторони» основної властивості раціонального дробу подається назва одного з перетворень, що входять до основної властивості дробу, — скорочення дробів; при цьому наголошується на тому, що під скороченням дробів розуміють ділення чисельника і знаменника раціонального дробу на спільний множник чисельника і знаменника, тому скорочення раціональних дробів передбачає виконання певних дій у певній послідовності для виділення цього спільного множника. Складається алгоритм скорочення раціональна дробів.
Під час розв'язування прикладів на застосування складеного алгоритму скорочення дробів можна запропонувати вправи, що підготують учнів до сприйняття правила знаків для раціональних дробів (або до самостійного складання цього правила в разі високого рівня підготовки учнів до самостійної інтелектуальної діяльності). Після формулювання загального правила розглядаються приклади, під час розв'язування яких необхідно використати правило знаків, та коментуються загальні способи дій у разі застосування цього правила (якщо на опрацювання правила знаків не вистачить часу на уроці № 3, можна розглянути його на уроці № 4 разом із питанням про зведення дробу до нового знаменника).
VI. Засвоєння вмінь
Виконання усних вправ
-
Які з дробів
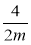 ,
, 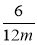 ,
, 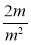 тотожно рівні дробу
тотожно рівні дробу 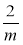 ?
?
- Назвіть спільний множник чисельника і знаменника дробу та скоротіть дроби:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
- Чи правильні рівності:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ?
?
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту:
- Скорочення раціонального дробу.
1.1. На одночлен.
1) Виділіть спільний множник чисельника та знаменника дробу й скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) 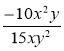 .
.
2) Скоротіть дріб: а) 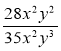 ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
1.2. На многочлен (який уже виділено в чисельнику і знаменнику поданих раціональних дробів).
1) Скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2) Скоротіть дріб: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
- Скорочення раціонального дробу з попереднім розкладанням чисельника і знаменника на множники.
1) Розкладіть на множники чисельник і знаменник і скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 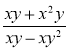 .
.
2) Скоротіть дріб: а) ![]() ; б)
; б) ![]() ; в)
; в) 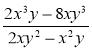 .
.
3) Розкладіть на множники чисельник і знаменник і скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) 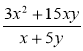 .
.
4) Скоротіть дріб: а) 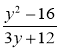 ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) 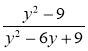 .
.
- Виконання вправ на використання правила знаків перед скороченням дробів.
1) Спростіть вираз:
а) ![]() ; б)
; б) 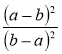 ; в)
; в) 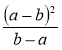 ; г)
; г) 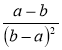 ; д)
; д) 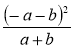 ; є)
; є) 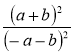 .
.
2) Скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() ; ж)
; ж) ![]() ; з)
; з) 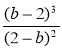 .
.
- Знаходження значень раціональних дробів із попереднім їх скороченням.
1) Знайдіть значення виразу:
а) ![]() при а = 48, b = 16; а = -4,2, b = 11;
при а = 48, b = 16; а = -4,2, b = 11;
б) 15x2y3 : (30xy2) при х = 300, у = 0,06.
2) Знайдіть значення виразу ![]() при а = 4; а =
при а = 4; а = ![]() .
.
- Виконання вправ на повторення: вправи на знаходження ОДЗ дробів і умови рівності дробу нулю.
1) Знайдіть допустимі значення змінної у виразі:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
2) Складіть дріб зі змінною х, яка має зміст при всіх значеннях змінної, крім:
а) х = 2; б) х = 0 і х = 3; в) х = -3 і х = 3; г) х = ![]() і х =
і х = ![]() .
.
- Виконання логічних вправ та завдань підвищеного рівня складності для учнів, які мають достатній та високий рівень знань.
1) Скоротіть дріб:
а) ![]() ; б)
; б) 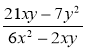 ; в)
; в) 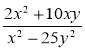 ; г)
; г) 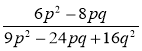 ;
;
д) ![]() ; є)
; є) ![]() ; ж)
; ж) ![]() ;
;
з) 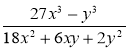 .
.
2) Знайдіть пропущений вираз:
|
|
а ≠ 0 |
а2 + 1 |
|
|
1 |
9 |
VII. Підсумок уроку
Яка рівність є записом правильно виконаного скорочення раціональних дробів?
а) 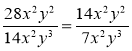 ; б)
; б) 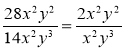 ; в)
; в) 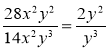 ; г)
; г) 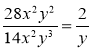 .
.
VIII. Домашнє завдання
- Вивчити зміст основної властивості дробу та алгоритму ГГ застосування для скорочення раціональних дробів.
- Розв'язати вправи на скорочення дробів (рівня, що відповідає вправам класної роботи).
- На повторення: знаходження значень змінних, при яких дріб дорівнює нулю, та повторення алгоритму знаходження ОДЗ виразу.


про публікацію авторської розробки
Додати розробку