Геометрія 8 клас поглиблений рівень

Про матеріал

розробка уроку з геометрії для учнів 8 класу, поглиблений рівень вивчення математики , по темі "Коло 9 точок. Пряма Ейлера"

Перегляд файлу

Коло дев’яти точок. Пряма Ейлера

Актуалізація Коло дев’яти точок — це коло, яке можна побудувати для будь-якого трикутника. Так називається воно через те, що воно проходить через дев’ять важливих точок, шість з яких лежать на самому трикутнику (за винятком тупокутних трикутників). Ці точки:

-середина кожної сторони трикутника

-основа кожної висоти

-середини відрізків, що сполучають вершини трикутника з ортоцентром

Задача1

Дано коло з центром у точці О. Через точку С, що лежить поза колом, до кола проведено дотичну СВ (В – точка дотику). Січна СО перетинає коло в точці А. Кут ВАС дорівнює 30⁰. Знайти кути трикутника ВОС.

Розв'язання.

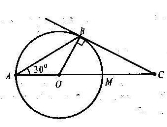1) (за властивістю рівнобедреного трикутника).

2) (за властивістю зовнішнього кута трикутника).

3) (за означенням дотичної).

4) (за властивістю гострих кутів прямокутного трикутника).

Задача2

Довести, що висоти АН₁, ВН₂, СН₃ гострокутного трикутника АВС поділяють навпіл кути трикутника Н₁Н₂Н₃.

Доведення.

Оскільки , то навколо чотирикутника АН₃НН₂ можна описати коло.

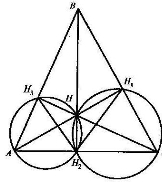Тоді як вписані, що спираються на одну дугу. Аналогічно доводимо, що .

Але , тому що вони доповнюють кут АВС до 90⁰. Звідси . Так само доводимо, що і .

Задача3

На медіані АМ трикутника АВС узято точку К так, що 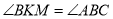. Довести, що .

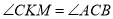Доведення.

Продовжимо медіану АМ на відстань, що дорівнює її довжині.

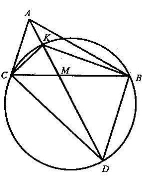
. Отже, точки С, К, В, Д лежать на одному колі. Тоді (як кути, що спираються на дугу СД), але . Звідси .

Задача 4

Довести, що квадрат бісектриси трикутника дорівнює різниці між добутком сторін, між якими вона проходить, і добутком відрізків третьої сторони, на які її поділяє бісектриса.

Доведення.

Навколо трикутника АВС опишемо коло і продовжимо бісектрису СД трикутника до перетину з колом у точці Е.

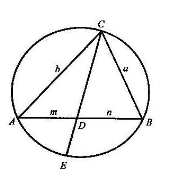Нехай ВС=а, АС=в, АD=т, ВD=п, СD=у, DЕ=х.