Графіки тригонометричних функцій та їх застосування

Графіки тригонометричних функцій та їх застосування Виконали: учні 10 класу Перещепинської ЗОШ I-III ст. №1 Анастасян Давид Мазан Владислав Томяк Анна

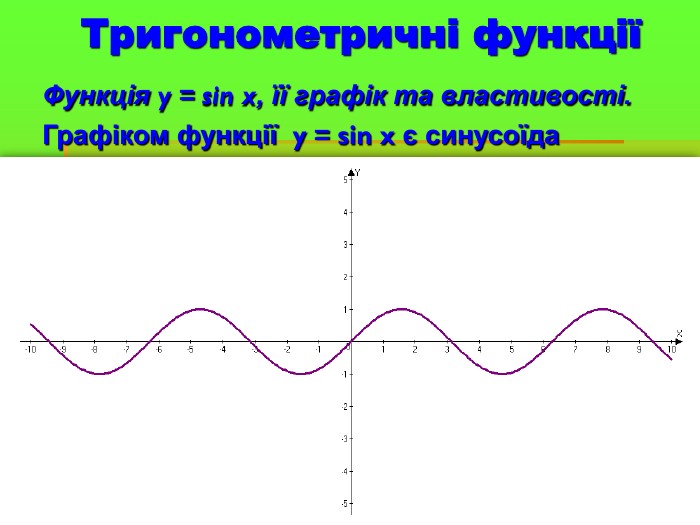
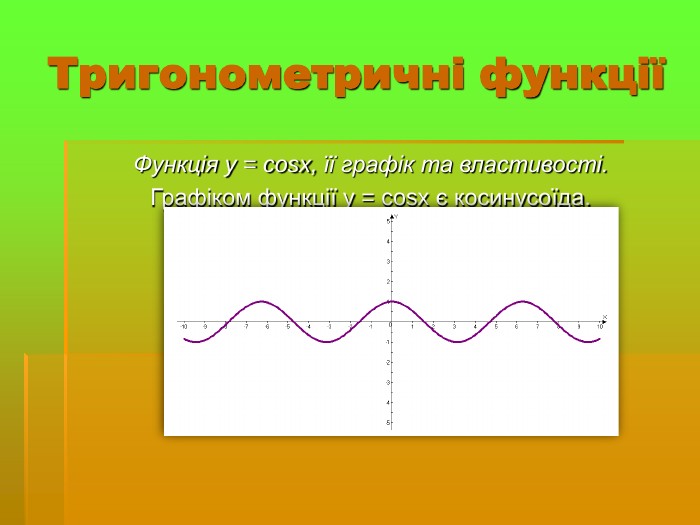
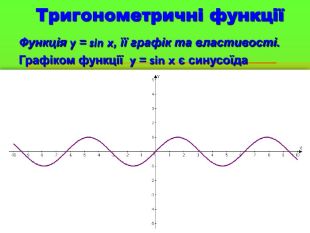
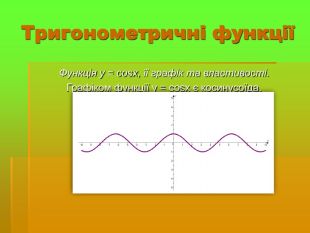
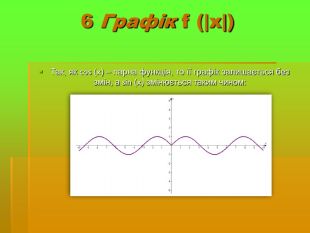
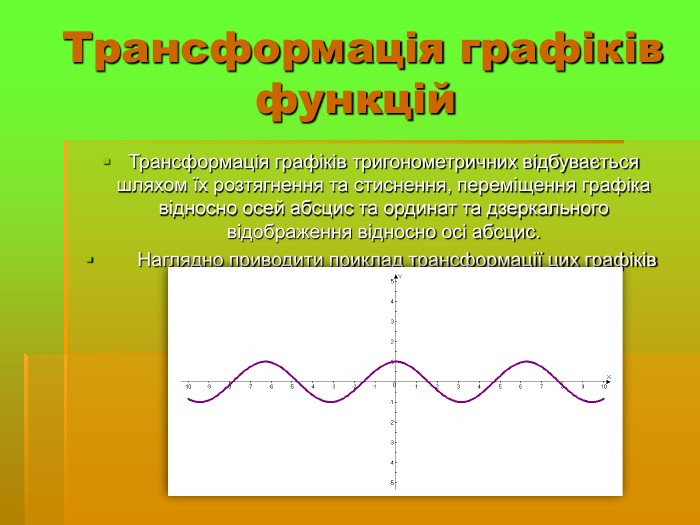
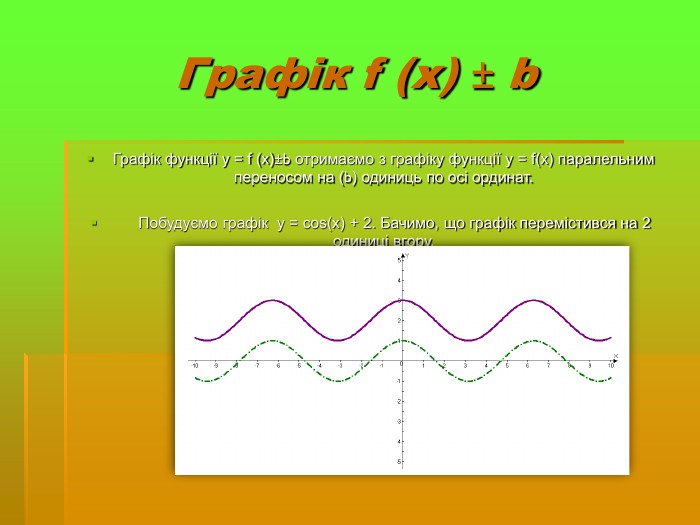
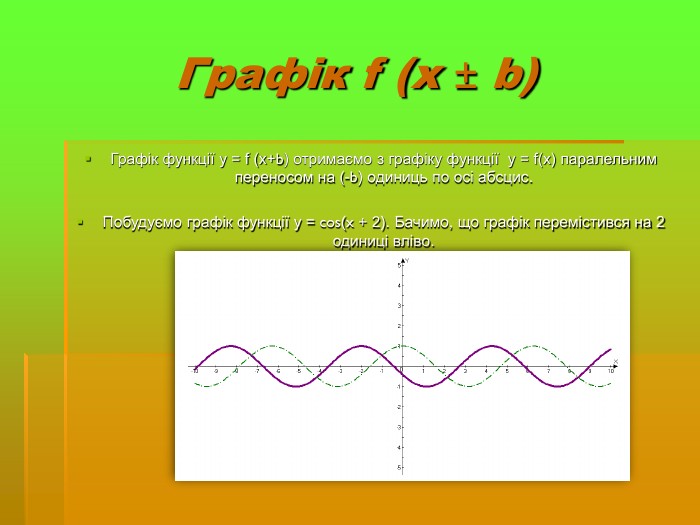
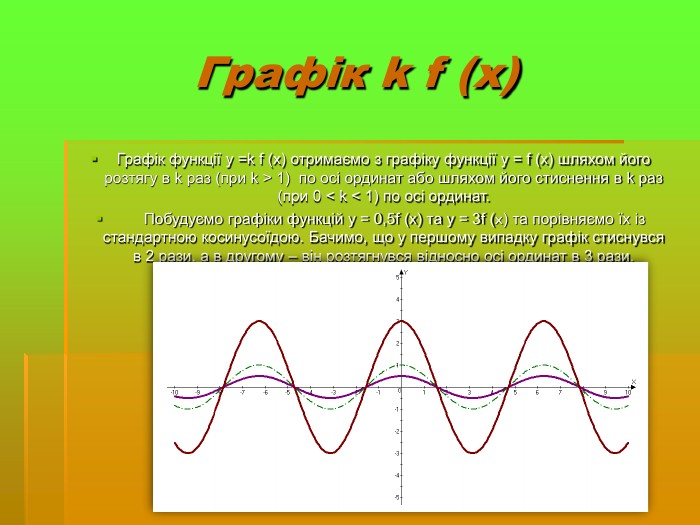
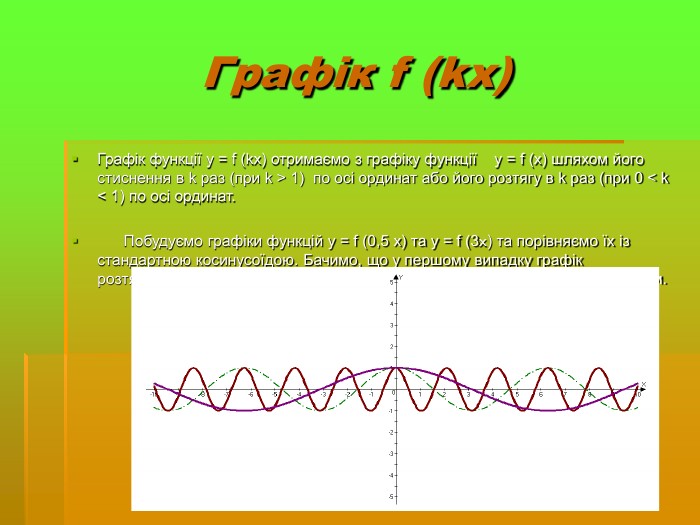
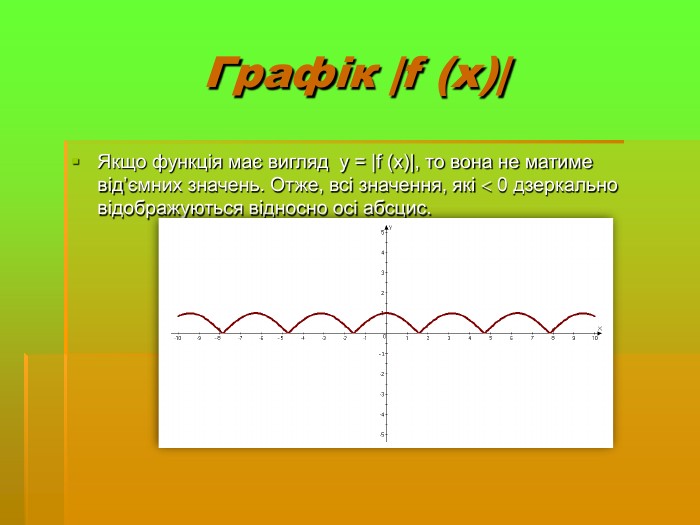
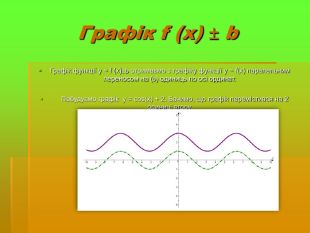
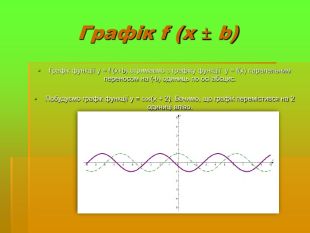
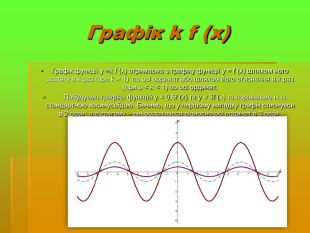
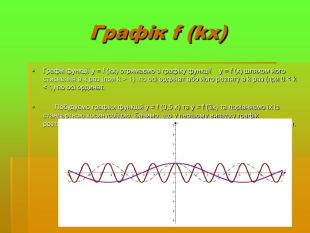
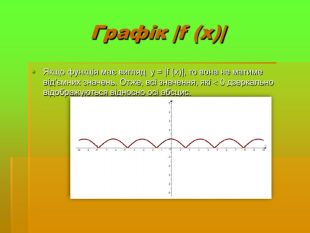
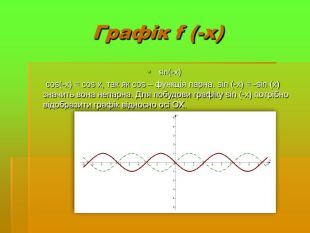
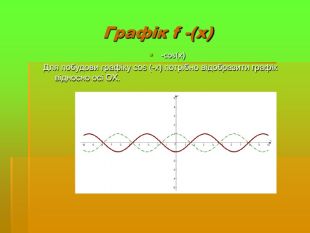
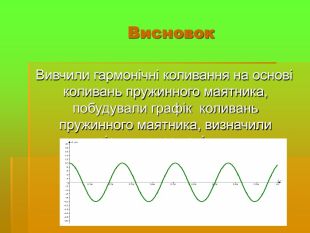
М е т а : Ознайомитися з історією виникнення тригонометричних функцій; Розглянути графік тригонометричних функцій та їх властивості; Дослідити трансформацію графіків тригонометричних функцій; Визначити, де в повсякденному житті, ми можемо зустріти тригонометричні функції та їх графіки.

З м і с т: Історична довідка Тригонометричні функції Трансформація графіків функції Застосування тригонометричних графіків та функцій в фізиці Роль тригонометрії в нашому житті Додатки Використана література та інші джерела

Історична довідка Тригонометрія виникла і розвивалась в давні часи, як один із розділів астрономії. Саме астрономія визначила той факт, що сферична тригонометрія виникла раніше, ніж плоска. Грецький астроном Гіппарх в ІІ ст. до н.е. склав таблицю числових значень хорд в залежності від величин стягуваних ними дуг. Більш повні дані з тригонометрії містяться у відомому «Альмагесті» Птолемея. Птолемей ділив круг на 360 частин, а діаметр на 120 частин. Він вважав, що радіус складається з 60 частин (60ч). Кожну з частин він ділив на 60’, а кожну мінуту на 60”, секунду – на 60 терцій (60”’ ). Отже, він користувався шестидесятиричною системою числення.

Тригонометричні функції Функція y = sin x, її графік та властивості. Графіком функції y = sin x є синусоїда

Властивості синусоїди: Область визначення R. Область значень Період функції = Функція непарна, отже f (x) = 0, при Проміжки знакосталості: sinx 0 на кожному з проміжків виду sinx 0 на кожному з проміжків виду Найбільшого значення, яке дорівнює 1, набуває в точках виду: Найменшого значення, яке дорівнює -1,набуває в точках виду : . Функція зростає на кожному з проміжків Функція спадає на кожному з проміжків

Тригонометричні функції Функція y = cosx, її графік та властивості. Графіком функції y = cosx є косинусоїда.

Властивості косинусоїди: Область визначення R. Область значень Період функції = Функція парна, отже – cos (-x) = cosx. f (x) = 0, при Проміжкизнакосталості: cosx 0 на кожному з проміжків виду cosx 0 на кожному з проміжків виду Найбільшого значення, яке дорівнює 1, набуває в точках виду Найменшого значення, яке дорівнює -1,набуває в точках виду Функція зростає на кожному з проміжків Функція спадає на кожному з проміжків .

Тригонометричні функції Функція y = tg x, її графік та властивості. Графіком функції y = tg x є тангенсоїда.

Властивості тангенсоїди: Область визначення  R крім чисел виду Область значень R. Період функції = . Функція непарна, отже – tg (-x) = - tgx. f (x) = 0, при Проміжки знакосталості: tgx 0 на кожному з проміжків виду tgx 0 на кожному з проміжків виду Найбільшого значенняі найменшого значення не набуває. Функція зростає на кожному з проміжків .

Тригонометричні функції Функція y = ctg x, їїграфік та властивості. Графіком функції y = ctgx є котангенсоїда.

Властивості котангенсоїди: Область визначення  R крім чисел виду Область значень R. Період функції = Функція непарна, отже – ctg (-x) = - ctgx. f (x) = 0, при Проміжки знакосталості: ctgx 0 на кожному з проміжків виду ctgx 0 на кожному з проміжків виду Найбільшого значенняінайменшого значення не набуває Функція спадає на кожному з проміжків

Трансформація графіків функцій Трансформація графіків тригонометричних відбувається шляхом їх розтягнення та стиснення, переміщення графіка відносно осей абсцис та ординат та дзеркального відображення відносно осі абсцис. Наглядно приводити приклад трансформації цих графіків будемо на зразку косинусоїди.

Графік f (x) ± b Графік функції у = f (x)±b отримаємо з графіку функції у = f(x) паралельним переносом на (b) одиниць по осі ординат. Побудуємо графік у = cos(x) + 2. Бачимо, що графік перемістився на 2 одиниці вгору.

Графік f (x ± b) Графік функції у = f (x+b) отримаємо з графіку функції у = f(x) паралельним переносом на (-b) одиниць по осі абсцис. Побудуємо графік функції у = cos(x + 2). Бачимо, що графік перемістився на 2 одиниці вліво.

Графік k f (x) Графік функції у =k f (x) отримаємо з графіку функції у = f (x) шляхом його розтягу в k раз (при k > 1) по осі ординат або шляхом його стиснення в k раз (при 0 < k < 1) по осі ординат. Побудуємо графіки функцій у = 0,5f (x) та у = 3f (x) та порівняємо їх із стандартною косинусоїдою. Бачимо, що у першому випадку графік стиснувся в 2 рази, а в другому – він розтягнувся відносно осі ординат в 3 рази.

Графік f (kx) Графік функції у = f (kx) отримаємо з графіку функції у = f (x) шляхом його стиснення в k раз (при k > 1) по осі ординат або його розтягу в k раз (при 0 < k < 1) по осі ординат. Побудуємо графіки функцій у = f (0,5 x) та у = f (3x) та порівняємо їх із стандартною косинусоїдою. Бачимо, що у першому випадку графік розтягнувся в 2 рази, а в другому – він стиснувся відносно осі абсцис в 3 рази.

Графік |f (x)| Якщо функція має вигляд у = |f (x)|, то вона не матиме від’ємних значень. Отже, всі значення, які  0 дзеркально відображуються відносно осі абсцис.

6 Графік f (|x|) Так, як cos (x) – парна функція, то її графік залишається без змін, а sin (x) змінюється таким чином:

Графік f (-x) sin(-x) cos(-x) = cos x, так як cos – функція парна. sin (-x) = -sin (x) значить вона непарна. Для побудови графіку sin (-x) потрібно відобразити графік відносно осі ОХ.

Графік f -(x) -cos(x) Для побудови графіку cos (-x) потрібно відобразити графік відносно осі ОХ.

Застосування тригонометричних графіків та функцій в фізиці Ми вивчили застосування тригонометричних графіків в фізиці, на прикладі гармонічних коливань. Експериментально довели на прикладі лабораторної роботи.

Лабораторна робота Хід роботи: Закріпили пружину в лапці штатива і підвісили до неї вантаж масою 5 кг. Поряд з вантажем закріпили вертикально вимірювальну лінійку і відмітили початкове положення вантажу. Відхилили пружину від положення рівноваги на 10 см і відпустили. Зафіксували час 10, 15, 20 повних коливань тягарця. За формулами (2) і (3) обчислили період і частоту коливань. За формулою (4) обчислили циклічну частоту коливань. Дослід повторили тричі.

Результати вимірювань та обчислень записали до таблиці Номер досліду N t, c T, c ν, Гц ω, с-1 1 10 8.41 0.841 1.18 7.46 2 15 12.37 0.824 1.21 7.62 3 20 16.38 0.819 1.22 7.66 За результатами вимірювань та обчислень побудували графік залежності А(t) і визначили рівняння гармонічних коливань:

Висновок   Вивчили гармонічні коливання на основі коливань пружинного маятника, побудували графік коливань пружинного маятника, визначили рівняння гармонічних

Застосування тригонометрії в повсякденному житті Тригонометрія допомагає нашому мозку визначати відстані до об'єктів.   Американські вчені стверджують, що мозок оцінює відстань до об'єктів, вимірюючи кут між площиною землі і площиною зору. Такий висновок був зроблений після серії експериментів, учасникам яких пропонувалося поглянути на навколишній світ через призми, що збільшують цей кут.