Індивідуальні завдання з алгебри для учнів з низьким рівнем знань
Індивідуальні завдання для учнів 7 класу
Многочлени
Многочленом називається сума кількох одночленів.
Записувати члени многочленів можна в різній послідовності.
Многочлен , кожний член якого записаний у стандартному вигляді та не має собі подібних, називають стандартним.
Записати суму одночленів 1) 4а і 0,9b; 4а + 0,9b,
- -4а2 і 2m; -4а2 + 2m,
- -3,5m2 і 5,4а;
-
7,5а і -
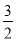 n;
n;
- 5,4а і 0,9b.
Підкресли подібні члени многочлена
11а2 +4ав - 9а2-2ав;
3ав + 8ав +3а2 – 2в2,
0,8х3 -5х2 +6х2 -0,3х3,
3ху – 2а2в + 5ху – 5а2в.
Звести подібні члени многочлена
1)18а – 15а = 3а; 4) 17m -14m =
2) -12b + 5b = -7b; 5) -24а + 20а =
3) 14а2 - 29а2 = -15а2; 6) 12n2 -25n2 =
Додавання і віднімання многочленів
Щоб додати многочлени, достатньо записати їх суму, розкрити дужки і звести подібні доданки
Зразок:
Додати многочлени: 4х2 + 9х – 2 і -7х2 -12х +8,
(4х2 + 9х – 2) + (-7х2 -12х +8) = 4х2 + 9х – 2 - 7х2 -12х +8 =
-3х2-3х-4.
Виконай додавання многочленів
- 2а +3в і 4а – 5в;
- 4х + 4х2 -13 і 2х +13;
- 7х + 2у -5 і 5х – 4у ;
- 7а – 8в + 6с і 8а - 5в + 4с;
Щоб відняти многочлени, достатньо записати їх різницю, розкрити дужки і звести подібні доданки
Зразок:
Від многочлена 2х3 + 9х2 - 3х +12 відніми многочлен
х3 - 3х2 + 7х – 9.
(2х3 + 9х2 - 3х +12) – ( х3 - 3х2 + 7х – 9) = 2х3 + 9х2 - 3х +12 – х3 + 3х2 - 7х + 9 = х3 + 12х2 - 10х + 21
Виконай віднімання многочленів
- 2а +3в і 4а – 5в;
- 4х + 4х2 -13 і 2х +13;
- 7х + 2у -5 і 5х – 4у ;
- 7а – 8в + 6с і 8а - 5в + 4с;
Множення одночлена на многочлен
Щоб помножити одночлен на многочлен, потрібно одночлен помножити на кожен член многочлена й одержані добутки додати .
Помножимо одночлен 2в2 на многочлен 3в3 - 2в + 1
Зразок
2в2 ∙ (3в3 - 2в + 1) = 2в2 ∙ 3в3 + 2в2 ∙ ( - 2в)+ 2в2 ∙1 = 6в5 – 4в3 + 2в2 ;
-3а ( а3 + а – 5) =(-3а) ∙ а3 +(-3а)∙а + (-3а)∙(-5) = -3а4 -3а2 +15а.
Виконай множення:
- х(а +в);
- –у (m– n);
- -3b3(b– 4b2);
- (8а2 – 4а +16)∙ 0,25;
- -4х( х4 –х2 – 8).
Множення многочлена на многочлен
Щоб помножити многочлен на многочлен , досить кожний член одного многочлена помножити на кожний член іншого многочлена і знайдені добутки додати.
Зразок
а) (т + п) (а - 2) = ma -2m + na -2n;
б) (3 - а) (Ь + с - 5) = 3b +3c -15 –ab –ac + 5a;
в) (4m -n + 1) (х - 2у) = 4mx -8my –nx +2ny +x -2y;
г) (7а – 3b) (2а - 5с) = 14a2 -35ac -6ab +15bc.
Виконай за зразком множення многочленів
а) (х - 2) (2х + 1);
б) (За - 1) (а2 + а - 2);
в) (5 - Зу) (у2 + Зу - 4);
г) (b2 + 4b) (7b - 1). '
Формули скороченого множення
Різниця квадратів двох виразів
(а – b) ( а + b) = а2 - b2
Добуток різниці двох виразів і їх суми дорівнює різниці квадратів цих виразів
Зразок
а) (а + 4) (а - 4) = а2 - 16; б) (3 - b) (b + 3) = 9 – b2
в) (5т - 2n) (5т + 2n) = 25m2 - 2n2 г) (7а + b)(b - 7а) = b2- 49а2;
д)(- 9х - у)(- у + 9х) =(81х 2- у2); е)(х5у2 - а3)(а3+х5у2) =х10у4 – а6.
Виконай множення використовуючи формулу різниці квадратів:
- (3 –х)(3 +х);
- (7а +b)(b- 7а);
- (2х – у) (2х +у);
- (0,5m -10n) (0,5m + 10n);
- (-7х - у )(7х – у);
- (5а -3b)(5а +3b).
Квадрат суми двох виразів
Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів і плюс квадрат другого виразу
( а + b)2 = а2 +2аb +b2
Зразок
( 4 + х)2 = 42 + 2∙4∙х + х2 = 16 +8х +х2;
(у + 6)2 = у2 + 2∙у∙ 6 + 62 = у2 +12у +36;
(3а +5)2 = (3а)2 +2∙ 3а∙5 +52 = 9а2 +30а +25;
(0,2а + 0,3b)2 = (0,2а)2 +2∙0,2а∙0,3b + (0,3в)2 =0,04а2 +0,12аb +0,09b2.
Піднеси до квадрата за зразком
- (у + 5)2;
- ( 2m +4)2;
- ( х + 6) 2;
- ( 0,5а + 2b) 2
Квадрат різниці двох виразів
Квадрат різниці двох виразів дорівнює квадрату першого виразу
мінус подвоєний добуток цих виразів і плюс квадрат другого виразу
( а - b)2 = а2 - 2аb +b2
Зразок
( х – 5)2 = х2 -2∙ х∙5 +52 ==х2 -10х +25;
( 8 – n)2 = 82 – 2∙8∙n +n2 =64 -16n +n2;
(2х – 3у)2 =( 2х)2 -2∙2х∙3у +(3у)2 =4х2 -12ху + 9у2.
Піднеси до квадрата за зразком
- (7 – а)2 ;
- ( 5а – 2х)2;
- (х - 2у)2;
- (0,3а - 0,4b)2.
Лінійне рівняння з однією змінною
Рівняння виду ах = b, де а і b – довільні дійсні числа, називаємо лінійним рівнянням з однією змінною.
Основні властивості рівнянь:
а) Будь - який член рівняння можна перенести з однієї частини рівняння в іншу, змінивши його знак на протилежний.
б) Обидві частини рівняння можна помножити або поділити на одне й те ж саме число, відмінне від нуля.
в) Рівняння називаються рівносильними, якщо вони мають однакові корені.
Алгоритм розв’язування рівняння
- Перенеси доданки , які містять невідоме, у ліву частину рівняння, а відомі у праву частину змінивши їхні знаки на протилежні.
- Виконай додавання подібних доданків.
- Поділи ліву і праву частини рівняння на коефіцієнт при невідомому, якщо він не дорівнює нулю.
Зразок : 1) 8х -3= 5х +6; 2) х – 7 + 8х = 9х - 3 - 4х;
8х - 5х = 6 + 3; х + 8х - 9х + 4х =-3 +7;
3х = 9; 4х = 4;
х= 9 : 3; х = 4: 4;
х = 3. х = 1.
За даними зразками розв’яжи рівняння:
а) 2х – 19 = 7х + 31 ;
б) 11х + 42 – 2х = 100 - 9х - 22;
в) -7,1х + 2,4 = 2,8 - 4,2 -9х;
г) 3х - 20 + 6х – 2 = 8х – 10 +2х.
Розв'язування рівнянь, які зводяться до лінійних
При розв’язуванні рівнянь , які зводяться до лінійних використовуватимемо такий алгоритм:
- Розкрити дужки.
- Перенести невідомі доданки в ліву частину частину рівняння, відомі - у праву, змінивши їх знаки на протилежні.
- Виконай зведення подібних доданків.
- Поділи ліву і праву частини рівняння на коефіцієнт при невідомому, якщо він не дорівнює нулю.
Зразок розв’язування рівняння:
1)15(х+2) = 6(2х + 7); 3) (16 – 3х) – (5х +3) = 12 – (7 + 4х);
15х + 30 = 12х + 42; 16 – 3х - 5х -3 = 12 – 7 - 4х;
15х – 12х = 42 -30; -3х – 5х + 4х = 12 – 7 -16 +3;
3х = 12; - 4х = - 8;
х = 12 : 3; х = (-8) : (-4);
х = 4. х = 2.
2) 10у – 2(7у – 2) = 5(4у + 3) +3у;
10у – 14у + 4 = 20у + 15 +3у;
10у - 14у – 3у = 15 – 4;
-7у = 11;
у = ![]() .
.
За зразком розв’яжи рівняння:
а) 5(х + 3) = 8( 10 – х);
б) 2(5у – 2) = 3(2у – 1) – 9;
в) 4у – 3(20 – у) = 6у- 7( 11 – у);
г) (6х -2) – (5 -2х) = - (4х + 19).
Степінь з натуральним показником
Степенем числа а з показником n називається добуток n рівних множників, кожний з яких дорівнює а.
Записуємо аn - число а називають основою степеня, число n – показником степеня. Наприклад 62 = 66 =36, 82 = 88 =64, 122 =12 12 = 144,
43=444=64,25=22222=32,33= 333=27.
Основою степеня а може бути довільне число
32 =3∙3= 9 (-3)2 = (-3) (-3) = 9
53 = 5∙5∙5= 125 (-5)3= (-5) (-5) (-5) = -125
34 = 3∙3∙3∙3 =81 (-3)4 =(-3) (-3) (-3) (-3) =81
0,32 = 0,3∙ 0,3 = 0,09 (- 0,3)2 = (-0,3) (-0,3) = 0,09
Згадаємо: парний степінь від’ємного числа – число додатне, непарний степінь від’ємного числа – число від’ємне.
Запиши добутки у вигляді степеня
а∙а∙а∙а∙а∙а∙а∙а; 5∙5∙5∙5∙5∙5∙5; 3∙3∙3∙3∙3∙3; у∙у∙у∙у∙у; 0,2∙0,2∙0,2∙0,2∙0,2
Обчисли : 24; (0,6)2 ;( -5)2 ; 32 ;43 ; 0,13 ;
(- 2)4; (-0,6)2 ; 52 ; (-3)2 ; (-4)3 ; (- 0,1)3 .
Властивості степеня з натуральним показником
Примноженні степенів з однаковою основою показники додаємо,а основу залишаємо ту саму.
аm∙аn = аm+n
Зразок 1) 32∙33 = 3 2+3= 35 ; 2) 59 ∙ 58 ∙52=5 9+8+2=519 ; 3) с7 с4 с = с 7+4+1
4)х4 ∙х2 = х 4+2=х6; 5) 0,2 4 ∙ 0,23 = 0,2 4+3 = 0,2 7
Виконай множення степенів за зразком 1) 23 ∙24; 2) 57∙54∙52; 3) 82∙84∙8; 4)х2 ∙х3; 5)а6∙ а4∙а2 ; 6) 0,32∙0,34.
При діленні степенів з однаковою основою показники віднімаємо, а основу залишаємо ту ж саму
аm:аn = аm - n
Зразок 1) 35:33 = 3 5-3= 32 ; 2) 59 : 55 : 52= 5 9-5-2 = 52 ; 3) с8 :с3: с = с 8-3-1
4)х4 ∙:х2 = х 4-2=х2; 5) 0,2 5 : 0,23 = 0,2 5-3 = 0,22
Виконай ділення степенів 1)712: 75; 2)316: 38; 3)378:377 ; 4) а9: а5; 5) х14: х6: х; 6) 1,29:1,25
При піднесенні степеня до іншого степеня показники степенів перемножуємо, а основу залишаємо ту ж саму.
(аm)n =аm∙n
Зразок 1) (а5)3 = а5∙3 = а15; 2) ( -х3)4 = - х 3∙4 = -х12 = х12;
3) ( 92)5 = 9 2∙5 =910; 4) (0,24)6 = 0,24∙6 =0,224.
Виконай піднесення до степеня за зразком
- (78)2 ; 2) ( а5)3; 3) (у4)5; 4) (0,57) 4; 5) (-а5)4; 6) (а10)3.
При піднесенні добутку до степеня підносимо до цього степеня кожний співмножник.
(аb)m = аm ∙ bm
Зразок (ав)8 =а8в8; (2х)5 =25х5 ; (аху)10 = а10х10у10;
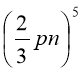 =
= 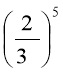 p5n5
p5n5
Виконай піднесення добутку до степеня за зразком
(ау)6 ; (5х)2 ; (авс)12; ( 0,4ха )7
При піднесенні дробу до степеня чисельник і знаменник підносимо до того самого степеня.
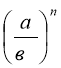 =
= ![]()
Зразок ![]() =
= ![]() ;
; ![]() =
= ![]() ;
;
Виконай піднесення дробу до степеня за зразком
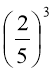 ,
, 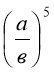 ,
,![]()
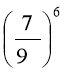 ,
, 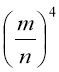 .
.


про публікацію авторської розробки
Додати розробку
