Інформаційні картки до теми "Многогранники"
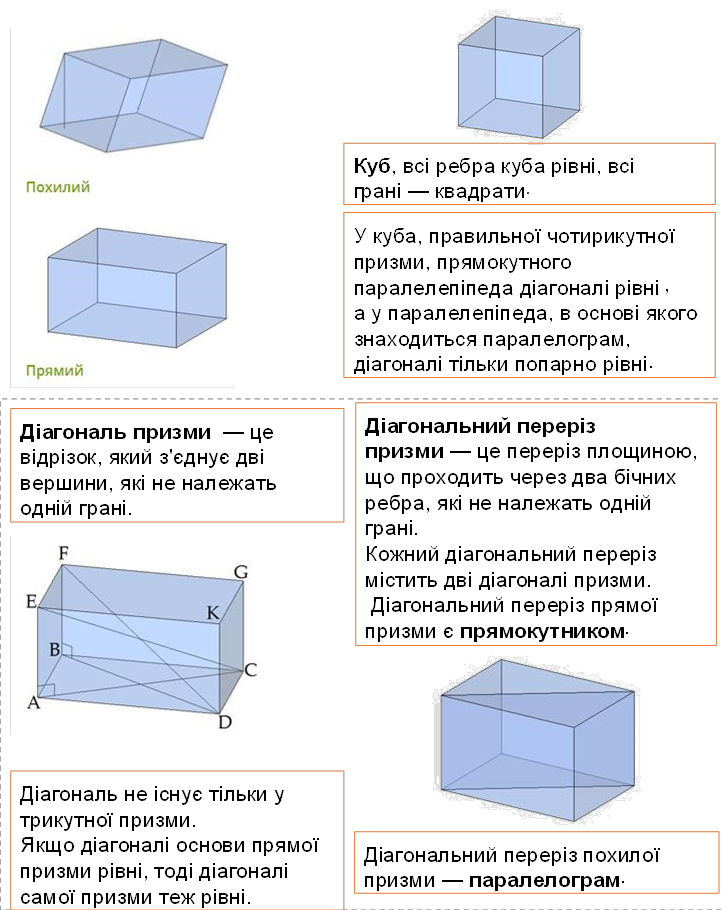
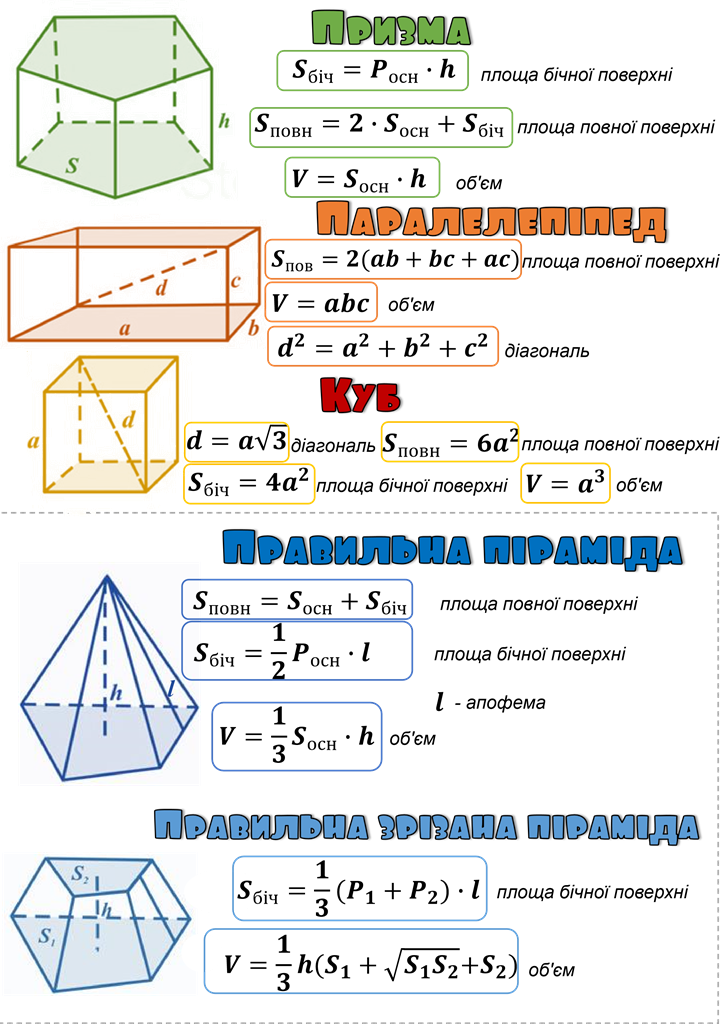
це многогранник, дві грані якого є рівними многокутниками, що знаходяться в паралельних площинах, а інші грані — паралелограми.
Грані, які знаходяться в паралельних площинах, називаються основами призми, а інші грані — бічними гранями призми.
Залежно від основи призми бувають: трикутні чотирикутні шестикутні та ін.
 |
Призма з бічними ребрами, перпендикулярними її основам, називається прямою призмою. Пряма призма називається правильною, якщо її основи — правильні многокутники.
Висота прямої призми збігається з боковим ребром.
Призма, бічні ребра якої не перпендикулярні основам, називається похилою призмою.
Висота похилої призми — це перпендикуляр, проведений між основами призми. Часто перпендикуляр проводять з однієї з вершин верхньої основи.
|
це чотирикутна призма, всі грані якої є паралелограмами. |
|
Пряма призма, основою якої є прямокутник, називається прямокутним паралелепіпедом. |
 |
Види паралелепіпедів
|
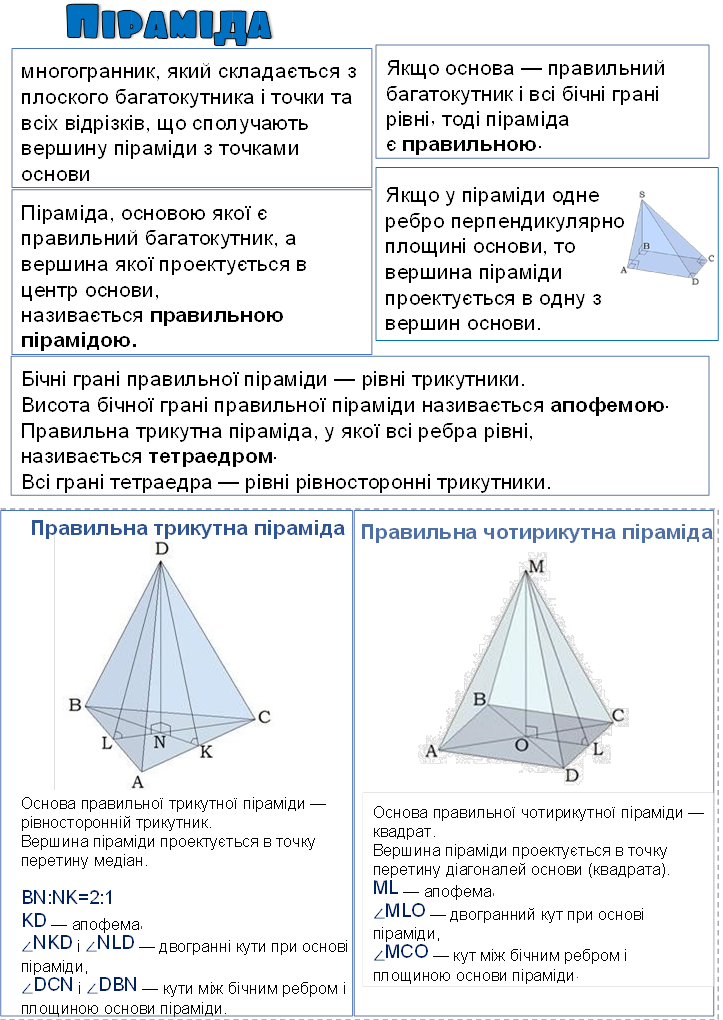
Якщо бічні грані піраміди з її основою утворюють рівні двогранні кути, тоді всі висоти бічних граней піраміди рівні (у правильної піраміди це апофеми), вершина піраміди проектується в центр кола, вписаного в багатокутник основи |
|
Якщо бічні ребра піраміди з площиною основи утворюють рівні кути, тоді ребра піраміди рівні, вершина піраміди проектується в центр кола, описаного навколо багатокутника основи. |
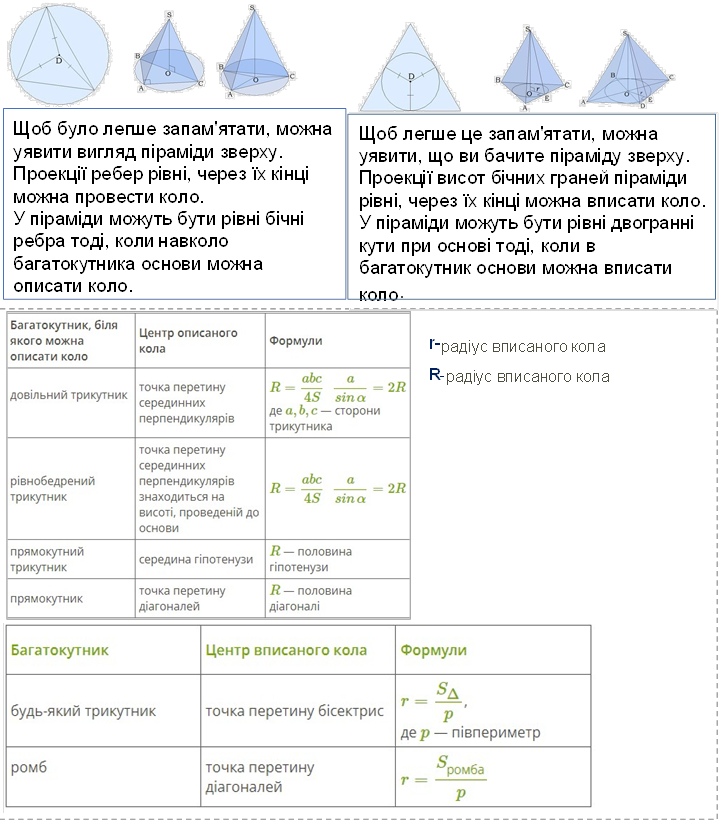
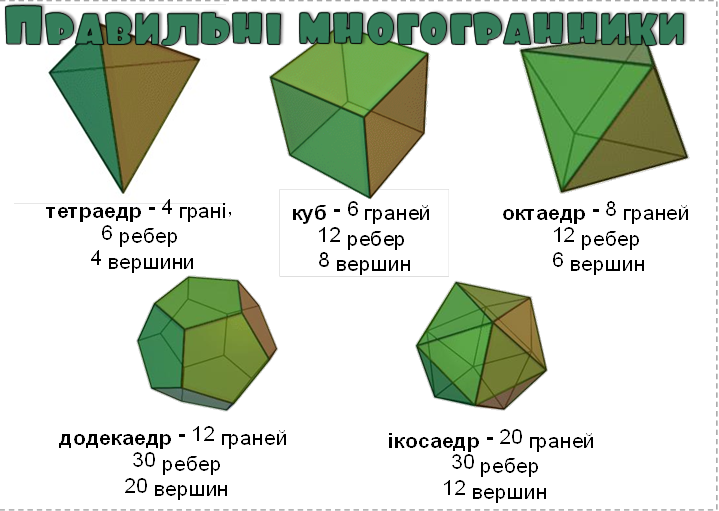
Опуклий многогранник називається правильним, якщо:
1. усі його грані - рівні правильні многокутники;
2. у кожній його вершині сходиться одне і те ж число ребер.
Всі ребра правильного многогранника рівні, а також рівні всі двогранні кути, що містять дві грані зі спільним ребром.
1. У правильного n-кутника, якщо n≥6, кути не менш 120°.
2. У кожній вершині многогранника повинно бути не менше трьох кутів.
3. Навіть при трьох кутах сума всіх кутів вже досягає 360°.
4. 
Сума всіх плоских кутів при кожній вершині опуклого многогранника менше 360°.
Отже, не існує правильного многогранника, гранями якого були б правильні nкутники, якщо n≥6.
Тільки правильні трикутники, чотирикутники (квадрати) і п'ятикутники можуть бути гранями правильного многогранника.
Теорема Ейлера.
У будь-якому опуклому многограннику сума числа граней і числа вершин на 2 більше числа ребер.
-
Перейменуйте з "многогранники" на "багатогранники"
про публікацію авторської розробки
Додати розробку