ІНТЕГРОВАНЕ НАВЧАННЯ ТА МІЖПРЕДМЕТНІ ЗВ’ЯЗКИ НА УРОКАХ ФІЗИКИ

 

Вступ

 

Реформування системи освіти в Україні нині набуло глобального характеру. Ми є свідками процесів, які безпосередньо пов’язані з реформуванням змісту освіти. Формування компетентностей учнів зумовлене не тільки реалізацією відповідного оновленого змісту освіти, але й впровадженням інноваційних методів та технологій навчання. Якісне навчання забезпечує засвоєння знань та формування умінь, що для випускника школи стануть підґрунтям у його подальшому житті. Продуктом школи є людина, особистість. Тож навчати її треба так, щоб учень відчув, що знання та вміння є для нього життєвою необхідністю. Навчальна діяльність у кінцевому підсумку повинна не просто дати людині суму знань, умінь і навичок, а сформувати її компетенції, визначити шлях до самовдосконалення. У світлі сучасних завдань всебічно, гармонійно розвиненої особистості школяра проблема міжпредметних зв’язків набуває важливого значення. Актуальність даної проблеми зумовлена розвитком науки, техніки, суспільства.Вивчення фізики, як і будь-чого іншого, потребує мотивації. Тобто учень (та й учитель) мають розуміти, відчувати, навіщо вони вивчають і викладають фізику. Тому навчання фізики в основній школі має бути максимально наближеним до вікових пізнавальних можливостей учнів, постійно стимулювати їхній інтерес до навчання і самоосвіти. Використання математичного апарату та знань з інших предметів має сприяти міцному й більш сприятливому вивченню питань фізики, а не обтяжувати й ускладнювати їх. Я.А.Коменський зазначав, що необхідно «завжди і всюди брати разом те, що пов’язано одне з одним». Необхідність такого підходу до організації навчально-виховного процесу він пояснював тим, що «всі знання виростають з одного коріння – навколишньої дійсності, мають між собою зв’язки, а тому повинні вивчатися у зв’язках». Великий педагог Ушинський К.Д. вважав, що одним з шляхів досягнення високої якості знань є злиття дисциплін, що вивчаються. Це злиття передбачає порядок і єдність, координацію між елементами знань. Доки різні предмети навчального курсу будуть викладатися, ніби зовсім не знаючи про існування один одного, учіння не буде суттєво впливати на розвиток дітей; доти учіння буде не захоплюючим органічним процесом психічного розвитку, а нестерпно нудною працею для учня. Відомий китайський філософ Конфуцій сказав: «Три шляхи ведуть до знань: шлях роздумів – це шлях найблагородніший, шлях наслідування – найлегший, і шлях дослідження - найскладніший».

У своїй роботі вчитель повинен керуватися двома шляхами: роздумів і дослідження, бо, ідучи сліпо шляхом наслідування, він утратить себе як творець і мислитель.

Міжпредметна інтеграція – перспективний напрямок реалізації новітніх технологій, де визначальною умовою є сукупність таких методичних підходів, які програмують позицію учня як активного співтворця уроку.

Беручи в основу своєї педагогічної роботи принцип інтеграції, переконаний, що цей метод створює сприятливі умови для формування в учнів цілісної картини світу, вироблення здатності сприймати предмети і явища всебічно, системно, емоційно.

 

 

 

 

 

 

 

 

 

 

 

Розділ І. Інтегроване навчання та міжпредметні зв’язки на уроках: спільне, відмінне, особливості реалізації

 

1.            Сутність поняття «міжпредметні зв’язки» та інтегроване навчання

 

Ідея об’єднання в рамках одного уроку (одного предмету) декількох різних підходів та поглядів на одну й ту саму тему, поняття, процес, явище не є принципово новою. Ще в працях Я. А. Коменського акцентується увага на необхідності «завжди і всюди брати разом те, що пов’язано одне з одним»  Необхідність інтегрованого підходу до організації навчально-виховного процесу великий дидакт пояснював таким чином: «Всі знання виростають з одного коріння – навколишньої дійсності, мають між собою зв’язки, а тому повинні вивчатися у зв’язках».

Довгий час терміни «міжпредметні зв’язки» та «інтеграція навчального матеріалу» вживалися як синоніми. Проте згодом намітилася їх диференціація: «у тих випадках, коли один предмет є основним, а відомості з іншого викладаються лише в допоміжній ролі з метою повторення, прискорення процесу навчання чи закріплення знань, умінь і навичок є підстава говорити про міжпредметні зв’язки. Інтеграція – це створення нового цілого на основі виявлення однотипних елементів і частин у кількох раніше різних одиницях, пристосування їх у раніше неіснуючий моноліт особливої якості».

У Великому тлумачному словнику сучасної української мови зазначається, що «інтеграція це – доцільне об’єднання та координація дій різних частин цілісної систем». Словосполучення «інтеграція навчання» у Педагогічному словнику тлумачиться як «відбір та об’єднання навчального матеріалу з різних предметів з метою цілісного, системного й різнобічного вивчення важливих наскрізних тем (тематична інтеграція); це створення інтегрованого змісту навчання – предметів, які об’єднували б в єдине ціле знання з різних галузей.Характеризуючи міжпредметні зв’язки, слід зазначити, що у Педагогічному словнику вони тлумачаться як «дидактичний засіб, який передбачає комплексний підхід до формування й засвоєння змісту освіти, що дає можливість здійснювати зв’язки між предметами для поглибленого, всебічного розгляду найважливіших понять, явищ». В Українському педагогічному словнику міжпредметні зв’язки тлумачаться як «взаємне узгодження навчальних програм, зумовлене системою наук і дидактичною метою» . На думку авторів словника, міжпредметні зв’язки відображають комплексний підхід до виховання й навчання, який дає можливість виділити як головні елементи змісту освіти, так і взаємозв’язки між навчальними предметами.

Питанням інтегрованого навчання та організації міжпредметних зв’язків на уроках присвячено багато праць українських вчених. Так, наприклад, уроки інтегрованого змісту та уроки з використанням міжпредметних зв’язків, О. Я. Савченко також розглядає як різні дидактичні поняття, оскільки міжпредметні зв’язки передбачають включення в урок запитань і завдань з матеріалу інших предметів, що мають допоміжне значення для вивчення певної теми. Це, на думку науковця, окремі короткочасні моменти уроків, які сприяють глибшому сприйманню та осмисленню якогось конкретного поняття. Натомість під час інтегрованого уроку «учні ознайомлюються зі змістом різних предметів, включаються у несхожі між собою види діяльності, що підпорядковані одній темі».

Враховуючи все вищесказане можна схематично зобразити порівняльну характеристику інтегрованого навчання та навчання з міжпредметними зв’язками.

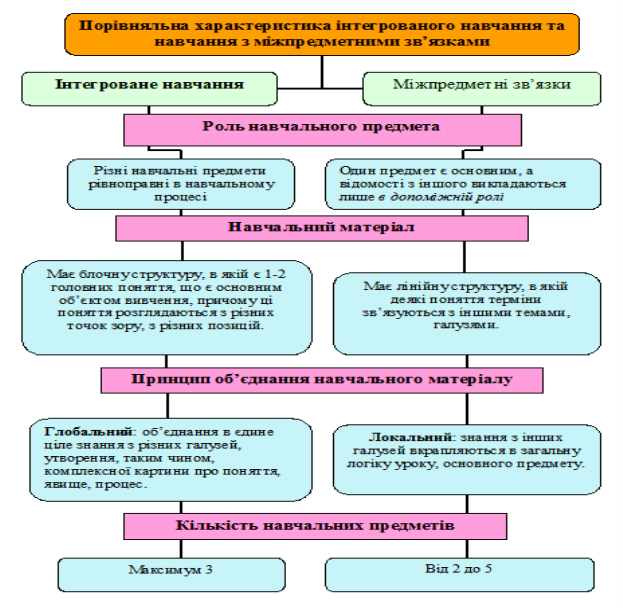
Ідея реалізації інтегративного підходу до навчання та міжпредметних зв’язків на уроках – важливий фактор, що сприяє підвищенню якості навчально-виховного процесу в школі. Реалізація міжпредметних зв’язків та проведення інтегрованих уроків сприяє розкриттю творчих здібностей кожного вчителя, урізноманітненню методів та організаційних форм навчання для посилення інтересу учнів до знань, активізації мислення, оволодіння системою наукових знань і, зрештою, підвищення результативності всієї навчально-виховної роботи.

 

 

 

 

1.2. Роль та функції міжпредметних зв’язків,  інтегрованого навчання у навчальному процесі

 

В наш час актуальною стала проблема підвищення зацікавленості учнів навчальними предметами. Крім цього – назріла необхідність застосування отриманих знань на практиці. Потрібно, щоб учні отримували певні знання та навички не для накопичення знань, а щоб вони могли їх застосувати в подальшому житті. Цей далеко неповний перелік проблем змушує педагогів, шукати різні напрямки роботи з дітьми. Один з дієвих засобів – це застосування на уроках між предметних зв’язків та проведення інтегрованих уроків.

Сьогодні у зв’язку із збільшенням об’єму інформації, яка підлягає засвоєнню в період навчання у школі, а також з необхідністю ознайомлення учнів з основами самоосвіти, важливого значення набуває вивчення ролі міжпредметних зв’язків. У сучасній системі наук чітко намітився процес взаємного проникнення та зв’язку між науками. Це цілком об’єктивний процес, який обумовлений єдністю навколишнього світу. Розвиваючись, кожна наука не лише поглиблює свої знання про суть предмета, що вивчається, але і розширює межі своїх досліджень.

Міжпредметні зв’язки в навчанні відображають комплексний підхід до виховання і навчання, дозволяють вичленувати головні елементи змісту освіти. Вони формують як конкретні знання учнів, так і розкривають гносеологічні проблеми, без яких неможливе системне засвоєння основ наук.

Проблему міжпредметної інтеграції можна віднести до числа традиційних, що стали вже класичними проблемами педагогіки.

У зв'язку з модернізацією змісту освіти особливого значення набуває професійна компетентність сучасного педагога, переорієнтація його мислення на усвідомлення принципово нових вимог до педагогічної діяльності.

У навчальному процесі під час реалізації міжпредметних необхідно дотримуватися таких вимог:

•            взаємозв'язки дисциплін повинні здійснюватися і використовуватися на всіх етапах навчального процесу систематично (під час вивчення нової навчальної інформації, завдань самостійної роботи, контролю знань, умінь і навичок тощо);
•            під час реалізації міжпредметних зв'язків дисципліни мають зберігати свою відносну самостійність, відповідний науковий рівень, логічну структуру предмета, послідовність вивчення навчального матеріалу;
•            зв'язки різних предметів повинні забезпечувати всебічне вивчення й інтенсивний обмін навчальною інформацією, формування на основі вищого рівня узагальненості єдиної  картини світу та компетентностей учнів;
•            навчальна інформація, засвоєна під час вивчення інших дисциплін, не повинна дублюватися, а має використовуватися з метою мотивації навчальної діяльності учнів, актуалізації опорних знань, умінь і навичок, обґрунтування, з'ясування сутності явищ, моделювання процесів тощо.Міжпредметні зв’язки спонукають учнів до активної пізнавальної діяльності. Сучасний урок вимагає від учителя постановки проблемних ситуацій (задач), а від учня – самостійної роботи щодо їх вирішення (пізнання нового).Встановлюючи зв’язки між предметами, учні узагальнюють, синтезують здобуті знання. Якщо ж ці знання будуть підґрунтям для вирішення комплексних пізнавальних проблем, це активізує мисленнєву діяльність учнів, сприятиме подальшому засвоєнню навчального матеріалу, розвиватиме мотиваційну та когнітивну сфери особистості учня.

Теоретичні основи проблемного навчання обґрунтовані А. П. Корнієвим, В. Т. Кудрявцевим, О. М. Топузовим, А. В. Фурманом. Міжпредметні зв’язки досліджують Н. М. Захарова, Н. В. Лесняк, О. В. Тесленко та ін. Проблема поєднання міжпредметних зв’язків і проблемного навчання у навчально-виховному процесі була започаткована В.М.Максимовою.

Встановлюючи міжпредметні зв’язки, учні краще розуміють і засвоюють навчальний матеріал. Міжпредметні зв’язки вимагають від школярів розуміння понять та термінів, ґрунтовних знань, умінь робити висновки та узагальнення, встановлювати причинно-наслідкові зв’язки. Якщо міжпредметні зв’язки є підставою для вирішення будь-яких пізнавальних задач і, як наслідок, комплексних навчальних проблем, то слід говорити про використання у навчанні проблемного підходу.Побудова уроків із використанням міжпредметних зв’язків ведуть до підвищення наукового рівня навчання, сприяють залученню школярів до системного методу мислення, розширюють сферу пізнання, поєднуючи елементи знань з різних навчальних дисциплін, забезпечують систему в організації предметного навчання, спонукають учителя до самоосвіти, творчої взаємодії з іншими вчителями-предметниками.

Причини труднощів практичного здійснення міжпредметних зв’язків носять як об’єктивний так і суб’єктивний характер. Об’єктивна причина – недостатня кількість методичного матеріалу, суб’єктивні – необізнаність із змістом програм суміжних предметів, відсутність досвіду в реалізації зв’язків між предметами, здійснення міжпредметних зв’язків не в повній мірі.

У новому Державному стандарті базової та повної загальної середньої освіти відмічається важливість міжпредметних зв’язків у формуванні системи знань учнів.Формування математичної компетентності у курсі фізики передбачає 

Уміння:

• застосовувати математичні методи для опису, дослідження фізичних явищ і процесів, розв’язування фізичних задач, опрацювання та оцінювання результатів експерименту;
• розуміти й використовувати математичні методи для аналізу та опису фізичних моделей реальних явищ і процесів.

Ставлення:

• усвідомлення важливості математичного апарату для опису та розв’язання фізичних проблем і задач.

Навчальні ресурси:

завдання на виконання розрахунків, алгебраїчних перетворень, побудову графіків, малюнків, аналіз і представлення результатів експериментів та лабораторних робіт, обробка статистичної інформації, інформації наведеної в графічній, табличній й аналітичній формах.

Систематичне здійснення міжпредметних зв’язків математики і фізики  дозволяє підвищити якість математичних та фізичних знань учнів, сприяє формуванню уявлень про методи математичного моделювання, як  методу вивчення реальних явищ, надає можливості для розвитку пізнавальних інтересів учнів.Зв’язки між математикою і фізикою як науками постійні й різноманітні. Об’єктом чистої математики є реальний матеріал: просторові форми і кількісні відношення матеріального світу. Проте, цей матеріал набуває досить абстрактних форм, тобто основним методом математики є метод абстракції. За способом відображення дійсності математика – аспектна наука. Її предметною галуззю є вся дійсність, іншими словами, немає жодної матеріальної області, в якій не проявилися б закономірності, що вивчаються математикою. Таким чином, математика вивчає кількісні співвідношення і просторові форми як існуючих областей об’єктів, так і тих, які можна «сконструювати».

Фізика як наука досліджує фундаментальні властивості матерії в двох її формах –  формі речовини і поля. Вони являють собою комплекс самостійних галузей знання, об’єднаних вихідними принципами, фундаментальними теоріями і методами дослідження.

Спочатку фізика переважно досліджувала властивості оточуючих нас тіл. Проте вже на цьому етапі вивчалися і деякі загальні проблеми – рух , взаємодія тіл, будова речовини, природа і механізм ряду явищ, наприклад теплових, звукових, оптичних. Отже, спочатку фізика була в основному об’єктною наукою. Але, вже у ХХ столітті головним об’єктом фізики стають фундаментальні явища природи і описуючі їх закони. Математика як наука сформувалася першою, але у міру розвитку фізичних знань математичні методи знаходили все більше застосування у фізичних дослідженнях. Тому взаємозв’язок математики і фізики визначаються насамперед наявністю загальної предметної галузі, яка вивчається з різних точок зору.

Взаємозв’язок математики і фізики виражається у взаємодії їхніх ідей і методів. Ці зв’язки можна умовно розділити на три види, а саме:

1. Фізика ставить завдання і створює необхідні для їх вирішення математичні ідеї та методи, які надалі служать базою для розвитку математичної теорії.

2. Розвинена математична теорія з її ідеями і математичним апаратом використовується для аналізу фізичних явищ, що часто стимулює виникнення нової фізичної теорії, яка у свою чергу, призводить до якісного розвитку фізичної картини світу і виникнення нових фізичних проблем.

3. Розвиток фізичної теорії спирається на наявний певний математичний апарат, але останній вдосконалюється і розвивається по мірі його використання у   фізиці. Тісний зв’язок між шкільними курсами математики і фізики є традиційним.  Математика не тільки дає фізиці обчислювальний апарат, але й збагачує її в ідейному плані. На уроках математики учні вчаться працювати з математичними виразами, а завдання викладання фізики полягає в тому, щоб ознайомити їх із переходом від фізичних явищ і зв’язків між ними до їх математичного вираження і навпаки.Реалізація міжпредметних зв’язків фізики й математики сприяє розвитку теоретичного пізнання фізичних об’єктів, оскільки:

1) формується загально-змістовний вигляд досліджуваного об’єкта;

2) виявляються умови походження понять, законів;

3) засвоюються способи отримання нових знань;

4) розкривається сутнісна сторона законів;

5) об’єднуються часткові закони;

6) загальнонаукові методи і прийоми перетворюються в інструмент пізнавальної діяльності;

7) встановлюється зв’язок між предметною реальністю, наочною і абстрактно-математичною формою знань.

Перенесення знань із однієї області науки в різноманітні ситуації інших областей доводить учням те, що сила наукового знання складається в логічній побудові будь-якої його області, в універсальності, загальності фундаментальних положень науки. Засвоєння фундаментальних положень науки, її принципів, уміння отримувати із них частинні випадки і застосовувати їх в споріднених навчальних дисциплінах – є вищим щаблем міцності  знань.

При вивченні фізики значну увагу приділяють розгляду різних величин і законів, завдяки чому створюються сприятливі умови для узагальнення знань у процесі розкриття їх змісту й встановлення зв’язків між ними. Проблему міжпредметних зв’язків слід розглядати насамперед у плані формування світогляду учнів на основі філософського узагальнення знань, що їх здобувають вони при вивченні суміжних дисциплін. Узагальнення знань учнями є важливою умовою глибокого засвоєння навчального матеріалу. Якість засвоєння матеріалу і ефективність формування відповідного типу мислення визначається метою, засобами й способами узагальнення в системі навчальної діяльності.

Міжпредметні зв’язки виконують низку функцій:

•                     методологічна функція полягає в тому, що тільки на її основі можливе формування в учнів сучасних уявлень про історичний розвиток суспільства, цілісність процесів та явищ у світі, багатогранність і різноманітність цивілізацій;
•                     освітня функція міжпредметних зв’язків сприяє формувати системність, усвідомленість знань учнів. Міжпредметні зв’язки виступають як засіб більш глибокому розумінню суспільно-політичних процесів, сприяють засвоєнню історичних понять, формують історичну компетентність підлітків;
•                     розвиваюча функція міжпредметних зв’язків визначається їх роллю у творчому і системному розвитку учнів, у формуванні самостійності, інтересу до історії, минулого;
•                     виховна функція сприяє реалізації комплексного підходу до виховання;
•                     конструктивна функція міжпредметних зв’язків веде до більш активної співпраці вчителів-предметників.

У вітчизняній практиці навчання в загальноосвітніх закладах реалізується на рівні міжпредметних зв’язків. Одним із напрямків міжпредметних зв’язків є інтегровані заняття.

Потреба у виникненні інтегрованих занять пояснюється низкою причин:

• світ, що оточує дітей, пізнається ними через предмети шкільного циклу не як єдність процесів і явищ, знання з окремих предметів не дають уявлення про цілісність світу;
• інтегровані заняття розвивають потенціал учнів, спонукають до пізнання, до осмислення, знаходження причинно-наслідкових зв’язків, розвивають комунікативність, компетентність;
• форма проведення інтегрованих уроків нестандартна, а це активізує підлітків, зацікавлює оригінальністю, залучає до діалогу, дискусії;
• сучасному суспільству потрібні висококваліфіковані спеціалісти, які можуть орієнтуватися в інформаційному просторі і використовувати знання на практиці;
• інтегровані заняття дають можливість учням проявити свою творчість,
• сприяють підвищенню мотивації навчання, формуванню пізнавального інтересу;
• сприяють розвитку мислення, формують вміння аналізувати, узагальнювати;
• інтеграція є джерелом знаходження нових зв’язків між фактами, які поглиблюють знання учнів з предмета.

Форми занять можуть бути різними, щоб діти мали можливість проявити свої "діяльні сили". (І. Г. Песталоцці). Інтеграція в сучасній школі, в навчальних закладах, де надається повна середня освіта, прослідковується на внутрішньо предметному та міжпредметному рівнях, інтегровані заняття вимагають певної підготовки як вчителя так і учнів.

Встановлення зв’язків між предметами веде до формування самостійності мислення, розвиває логічне мислення учнів, яке пов’язане із формуванням інтелектуальних умінь і навичок. Логічне мислення сприяє розвитку мовлення, а увага до мовного оформлення думки робить її точною і логічною.

Нижче подані розробки уроків з різних тем де прослідковуються міжпредметні зв’язки фізики та математики

       Для зручності викладання фізики в різних класах пропоную відібраний матеріал з математики.

 

№	Навчальний матеріал з фізики	Математична база
1.	Властивості тіл. Фізичнівеличини. Вимірювання. Засобивимірювання. Точністьвимірювання. Міжнародна система одиницьфізичних величин.	Метрична система мір.
2.	Вимірювання довжини, площі. Одиниці довжини, площі.	Прямокутник. Квадрат. Площа прямокутника.
3.	Вимірювання об’єму. Одиниці об'єму.	Прямокутний паралелепіпед. Куб. Об’єм прямокутного паралелепіпеда. Одиниці об'єму.
4.	Графіки шляху і швидкості при рівномірному прямолінійному русі.	Графіки прямої і оберненої залежності. Графіки лінійної залежності.
5.	Прості механізми. Важіль. Умова рівноваги важеля. Блоки.	Пропорція.
6.	Простімеханізми. «Золоте правило» механіки. Коефіцієнткорисноїдіїмеханізмів	Знаходження відсоткового відношення двох чисел.
7.	Паралельне з'єднання провідників.	Додавання і віднімання дробів з різними знаменниками.
8.	Шлях, переміщення і координата при прямолінійному  рівноприскореному русі.	Квадратні рівняння. Співвідношення між сторонами і кутами в прямокутному трикутнику.
9.	Додавання і розкладання сил. Рівнодійна. Векторні фізичні величини	Теореми синусів і косинусів Поняття вектора, його модуля. Сума векторів. Поняття про масштаб.
10	Криволінійний рух	Коло, дотична. Центральний кут.
11	Робота сили. Потужність. Енергія	Площа прямокутника,  трикутника. Тригонометричні функції
12	Робота термодинамічного процесу	Площа прямокутника. Графіки залежності різних величин
13	Електроємність. Конденсатор. Енергія електричного поля	Площа трикутника
14	Індуктивність. Енергія магнітного поля	Площа трикутника

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновки

 

Таким чином, дослідження реалізації міжпредметних зв’язків на уроках фізики та математики дозволяє зробити такі висновки:

Сутність міжпредметних зв’язків полягає у встановленні таких зв’язків між навчальними дисциплінами, які забезпечують формування в учнів загальних синтезованих знань. Систематичне здійснення міжпредметних зв’язків математики і фізики при диференційованому навчанні математики в основній школі дозволяє підвищити якість знань учнів, сприяє формуванню уявлень про методи математичного моделювання, як методу вивчення реальних явищ, надає можливості для розвитку пізнавальних інтересів учнів.

Методична система реалізації міжпредметних зв’язків в загальноосвітній школі повинна відображати в собі взаємозв’язки наступних компонентів: концептуальних засад, суб’єкту, об’єкту, методики та результату реалізації. Методичний інструментарій досліджуваної системи включає в себе засоби, методи та форми, що використовуються для реалізації міжпредметних зв’язків у навчанні фізики, математики. Основним засобом реалізації міжпредметних зв’язків виступають задачі міжпредметного характеру та інтегровані уроки.

Дієвим засобом реалізації міжпредметних зв’язків між фізикою та математикою є розв’язування комплексних синтезованих задач, що інтегрують знання кількох предметів. Задачі фізичного змісту з математики дозволяють наочно розкрити не тільки істотні сторони фізичних законів, але й поглибити знання з математики, допомогти встановити ті невидимі, на перший погляд, зв’язки, які є передумовою узагальненої системи знань. Задачі фізичного змісту можна використовувати на уроках математики, фізики, у позакласній роботі, а також під час проведення нестандартних, зокрема, інтегрованих уроків.

Найефективнішою формою реалізації міжпредметних зв’язків при вивченні математики і фізики в школі є інтегровані уроки. На даних уроках встановлюється взаємозв’язок між дисциплінами по темі, що вивчається. Такі уроки мають на меті реалізацію низки цілей: навчальні – поглибити уявлення про застосування фізичних і математичних законів в різних ситуаціях; розвиваючі – розвивати творчу та розумову діяльність учнів, аналітичні вміння при перенесенні знань з математики в фізику, гнучкості мислення; виховні – формування елементів соціально-особистісної компетентності на основі вміння проектувати і здійснювати алгоритмічну та евристичну діяльність.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Бібліографія

 

1.          ФIЗИКА. 7–9 класи. Навчальна програма для загальноосвітніх навчальних закладів. Програма затверджена Наказом Міністерства освіти і науки України від 07.06.2017 № 804.
2.          ФІЗИКА і АСТРОНОМІЯ.  Навчальні програми для 10-11 класівзакладів загальної середньої освіти (рівень стандарту, профільний рівень) Авторський колектив під керівництвом Ляшенка О. І. Затверджено Міністерством освіти і науки України (наказ № 1539  від  24.11. 2017 р.)
3.          Абрамович В. Теоретичні аспекти міжпредметних зв’язків у шкільній освіті / В. Абрамович // Управління освітою. – 2013. – № 6. – С. 21 – 25.
4.               Капарнік Б. Міжпредметні зв’язки. Сутність поняття / Б. Капарнік // Шкільний світ. – 2012. – № 6. – С. 42 – 49.
5.               Коршак Є.В.   Математичне моделювання під час розв’язування фізичних задач / Є.В. Коршак, Н.М.Коршак // Фізика та астрономія в школі. – 2010. – № 3. – С. 10 – 11.
6.               Мороз О.Д. Інтегроване навчання та міжпредметні зв’язки на уроках художньої культури.  Навчально-методичний посібник для вчителів художньої культури. Балашівський НВК «Колегіум – загальноосвітня школа І – ІІ ступенів». – Березне, 2016. –  61 с.
7.               Нестеренко Ф.П. Математика в шкільному курсі фізики. Посібник для вчителів / Ф.П. Нестеренко –К.,Радянська школа, 1981.-103 с.
8.               Ляхоцька О.Є. Блог учителя фізики. Режим доступу : http://fizikaschool5.blogspot.com/

 

 

 

 

 

 

 

Додатки

 

 

 

 

 

 

Урок №1

Властивості тіл. Фізичні величини. Вимірювання. Засоби вимірювання. Точність вимірювання. Міжнародна система одиниць фізичних величин.

 

Наука починається відтоді, коли починають вимірювати.

Д. I. Менделєєв

 

Мета.

Навчальна. Формувати нові знання про фізичні величини, кратні та  частинні  одиниці, вимірювання фізичних величин, похибки й оцінювання точності вимірювань, ознайомити з вимірювальними приладами, навчити визначати ціну поділки та межі вимірювання вимірювального приладу.

Розвивальна. Розвивати алгоритмічне мислення, пам’ять, увагу.

Виховна. Виховувати працьовитість, акуратність. 

 

Очікувані результати навчально-пізнавальної діяльності учнів
Знаннєвий компонент:	Діяльнісний компонент:	Ціннісний компонент:
наводить прикладифізичних величин; знаєсимволи та одиниціосновнихфізичних величин.	записуєзначенняфізичноївеличини, використовуєпрефікси для утвореннякратних і частинниходиниць; користуєтьсянайпростішимизасобамивимірювання, визначаєцінуподілкишкали; порівнюєзначенняфізичних величин; вимірюєлінійнірозміритіл, об’ємитвердихтіл, рідин і сипкихматеріалів; проводить досліди (індивідуально та в групі) за власним планом або за інструкцією з допомогоювчителя, аналізуєрезультати, робитьвисновки.	усвідомлює як новізнанняспіввідносятьсяізнаявними; висловлюєсудження про роль спостереження і досліду в пізнаннідовкілля

 

Тип уроку. Комбінований.

Прилади та матеріали для роботи з учнями:

•             Для демонстрації: терези, мірний циліндр, штангенциркуль, мікрометр.
•             Задачі до теми.Вимірювання фізичних величин
•             Задачі та завдання підвищеної складності.Вимірювання фізичнихвеличин

Хід уроку

1. Організаційний етап уроку. Актуалізація опорних знань.

Вчитель проводить організацію класу, налаштовує учнів до роботи. 

Актуалізацію опорних знань вчитель проводить через усне опитування. 

1.               Скільки видів атомів відомо науці? Чим пояснюється той факт, що існують мільйони різних речовин? 
2.               Сформулюйте основні положення молекулярно-кінетичної теорії будови речовини. Наведіть приклади, що підтверджують ці положення.
3.               Як можна довести, що між частинками речовини існують проміжки? 
4.               Дайте означення дифузії. Наведіть приклади дифузії. 
5.               Яка будова атома? Ядра атома?

2. Вивчення нового матеріалу.

Фізичні величини. Міжнародна система одиниць. Кратні та частинні одиниці.

 Розповідь вчителя з використанням підручника та наочного матеріалу (таблиці).Світ природних явищ дуже різноманітний, тому, щоб описати їх, потрібно виокремити спільні ознаки явища, або встановити його характерні риси, дати цим ознакам і рисам свої назви, навчитися їх вимірювати, порівнювати між собою, встановлювати між ними зв’язки.

У фізиці характерні ознаки тіл, процесів, явищ називають фізичними величинами.

Фізична величина — це кількісно виражена характеристика тіла або фізичного явища.

Кожна фізична величина має назву, позначається певним символом, виражається числовим значенням, має одиницю вимірювання.

Наприклад, довжина — це фізична величина, яка характеризує протяжність тіл, відстаней. Найчастіше її позначають малою латинською літерою l.

Одиницею довжини є метр. Вимірюють довжину лінійкою.  Зараз у більшості країн світу діє запроваджена в 1960 р. Міжнародна система одиниць, яку називають Система Інтернаціональна (СІ).

До основних одиниць СІ належать:

Довжина — 1м (метр)                               Сила світла — 1 кд (кандела)

Час — 1 с (секунда)                                   Сила струму — 1 А (ампер)

Маса — 1 кг (кілограм)                             Кількість речовини — 1 моль

                           Температура — 1 К (кельвін)

 Для зручності запису великих і малих значень фізичних величин використовують кратні та частинні одиниці. 

 Кратні одиниці— це одиниці, які більші за основні одиниці в 10, 100, 1000 і більше разів.

Частинні одиниці— це одиниці, які менші від основних одиниць у 10, 100, 1000 і більше разів.Наприклад, кілометр (1000 м) — кратна одиниця довжини; сантиметр (0,01 м) — частинна одиниця довжини.

Приставки дляутвореннячасткових ікратниходиниць СІ

 

 

 

 

 

 

 

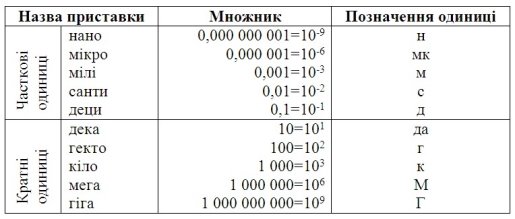
Вимірювання фізичних величин. Прямі та непрямі вимірювання.

Значення фізичних величин одержують шляхом вимірювань. Виміряти фізичну величину означає порівняти її з однорідною величиною, взятою за одиницю.   Значення фізичної величини можна знайти безпосередньо за допомогою вимірювального приладу - це прямі вимірювання.

 Під час непрямого вимірюваннязначення фізичної величини визначають як результат обчислення за певною формулою. Так, щоб визначити площу S прямокутника, спочатку за допомогою лінійки вимірюють (прямі вимірювання) його довжину l і ширину d, а потім обчислюють за формулою S = l d . 

Вимірювальні прилади. Ціна поділки та межі вимірювання вимірювального приладу.

Вимірювання фізичних величин здійснюють спеціальними приладами.

Лінійні виміри (довжина, шлях, висота, відстань).

Лінійка  Рулетка Метр Штангенциркуль

Температура

 

Механічний термометр      Спиртовий термометр         Електронний термометр   

Вимірювальні прилади мають свої характеристики. Найголовніші з них — межі вимірюванняі ціна поділки шкали.

Шкала приладу являє собою сукупність штрихів, поділок і чисел.

Штрихи - це риски, нанесені на шкалі.      Поділки - це відстані між двома найближчими штрихами. Біля деяких штрихів на шкалі стоять числа.

Щоб виміряти фізичну величину потрібно:

•                   З’ясувати з якою точністю ми хочемо проводити  вимірювання            
•                   Підібрати прилад з відповідною шкалою.
•                   Визначити ціну поділки приладу.
•                   Виконати відповідні виміри.

Щоб визначити ціну поділки вимірювального приладу потрібно:

1.               Обрати числові значення проти будь-яких двох найближчих штрихів шкали.
2.               Від більшого значення відняти менше. 
3.               Отримане число розділити на кількість проміжків між обраними штрихами.

Розрахунок ціни поділки лінійки записують так:

 

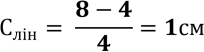
   Нижня межа вимірювання приладу - це найменше значення фізичної величини, яке можна виміряти за допомогою даного приладу. Верхня межа вимірювання приладу - це найбільше значення фізичної величини, яке можна виміряти за допомогою даного приладу.

Для даного термометра: нижня межа вимірювання становить  - 50⁰С, верхня межа вимірювання становить  50⁰С.

Оцінювання точності вимірювання.

 

    Жоден вимірювальний прилад не є абсолютно точним. Причин може бути кілька: неточність виготовлення, зношуваність, температура довкілля, вологість повітря. Тому вимірювальні прилади завжди вносять у результат вимірювання деяку неточність – похибку. Щоб зменшити похибку, вимірювання виконують кілька разів, а потім обчислюють середнє значення результатів вимірювання (знаходять їх середнє арифметичне). Значення виміряної величини А з урахуванням похибки вимірювання записують так:                  А = а ± ∆а,де А вимірювана величина;

а — результат вимірювання;  ∆а — похибка вимірювання. Це означає, що дійсне значення виміряної величини лежить десь поміж значеннями а - ∆а  та а + ∆а

Наприклад, довжина l олівця.

1.               Ціна поділки шкали лінійки — 1 мм. Отже, вважатимемо, що похибка результату вимірювання становить 1 мм ( Δа= 1 мм).
2.               Довжина а олівця, виміряна лінійкою, дорівнює 122 мм (а =122 мм).
3.               Результат вимірювання в цьому випадку слід записати так: l = 122 ± 1 мм. Такий запис означає, що істинне значення довжини олівця перебуває в інтервалі від 121 мм (122 мм – 1 мм) до 123 мм (122 мм + 1 мм).
4.               Вчимося розв’язувати задачі.

Вчитель пропонує учням самостійно  розв’язати задачі, які записані на дошці або на екрані, а потім висвітлює розв’язання.

Задача 1. Подайте в метрах такі значення фізичних величин: 145 мм; 1,5 км;

2 км 32 м.

Розв’язання:

145 мм = 0,145 м 1,5 км = 1500 м

2 км 32 м = 2032 м

Задача 2. Запишіть за допомогою кратних або частинних одиниць такі значення фізичних величин: 0,000 0075 м — діаметр червоних кров’яних тілець; 5 900 000 000 000 м — радіус орбіти планети-карлика Плутона;  6 400 000 м — радіус планети Земля.

Розв’язання:

0,000 0075 м = 7,5 мкм = 7,5 *10^-6 м, 5 900 000 000 000 м = 5,9 Тм = 5,9*10¹² м,  6 400 000 м = 6,4 Мм = 6,4 *10⁶ м

Задача 3. Визначте ціну поділки шкали спідометра, зображеного на рисунку. Визначте швидкість, з якою рухається автомобіль:

Розв’язання:

А)  1. Обираємо числові значення проти будь-яких двох найближчих штрихів шкали:  0 і 40

2.               Від більшого значення віднімаємо менше: 40 – 0 = 40
3.               Отримане число ділимо на кількість проміжків між обраними штрихами:

кількість проміжків – 4. Отже, 40 : 4 = 10. Швидкість автомобіля 70 км/год.

 Б) 

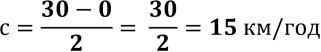
Швидкість автомобіля 135 км/год.

Задача 4.Яку ціну поділки має шкала на вагах, зображених на рисунку?

Укажіть результат зважування. Вкажіть межі вимірювання ваги.

                Розв’язання:

 

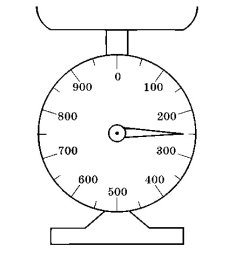
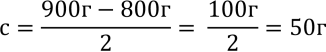
 Результат зважування 250 г.  Межі вимірювання : від 0 г до 1000 г.

 

 

Запитання на закріплення вивченого. 

Закріплення матеріалу вчитель проводить фронтальним опитуванням.

1.               Назвіть відомі вам фізичні величини та одиниці цих величин. Якими приладами їх вимірюють?
2.               Що таке ціна поділки шкали приладу? Як її визначають?
3.               Чому виникають похибки вимірювань? Як записують результати з урахуванням похибки?
4.               Чому виникла потреба введення міжнародної системи одиниць? Які величини вважають основними? Назвіть їх.
5.               Навіщо, на вашу думку, існують еталони одиниць фізичних величин?
6.               У чому різниця між прямими і непрямими вимірюваннями?
7.               Поясніть вираз «Сім разів відміряй — один раз відріж ».

5. Домашнє завдання. Вивчити параграф 4, 5 (Баряхтар) Розв’язати задачі:

Середній рівень.

Задача 1. Визначте ціну поділки термометрів. Яку температуру вони показують? Вкажіть верхню та нижню межу вимірювання приладу.

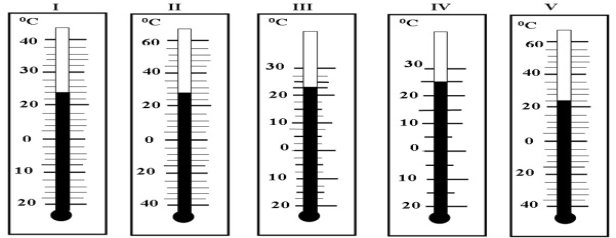
Достатній рівень.

Задача 2. Визначте похибку вимірювання та межі вимірювання термометра, зображених вище.

Задача 3. Визначте ціну поділки кожного з мірних циліндрів. Який об’єм води міститься  у них? Результат запишіть з врахуванням  похибки вимірювання.

 Задача 4. Виразіть  в  системі СІ: 44,05 см; 0,098 дм.

Високий рівень.

Задача 5. Що більше: 0,024 км 24000 см?

Задача 6. Що більше: 36 см чи 0,036 дм? 

 

Урок №2

Об’єм тіла. Лабораторна робота № 2:

"Вимірювання об’єму твердих тіл, рідин  i сипких матеріалів".

Мета.

Освітня. Закріпити знання учнів про фізичну величину — об’єм тіла та методи його вимірювання, похибки та оцінювання точності вимірювань, удосконалити вміння і навички шляхом проведення експерименту щодо вимірювання об’ємів твердих тіл правильної та неправильної форми, води та сипких матеріалів, оцінки точності цих вимірювань поняття об’єму та одиниць його вимірювання. 

Розвиваюча. Розвивати логічне та алгоритмічне мислення.

Виховна. Виховувати працьовитість, акуратність.

Очікувані результати навчально-пізнавальної діяльності учнів
Знаннєвий компонент:	Діяльнісний компонент:	Ціннісний компонент:
наводить прикладифізичних величин; знаєсимволи та одиниціосновнихфізичних величин.	записуєзначенняфізичноївеличини, використовуєпрефікси для утвореннякратних і частинниходиниць; користуєтьсянайпростішимизасобамивимірювання, визначаєцінуподілкишкали; порівнюєзначенняфізичних величин; вимірюєлінійнірозміритіл, об’ємитвердихтіл, рідин і сипкихматеріалів; проводить досліди (індивідуально та в групі) за власним планом або за інструкцією з допомогоювчителя, аналізуєрезультати, робитьвисновки.	усвідомлює як новізнанняспіввідносятьсяізнаявними; висловлюєсудження про роль спостереження і досліду в пізнаннідовкілля

 

 

 

Тип уроку. Урок застосування знань, умінь і навичок. 

Прилади та матеріали для роботи з учнями:

•               Мензурка, тіла правильної та неправильної форми.
•               Для лабораторної роботи: лінійка, мензурка, склянка з водою, тіло неправильної геометричної форми, брусок, горох, шприц, сипкі матеріали (пісок, сіль, мука тощо), ложка. 

План

1.          Актуалізація опорних знань.
2.          Вивчення нового матеріалу.
3.          Виконання лабораторної роботи. 
4.          Домашнє завдання.

Хід уроку

1. Актуалізація опорних знань.

Вчитель викликає до дошки декількох учнів,  які розв’язують домашні задачі.  

В цей час учитель проводить фронтальне   опитування:

1.          Які вимірювання називаються прямими? Навести приклад прямих вимірювань. 
2.          Які вимірювання називаються непрямими? Навести приклад непрямих вимірювань. 
3.          Як можна визначити площу квадрата, прямокутника? 
4.          В яких одиницях вимірюється площа?
5.          Як можна визначити об’єм прямокутного паралелепіпеда? 
6.          В яких одиницях вимірюється об’єм?

2. Вивчення нового матеріалу.

  Вчитель у вигляді бесіди, демонструючи малюнки на екрані пояснює новий матеріал. 

 Ви вмієте визначати об’єм прямокутного паралелепіпеда, а сьогодні навчитеся вимірювати об’єм тіла будь-якої форми.

Пригадуємо разом.

Об’єм — це фізична величина, яка характеризує властивість тіл займати певну частину простору. Об’єм позначають літерою  V. Основна одиниця вимірювання об’єму – 1 м³.  [ V ] = 1 м³.

1 м³ – це об’єм куба зі стороною 1 м.

Крім цих, використовують і інші одиниці вимірювання:

1 м³ = 1000 дм³

1 дм³ = 1000 см³

1 см³ = 1000 мм³ 1 км³ = 1000000000 м³

Пам’ятай!

1 л = 1 дм³ або 1мл=1 см³. 

 

                   Формула об'єму куба

V = а*а*а = a³

Формула об'єму прямокутного паралелепіпеда

 

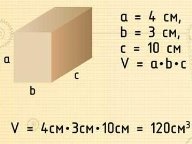
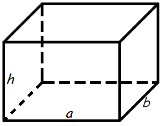           V = a · b · h

 

 

 

 

Визначення об’єму рідини.  Визначити об’єм рідини можна за попередньою формулою. Для цього рідину потрібно вилити в посудину прямокутної форми.

 Так, наприклад, можна визначити об'єм води в акваріумі, в басейні тощо.

Інший спосіб вимірювання об'ємів рідин та сипких матеріалів – використання мірних циліндрів, склянок або колб.

Шкала мірного циліндра рівномірна, тобто відстань між позначками шкали однакова. Шкали склянки і колби – нерівномірні.

Вимірювання об’ємів невеликих тіл неправильної форми.

Об’єм  невеликого тіла можна виміряти за допомогою вимірювального циліндра (мензурки).  Для цього необхідно:

1.          Налити в циліндр стільки води, щоб тіло могло зануритися у неї;
2.          Визначити об’єм води V₁;
3.          Опустити тіло у воду і визначити об’єм тіла і води V₂;
4.          Визначити об’єм тіла: V=V₂-V₁.

 

 

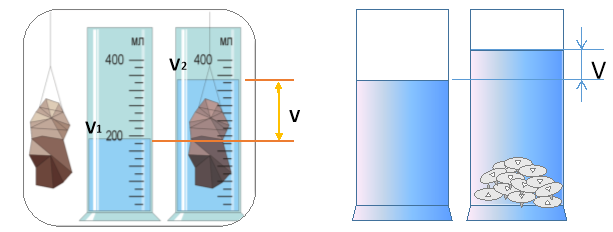
Після пояснення теоретичного матеріалу вчитель пропонує учням виконати лабораторну роботу

3. Виконання лабораторної роботи. Лабораторна робота №2

Вимірювання об’єму твердих тіл, рідин  i сипких матеріалів.

Мета: навчитися виміряти об’єми твердих тіл (правильної і неправильної форм), води та сипких матеріалів.

Обладнання: лінійка, мензурка, склянка з водою, тіло неправильної геометричної форми, брусок, горох, шприц, сипкі матеріали (пісок, сіль, мука тощо), ложка. 

Пригадайте правила «Правила техніки безпеки в кабінеті фізики».

Хід роботи

1.          Визначте ціну поділки шкали лінійки, мензурки, шприца. 
2.          Виміряйте лінійні розміри бруска та обчисліть його об’єм. Результати запишіть у см³ та м³. 
3.          Налийте в мензурку певну кількість води. Виміряйте її об’єм V₁. Опустіть у мензурку з водою тіло неправильної геометричної форми. Виміряйте спільний об’єм води та тіла V₂. Визначте об’єм тіла: V = V₂ -  V₁.
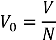4.          Визначте об’єм горошини. Для цього знову налийте воду в мензурку. Виміряйте її об’єм V₁. Опустіть у воду горошини, при цьому точно підрахуйте їх кількість N. Виміряйте спільний об’єм води та горошин V₂. Визначте загальний об’єм горошин: V = V₂ -  V₁.  Визначте об’єм однієї горошини: 
5.          Проведіть вимірювання об’єму повітря. Для цього наберіть у шприц небагато води. Виміряйте її об’єм. Переверніть шприц поршнем донизу. Акуратно опускайте поршень, при цьому у шприц зайде повітря. Визначте його об’єм V₂.
6.          Проведіть вимірювання об’єму сипких матеріалів. Насипте в мензурку піску. Виміряйте його об’єм. Визначте, який об’єм солі міститься в одній чайній (столовій) ложці. Таке саме вимірювання проведіть з цукром (мукою).
7.          Зробіть висновок у якому зазначте:

1.          що саме ви навчилися вимірювати;
2.          які результати отримали;
3.          для чого можуть знадобитися навички, набуті в ході виконання роботи.

Творче завдання

Запропонуйте спосіб вимірювання об’єму власного тіла. Підказка.Можете скористатися ванною з водою і трилітровою банкою.

4. Домашнє завдання.

Вивчити матеріал уроку.

Закінчити виконання лабораторної роботи.

Задача 1. В акваріум довжиною 30 см та шириною 20 см налили води до висоти 25 см. Визначити об’єм води в акваріумі.

Задача 2. Виразіть у кубічних метрах: 7 400 л;  900 дм^3.

Урок №3

Графіки шляху і швидкості при рівномірному прямолінійному русі.

Мета.

Освітня. Навчитися будувати графіки прямолінійного рівномірного руху та по графіках визначати пройдений тілом шлях, швидкість, час руху,  домогтися розуміння функціональної залежності між величинами.

Розвиваюча. Розвивати навички читання графіків, логічне мислення.

Виховна. Виховувати культуру оформлення розв’язків графічних задач та культуру мовлення.

Очікувані результати навчально-пізнавальної діяльності учнів
Знаннєвий компонент:	Діяльнісний компонент:	Ціннісний компонент:
називає види механічного руху; володіє поняттям, формулює визначення фізичної величини (швидкість, переміщення, івміє обрати її одиницю; називає вживані одиниці часу, шляху, швидкості, описує фізичну величину відповідно до узагальнених планів; розуміє відносність руху.	розрізняє види механічного руху за формою траєкторії та характером руху тіла; уміє описати механічний рух графічно й аналітично і провести його аналіз; розраховує пройдений тілом шлях, визначає швидкість руху,  під час розв’язання фізичних задач різного типу; представляє результати вимірювань у вигляді таблиць і графіків; використовує набуті знання для безпечної життєдіяльності.	усвідомлює цінність знань про механічний рух для власного розвитку й безпеки

 

 

 

Тип уроку. Комбінований.

Прилади та матеріали для роботи з учнями:ноутбук, відеопроектор, флеш – анімація «Графік швидкості» 

План

1.               Актуалізація опорних знань
2.               Вивчення нового матеріалу.
3.               Вчимося розв’язувати задачі.
4.               Запитання на закріплення вивченого. 
5.               Домашнє завдання.

Хід уроку

1.Актуалізація опорних знань.

Вчитель перевіряє в учнів  розв’язки  домашніх задач і проводить фронтальне опитування. 

1.               Як визначити шлях, який проходить тіло під час рівномірного руху; позначення шляху, основні та похідні одиниці вимірювання; прилад для вимірювання.
2.               Як визначити час руху тіла; позначення часу, основні та похідні одиниці вимірювання часу; прилад для вимірювання.
3.               Китайський астроном Лося Хун близько 100 року до н.е., вважаючи, що Земля рухається, так обґрунтував своє припущення: “Земля весь час рухається, однак люди не знають цього; вони наче команда на закритому судні, коли воно переміщується, вони цього не помічають”. Чому люди не помічають, що Земля рухається?
4.               Чи можна стверджувати, що траєкторія руху одного й того самого тіла є однаковою для всіх спостерігачів? Відповідь обґрунтуйте.
5.               Потяг повільно їде вздовж перону. Як потрібно рухатися пасажиру в потязі, щоб лишитися нерухомим відносно перону?

2.Вивчення нового матеріалу.

Вчитель починає пояснювати новий матеріал , використовуючи графіки  швидкості та шляху,   виведені на екран.

Графік залежності швидкості прямолінійного рівномірного руху від часу 

v = v(t) .

   Оскільки швидкість руху тіла з плином часу не змінюється графіком швидкості рівномірного руху є пряма паралельна до вісі часу.

За графіком швидкості шлях пройдений тілом за певний проміжок часу чисельно рівний площі прямокутника обмеженого віссю часу, графіком швидкості та прямими, що обмежують проміжок часу руху.

 

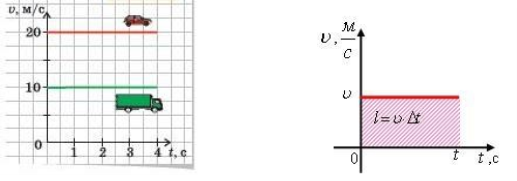
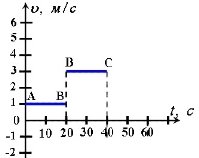Коли тіло на різних ділянках шляху має різну, але постійну швидкість, графік руху буде являти собою сукупність відрізків, кожен з яких відповідатиме значенню швидкості на конкретній ділянці. 

 

 

Графік залежності шляху рівномірного руху від часуl = l(t) .

   З формули для розрахунку шляху рівномірного руху тіла l =vt .  На уроках математики ми використали рівняння  у = kx.

фізика   математика l = vt у = kx l — функція y — функція

 

 Графіком шляху рівномірного руху  є відрізок прямої, який проходить через початок координат і спрямований під кутом до осі часу.

За графіком шляху можна: 

1.               дізнатися, як рухалось тіло; 
2.               знайти шлях, який долало тіло за певний інтервал часу;
3.               3) визначити та порівняти швидкості руху тіл: чим більше швидкість руху тіла, тим більший кут між графіком шляху та віссю часу.

 

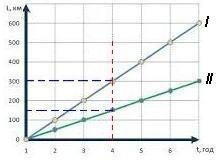І тіло рухається швидше за ІІ: за той самий проміжок часу воно проходить більший шлях.     Чим більший кут нахилу графіка до осі часу - тим більша швидкість тіла.

 

 

3.Вчимося розв’язувати задачі.

Використовуючи графік руху, вчитель разом з учнями розв’язує графічну задачу.

Задача 1. Охарактеризувати рух потяга за поданим графіком руху: 

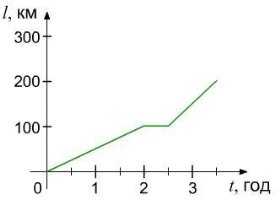
•                   скільки часу рухався потяг;    
•                   яку швидкість мав на різних ділянках  

шляху;                                     

•                   яка середня швидкість на всьому шляху;   
•                   намалювати графік швидкості потягу.

 

 Розв’язання.

       Як бачимо з графіку,  рух потяга можна розбити на 3 ділянки. На першій ділянці потяг рівномірно рухався 2 години, подолавши  100 км. Отже, за формулою швидкості визначимо швидкість на цій ділянці.

   На другій ділянці (з t₁ = 2 год до t₂ = 2,5 год) графік - пряма, паралельна осі часу. Отже, потяг 0,5 год не рухався , його швидкість дорівнювала 0.   На третій ділянці (з t₁ = 2,5 год до t₂ = 3,5 год) графік - похила пряма. Отже, потяг знову рухався рівномірно 1 год зі швидкістю:

    Визначимо середню швидкість потяга за весь час:

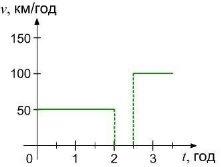   Отже, потяг всього був у русі 3,5 год, проїхав 200 км. Спочатку рухався 2 години рівномірно зі швидкістю 50 км/год, потім 0,5 год стояв, і ще 1 год рухався рівномірно зі швидкістю 100 км/год. А його середня швидкість на всьому шляху 57,14 год. Тепер побудуємо графік швидкості:

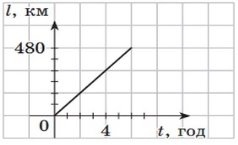Задача 2. За графіком руху вантажного автомобіля визначте: 1) шлях, пройдений автомобілем за 4 год; 2) швидкість руху автомобіля.

 

 

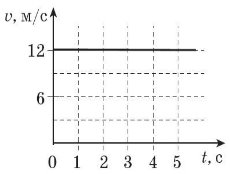Задача 3. За графіком швидкості руху тіла визначте: 1) швидкість руху тіла; 2) шлях, пройдений тіло за 3 с.

 

 

 

Закріплення матеріалу проводиться фронтальним опитуванням.

4.Запитання на закріплення вивченого. 

1.               Який вид має графік залежності шляху від часу в разі рівномірного руху? у разі нерівномірного руху?
2.               Як за графіком залежності шляху від часу для рівномірного руху визначити швидкість руху тіла?
3.               Як за графіками залежності шляху від часу для декількох тіл, які рухаються рівномірно, можна порівняти їхні швидкості?
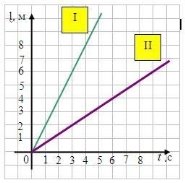4.               Який вид має графік залежності швидкості руху тіла від часу в разі рівномірного руху?
5.               Як за графіком залежності швидкості руху тіла від часу визначити шлях, який пройшло тіло?
6.               Чому чисельно дорівнює шлях пройдений тілом, якщо воно рухалося рівномірно?
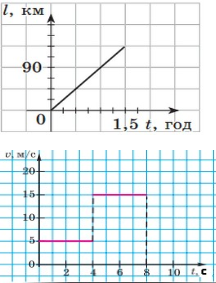7.               Швидкість якоготіла більша  І чи ІІ ? 5.Домашнє завдання.

Підручник:Прочитати § 10 

 

Задача 1. На рисунку зображено графік залежності шляху, який подолав автомобіль, від часу. З якою швидкістю їде автомобіль?

Задача 2.  На рисунку зображено графік залежності швидкості від часу для певного тіла. Побудуйте графік залежності шляху від часу.

 

 

 

 

 

 

 

Урок №4

Прості механізми. Важіль. Умова рівноваги важеля. Блоки.

Мета.

Освітня. Формулювати знання про прості механізми та їх практичну роль в житті   людини, про важіль як один з видів цих механізмів; ввести основні характеристики важеля; ознайомити учнів з правилом моментів. Навчитися розв’язувати задачі на використання умови рівноваги важеля.

Розвиваюча. Розвивати творчі здібності та логічне мислення; показати практичну значущість набутих знань. 

Виховна. Виховувати культуру оформлення задач.

Очікувані результати навчально-пізнавальної діяльності учнів
Знаннєвий компонент:	Діяльнісний компонент:	Ціннісний компонент:
володіє поняттям, формулює визначення фізичної величини (момент сили) і вміє обрати її одиницю; розуміє умову рівноваги важеля, принцип дії простих механізмів; знає різновиди важеля.	застосовує закон збереження енергії та формули  моменту сили під час розв’язування задач різних типів і виконання лабораторних робіт, у практичній діяльності; користується простими механізмами (важіль, нерухомий та рухомий блоки, похила площина); використовує набуті знання для безпечної життєдіяльності.	оцінює ефективність використання простих механізмів; оцінює роль видатних учених у розвитку знань про перетворення енергії

 

 

 

 

Тип уроку. Урок засвоєння нових знань.

Прилади та матеріали для роботи з учнями:проектор, ноутбук.

•                   Демонстрація. Важіль. Будова важеля. Умова рівноваги важеля (штатив, важіль лабораторний, набір важків, динамометр)
•                   Демонстрація. Рухомий блок (рухомий блок, прилад по статиці з магнітними тримачами, магнітна дошка)
•                   Демонстрація. Поліспаст (поліспаст, прилад по статиці з магнітними тримачами, магнітна дошка)
•                   Демонстрація. Похила площина (похила площина, дерев’яний брусок, динамометр)
•                   Демонстрація. Складні механізми (ножиці, домкрат, щипці)
•                   Флеш-анімація.Рівновага важеля
•                   Флеш-анімація.Будівельні роботи 

План

1.               Перевірка домашнього завдання.
2.               Актуалізація опорних знань.
3.               Вивчення нового матеріалу.
4.               Вчимося розв’язувати задачі.
5.               Запитання на закріплення вивченого.
6.               Домашнє завдання.

Хід уроку

1.                 Перевірка домашнього завдання.

Вчитель перевіряє  розв’язки домашніх задач, попередньо вивівши на екран правильні відповіді.

2.                 Актуалізація опорних знань.

Вчитель проводить фронтальне опитування учнів.

•                   Чому ручку дверей розташовують ближче до краю?
•                   Чому маленькі діти їздять на триколісному велосипеді?
•                   Що означає вислів Архімеда «Дайте мені точку опори — і я переверну

Землю» 

•                   Як можна підняти важкий камінь затративши менше сил?

3.                 Вивчення нового матеріалу.

Вчитель розповідає про прості механізми, ілюструючи свою розповідь малюнками, виведеними на екран.

1. Прості механізми.

  Тисячоліття тому назад люди виконували всі види роботи за допомогою сили своїх м'язів. З часом вони винайшли різні прості механізми, щоб полегшити свою працю. Прості механізми — це трудівники зі «стажем роботи» понад 30 століть, проте вони анітрохи не «постаріли», адже зустрічаються на заводах і будівельних майданчиках, у транспортних засобах і побутових приладах.

   Прості механізми - пристрої, призначені для зміни сили. До простих механізмів належать:

•                   важіль(різновид важеля -коловорот);

 

•                   блоки(нерухомий та рухомий);

 

•                   похила площина (різновид похилої площини - гвинтова драбина, гвинт, клин);

 

шестерні. 

2. Важіль

Уже давно відомо, що важке тіло підняти значно легше, якщо просунути під нього міцний стрижень — дошку, лом. 

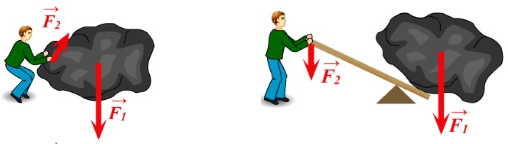
У цьому випадку дошка або лом відіграють роль простого механізму — важеля.

Важіль — це тверде тіло, яке може обертатися навколо нерухомої осі — осі обертання.

 

          

 

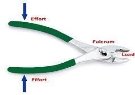
Повністю зрозумів і зумів сформулювати принцип дії важеля  Архімед. Йому належить крилатий вислів « Дайте мені точку опори, і я переверну Землю»

Розглянемо малюнок де є такі позначення : L₁, L₂–плечі сил, F₁,F₂ – сили ,  що діють на плечі важеля

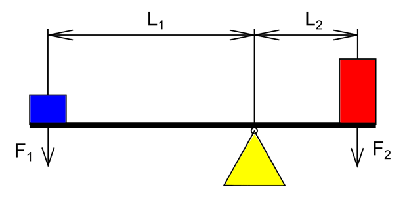
3. Умова рівноваги важеля

   Щоб важіль перебував у рівновазі до довшого плеча прикладається менша сила, а до коротшого - більша.

  Умова рівноваги тіла, яке має вісь обертання: важіль перебуває в рівновазі, коли діючі на нього сили обернено пропорційні плечам цих сил:

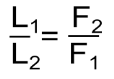У математиці такий вираз    називають пропорція.       

Рівність двох відношень m/k=n/t або m : k = n : t називають пропорцією  

Таким чином, важіль змінює напрям дії сили і дає виграш у силі в  кразів

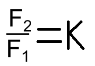
4. Момент сили

  З того часу як Архімед установив умову рівноваги важеля, воно проіснувало в первозданному вигляді майже 1900 років. І лише в 1687 р. французький вчений П. Варіньйоннадав йому більш загальної форми, скориставшись поняттям моменту сили.

   Момент сили фізична величина, що дорівнює добутку сили, яка діє на тіло, на плече цієї сили:  M = Fl .

В СІ момент сили вимірюють в [M] = Н·м, що збігається з розмірністю енергії.    Для важеля, який перебуває у рівновазі під дією двох сил справедливо,  що