Інтегрований урок математика-інформатика в 9 класі

Інтегрований урок математика -інформатика в 9 класі

Тема: Функції. Квадратична функція.

Мета: Закріпити вміння будувати графіки квадратичної функції і за графіком визначати її основні властивості ,  використовуючи властивості квадратичної функції розв'язувати завдання  підвищувати рівень навчальної мотивації з використанням комп'ютерних технологій , розвивати логічне мислення. Виховувати точність та акуратність.

Хід уроку:

         - Сьогодні у нас з вами не зовсім звичайний урок. Ми спробуємо об'єднати знання, отримані на уроках алгебри та інформатики і залучити комп'ютер до вирішення математичних завдань

    - Отже , тема нашого уроку «  Функції. Квадратична функція ». Ми вдосконалимо знання про функції.

I. Повторення відомостей про функції   

 Отже, переходимо до першого етапу нашого уроку . Ви повинні дати відповідь на питання.

1. Що називають функцією? (Змінну y називають функцією від змінної x, якщо кожному значенню змінної х відповідає єдине значення змінної y.

2. Що називають аргументом функції? (Змінна x — незалежна змінна, або аргумент)

3. Що таке область визначення функції . (Множину всіх значень, яких набуває незалежна змінна (аргумент), називають областю визначення функції і позначають так: або .)

4. Що називають областю значень функції? (Множину всіх значень, яких набуває залежна змінна (функція), називають областю значень функції і позначають так: або . )

5. Що називають нулями функції? (Значення аргумента, при якому значення функції дорівнює нулю, називають нулем функції.)

6. Скільки нулів може мати квадратична функція? ( Якщо D>0, два нулі, D=0, то один,   D<0 – жодного)

7. Що називають інтервалами знакосталості?(Кожен із проміжків, на якому функція набуває значень того самого знака, називають проміжком знакосталості функції f.)

8. За яких умов можна стверджувати, що на певному інтервалі функція зростає? спадає?              ( Функція f зростає на певному проміжку, якщо для будь-яких двох значень аргумента з цього проміжку більшому значенню аргумента відповідає більше значення функції.

Функція f спадає на певному проміжку, якщо для будь-яких двох значень аргумента з цього проміжку більшому значенню аргумента відповідає менше значення функції. )

9. Якими перетвореннями графіка функції можна одержати графіки функцій: ; ; ; ; ?

(Графік функції можна одержати з графіка функції за допомогою симетрії відносно осі Oх.

Графік функції  можна одержати з графіка функції за допомогою симетрії відносно осі Oy.

Графік функції , де , можна одержати з графіка функції , розтягнувши графік від осі Oх в а разів () і стиснувши його до осі Oх в разів ().

Графік функції y=f(ax), де , можна одержати з графіка функції , стиснувши графік до осі Oy в а разів () і розтягнувши його від осі Oy в разів ().

Графік функції , де , можна одержати з графіка функції за допомогою паралельного перенесення вздовж осі Oх на m одиниць вправо; графік функції , де , можна одержати з графіка функції за допомогою паралельного перенесення вздовж осі Oх на m одиниць вліво.

 Графік функції , де , можна одержати з графіка функції паралельним перенесенням уздовж осі Ox на m одиниць та вздовж осі Oy на n одиниць.)

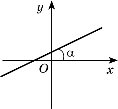
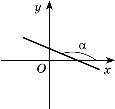
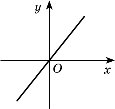
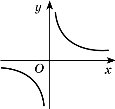
10. Перелічіть відомі вам функції. Який вигляд мають їхні графіки?

Заповни пропуски ...

1 . Функція у = aх² + bx + c , де а , b , c - задані дійсні числа , а ≠ 0 , х - дійсна змінна, називається ... функцією. (Квадратичною)

2. Графік функції у = ах² при будь-якому а ≠ 0 називають ... (Парабола )

3 . Функція у = х² є ... ( зростаючою, спадною) на проміжку х < 0 . (Спадною)

4. Значення х , при яких квадратична функція дорівнює нулю , називають ... функції .

( Нулі)

5 . Точку перетину параболи з віссю симетрії називають ... параболи . ( Вершина)

6 . При а > 0 вітки параболи у = ах² спрямовані .... ( Вгору)

7 . Якщо а <0 і х ≠ 0 , функція у = ах² приймає ... / додатні,від’ємні / значення.  (Від’ємні )

II . Подумай …

Переходимо до другого етапу уроку

Усні завдання:

1 . Знайдіть координати вершини параболи у = х² -4х +4

2 . Знайдіть нулі квадратичної функції у = х² + х - 2

3 . Не виконуючи побудова графіка , визначте , найбільше або найменше значення приймає квадратична функція

у = 2 - 5х- 3х²

4 . За графіком знайдіть значення х , при яких значення функції  у = х² - 5х + 6 додатні, від’ємні, дорівнюють нулю. Знайдіть проміжки зростання та спадання функції .

Письмові завдання:

1. Знайдіть область визначення функції .

2. На параболі знайдіть точки, у яких різниця абсциси і ординати дорівнює –4.

 ІІІ . Робота з програмою Advanced Grapher ...

Третій етап уроку.

 1.Розв’язати  графічно нерівність x²+ 2х - 3 > 5 .

2. Побудуйте графік функції . Використовуючи графік, знайдіть усі значення х, при яких функція набуває від’ємних значень.

3. Розв’яжіть графічно рівняння .

 IV . Розв’яжи ... / робота в групах / .

На цьому етапі уроку учні працюють в групах. Кожній групі пропонується вирішити певне завдання . Після того як всі учні в групі вирішили це завдання , 1 учень виходить і оформлює розв’язокна дошці. Якщо залишається час то учні продовжують вирішувати завдання призначені для інших груп.

 1 група: Знайти значення х , при яких квадратична функція у = 2х² - 5х +3 приймає значення, рівне 1 .

 2 група: Знайдіть координати точок перетину параболи у = х²+ х - 12 з осями координат.

 3 група: Не виконуючи побудови графіка функції у = х² - 4х + 6 , знайти її найбільше або найменше значення .

V. Тест .

Варіант I

1 . З функцій : у = х² + 4 , у = х - 3х² + 1 ,

у = х⁶ -2х + 1 , у = х - 1 ,

у = ( х + 1 )² виберіть квадратичні .

 А ) у = = х² + 4, у х - 3х² + 1;

 Б) у = х² + 4 , у = ( х + 1 )² ;

 В) у = х² + 4 , у = х - 3х² + 1 , у = ( х + 1 )² ;

 Г) у = х⁶ -2х + 1 ;

2 .Розв’яжіть нерівність х² ≤ 121 .

 А ) х < - 11 ;  Б) х ≥ 11 ;

 В) - 11 ≤ х ≤ 11 ;  Г) х ≤ 11 , х > -11 .

3 . Знайдіть координати вершини параболи

у = - 6 ( х - 1 )² .

 А) ( - 6 ; - 1 ) ;  Б) ( 1 , 0) ;

В) ( 0 ; - 1 ) ;  Г) ( 1 , 0) .

4 . Знайдіть координати точок перетину параболи у = - 2х² + 8 з віссю Ох .

А) ( 2 , 0) ; Б) ( 0 , 0) ;

 В) ( 0 , 4) ;  Г) ( 2 , 0) , ( -2 ; 0 ) .

5 . Знайдіть координати точок перетину параболи у = х² + 10х - 11 з віссю ординат.

 А) ( - 11 ; 0 ) ; Б) ( 0 ; - 11 ) ;

В) ( 0 , 0) ; Г) ( - 10 ; - 1).

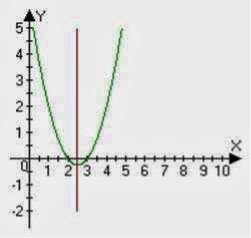
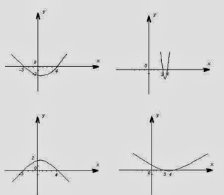
6 . На якому з графіків зображена функція

у = - х² + х + 12 ?

Варіант 2

1 . З функцій у = х² + 3х + 1 , у =х² + 5 ,

у = - х² + 3х , у = ( х - 4 ) ²+ 5 ,
у = х + 3х + 2 , у = х⁴ - 6х виберіть квадратичні .

 А ) у = х² + 3х + 1 , у = х + 3х + 2 ;

 Б) у =х² + 5 , у = х² + 3х + 1 ;
В) у = х² + 3х + 1 , у = - х² + 3х ;

 Г) у = х² + 3х + 1 , у =х²+ 5 , у = - х² + 3х , у = ( х - 4 )² + 5 .

2 . Розв’яжіть нерівність х² ≥ 100 .

 А ) х ≥ 10 ; Б) - 10 ≤ х ;

 В) - 10 < х <10 ; Г) х ≤  - 10 ; х ≥ 10 .

3 . Знайдіть координати вершини параболи y= 2 ( х + 3 )² - 5 .

 А) ( 3 ; -5 ) ; Б) ( 3 , 5) ;

 В) ( -3 ; -5 ) ; Г) ( -3 ; 5 ) .

4 . Знайдіть координати точок перетину параболи у = 3х² - 48 з віссю абсцис.

А) ( 0 , 4) ; Б) ( 4 ; 0 ) , ( -4 ; 0 ) ;

 В) ( 4 ; 0 ) , ( 0, 0 ) ; Г) ( 4 ; 0 ) .

5 . Знайдіть координати точки перетину параболи у = х² +8 х - 9 з віссю Оу .

 А) ( 0 ; -9 ) ; Б) ( 0 , 0) ;

 В) ( -9 ; 0 ) ; Г) (9; -1 ) .

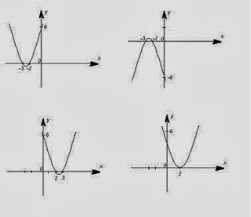6 . На якому ескізі зображено графік функції у = х² + 5х + 6 ?

VI . Підсумок уроку . Д / з .

1. Знайти значення х , при яких квадратична функція у = 2х² - 5х +3 приймає значення, рівне 1.  Перевірити за допомогою програми Advanced Grapher.

2 . Знайдіть координати точок перетину параболи у = х² + х – 12з осями координат.

Перевірити за допомогою програми Advanced Grapher

3 . Не будуючи графік функції у = х² - 4х + 6 , знайти її найбільше або найменше значення.