Презентація "Використання інтеграла для обчислення площ"
Про матеріал
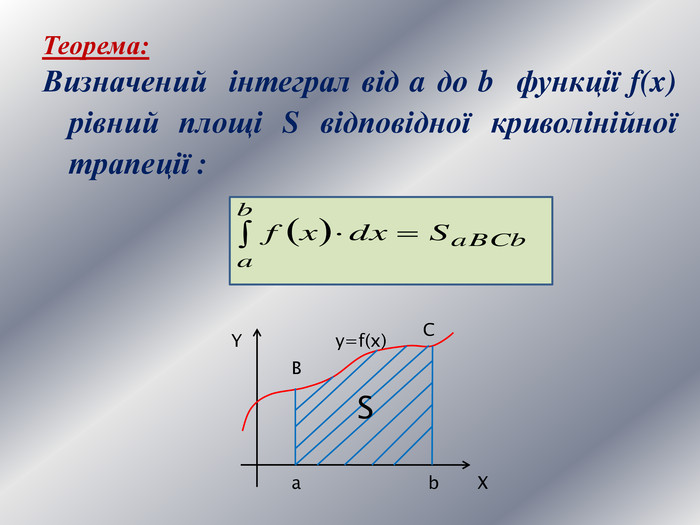
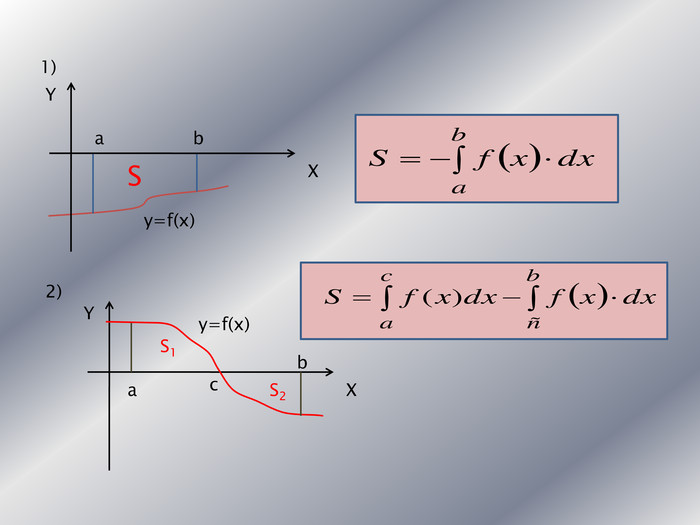
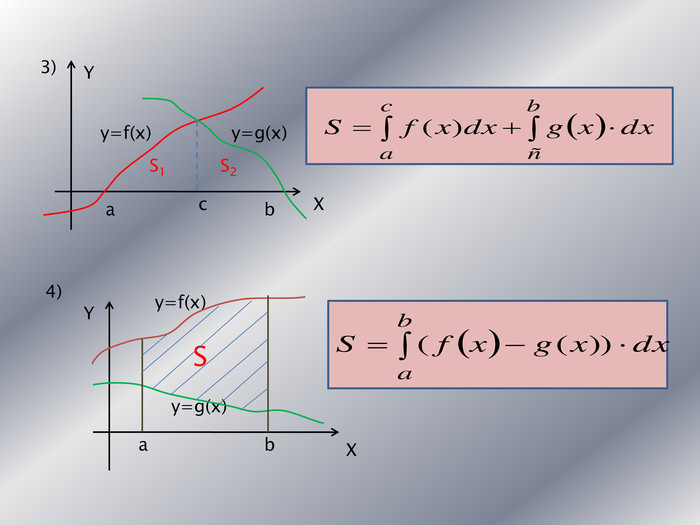
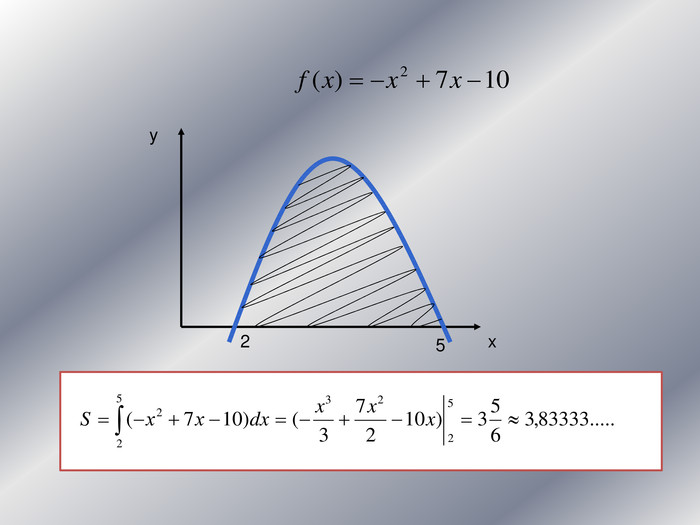
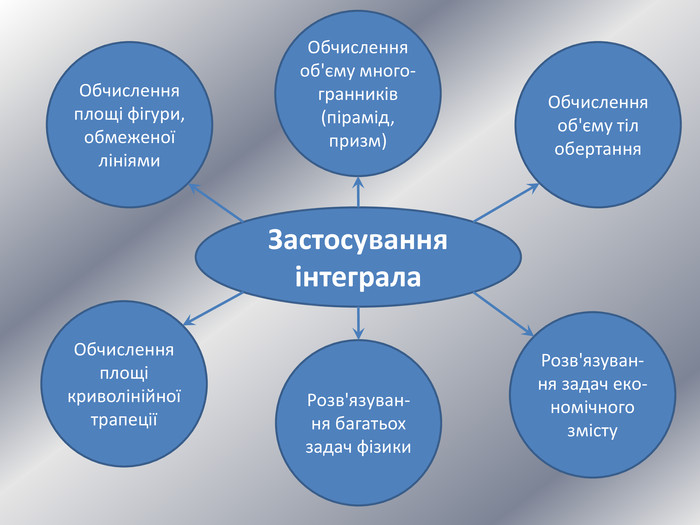
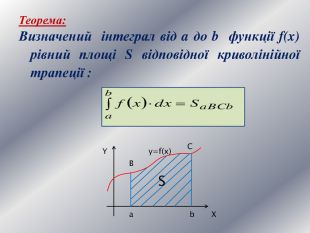
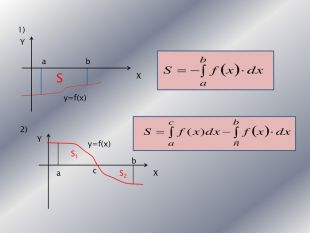
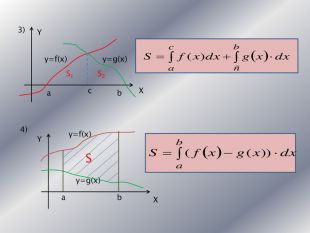
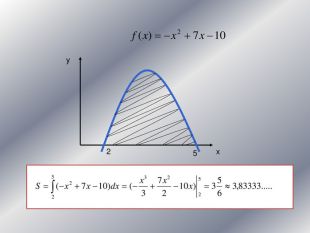
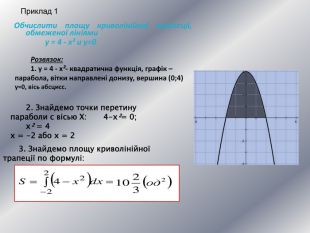
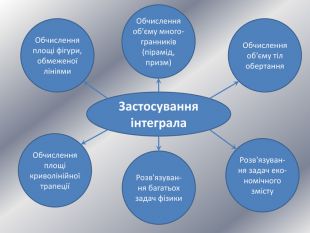
Дану презентацію можна використати для проведення підсумкового уроку по обчисленню площ криволінійних трапецій та площ фігур обмежених лінією.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





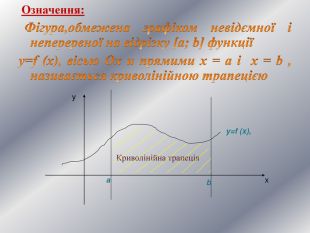
![Означення: Фігура,обмежена графіком невідємної і неперервної на відрізку [a; b] функції y=f (x), вісью Ох и прямими х = а і х = b , називається криволінійною трапецією xyy=f (x),аb. Криволінійна трапеція Означення: Фігура,обмежена графіком невідємної і неперервної на відрізку [a; b] функції y=f (x), вісью Ох и прямими х = а і х = b , називається криволінійною трапецією xyy=f (x),аb. Криволінійна трапеція](/uploads/files/21542/13852/14148_images/5.jpg)