Інтегрований урок: "Об'єм циліндра"

Урок геометрії і спеціальної технології

з професії «Слюсар з ремонту автомобілів Електрогазозварник»

Розробила:

викладач математики

Власенко Юлія Володимирівна

Тема уроку: «Циліндр. Об’єм циліндра»

Мета уроку:

навчальна:  сформувати в учнів знання про циліндр його елементи, навчити обчислювати об’єм циліндра, обґрунтувати значення вивчення теми та використання її в майбутній професійній діяльності;

розвивальна:  розвивати в учнів увагу, мислення, пам’ять, культуру математичного мовлення, вміння працювати самостійно, аналізувати, оцінювати свої дії та дії інших учнів; сприяти розвитку комунікативної, інформаційної, соціальної, полікультурної компетентностей, а також самоосвіти й саморозвитку, продуктивної творчої діяльності;

виховна: виховувати спостережливість, комунікативні вміння, взаємодопомогу і взаємоповагу, навички індивідуальної і колективної роботи; інформаційну культуру учнів, увагу, акуратність у виконанні роботи.

Тип уроку: урок засвоєння нових знань.

Вид уроку: бінарний

Методи навчання: словесний, наочний (демонстрація презентації, технологічних схем, плакатів), практично-орієнтований, проблемний, з елементами ділової гри

Форми навчання: індивідуальна, колективна, фронтальна, самостійна робота учнів, практичні вправи, розв’язування задач.

Міжпредметні зв’язки: спеціальна технологія, матеріалознавство, виробниче навчання, охорона праці, інформатика, фізика, історія.

Дидактичне і  матеріально – технічне забезпечення: картки – завдання, відеозапис, фотографії, слайди, плакати, таблиці, рухома модель поршня автомобіля, комп’ютер, презентація, слайд – шоу.

Девіз уроку:

Ми живемо в геометричний період і

навкруги нас – геометрія

Лє Корбюзьє

Хід уроку

І.Організаційний момент

• Готовність групи до уроку
• Перевірка явки учнів та їх готовності до уроку

ІІ. Актуалізація опорних знань учнів

  1. Які асоціації у вас викликає слово «УРОК»?

Давайте його розкладемо по літерах:

У –успіх; Р – радість; О - обдарованість; К – кмітливість.

Сподіваюсь, що сьогодні на уроці на вас чекає і успіх, і радість. Ви зможете продемонструвати свою обдарованість і кмітливість

2.Перевірка домашнього завдання:

«Для розуміння наступного потрібно розуміння попереднього» - під таким гаслом у нас пройде перевірка домашнього завдання

3. Інтерактивна вправа «Асоціативний кущ»

Із запропонованих геометричних фігур виберіть ті, які є тілами обертання.

ІІІ. Мотивація навчання

Нас об’єднує любов до математики, бажання працювати за обраною професією. Тож приязно подивимося один одному в очі, побажаємо натхнення в нашій роботі.

 Як вам відомо геометрія виникла ще в далекій давнині, коли людям довелося займатись вимірюванням відстаней, обчислювати площі геометричних тіл різноманітної форми і різних розмірів, обчислювати місткість різних споруд, посудин, деталей.

Навколишні предмети ми можемо вивчати по різному.

Наприклад, про училищну будівлю ми можемо сказати, що вона цегляна (або дерев’яна), темно – червона ( або іншого кольору); стовбур берези білий, кабінет світлий, теплий.

Проте вивчаючи геометрію, ми не цікавимося, з якого матеріалу зроблено навколишні предмети, якого вони кольору, в якому вони стані. При вивченні геометрії нас цікавлять форми і розміри предметів.

Як сказав видатний французький архітектор Лє Корбюзьє: «Ми живемо в геометричний період і навкруги нас – геометрія»

І справді, світ, в якому ми живемо, наповнений геометрією будинків і вулиць, творіннями природи й людини. Геометрія є могутнім інструментом пізнання природи і створення техніки. Вона виявляється скрізь, де потрібна найменша точність у визначенні форми і розмірів. Техніку, інженеру, робітнику, архітектору, автослюсарю – всім необхідна геометрична уява. Багатогранники знаходять широке застосування у повсякденному житті, науці і техніці.

Сьогодні ми продовжимо наше знайомство з  багатогранниками, тілами обертання та розглянемо як обчислюється об’єм циліндра

Відкриваємо зошити і записуємо тему сьогоднішнього уроку «Циліндр. Об’єм циліндра»

Якщо озирнутися навколо, то можна побачити багато предметів циліндричної форми. Це і

• предмети побуту,
• продукти харчування,
• канцелярське та хімічне приладдя,
• косметичні товари,
• різноманітні автомобільні деталі тощо.

На практиці часто виникає потреба знати не тільки яку геометричну форму мають деякі предмети, а й знати їх об’єми.

Так іноді на практиці необхідно, наприклад, знайти об'єм пальної суміші в циліндрі автомобіля.

Для початку давайте проведемо розминку і згадаємо основні елементи циліндра.

Тест – розминка

1.Як називається тіло утворене обертанням прямокутника навколо його сторони:

а) кругом    б) конусом,  в) циліндром

2.Якщо прямокутник обертається навколо осі, його сторони описують

а) рівні трикутники

б) рівні круги , які лежать у паралельних площинах

в)рівні квадрати

3.Як називають такий круг ?

а)основою  конуса  б)основою  циліндра   в) колом

4.Сторона АВ, паралельна осі циліндра, описує криву поверхню, яку називають …

а) кругом       б) прямокутником       в) бічною поверхнею циліндра

5.Кожен відрізок бічної поверхні, що дорівнює АВ – це :

а) радіус  круга основи циліндра

б) твірна  циліндра

 в)діагональ прямокутника .

6. Довжина  твірної DС – це :

а) діагональ прямокутника б)висота циліндра  в)радіус круга

ІІІ. Вивчення нового матеріалу

Робота з підручником:

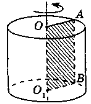
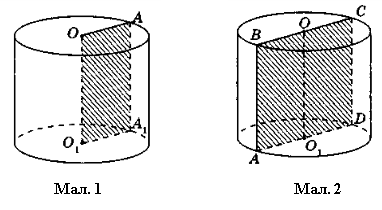
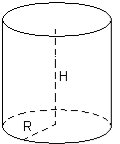
На мал. 1 зображено циліндр, утворений обертанням плос­кого прямокутника ОАВО₁ навколо прямої ОО₁ — осі циліндра.

Сторони ОА і O₁А₁ описують рівні круги, які лежать у па­ралельних площинах і називаються основами циліндра. Радіуси кругів називаються радіусами циліндра.

Сторона АВ описує поверхню, яка називається бічною поверх­нею циліндра. Відрізки бічної поверхні, які паралельні й дорів­нюють АВ, називаються твірними циліндра.

Висотою циліндра називається відрізок, перпендикулярний до основ, циліндра, кінці якого належать основам. Висота цилін­дра дорівнює його твірній.

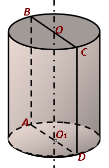
Осьовий переріз циліндра — прямокутник зі сторонами, що дорівнюють висоті циліндра й діаметру його основи. На мал. 2 прямокутник ABCD — осьовий переріз циліндра.

                

 

 

 

 

 

 

Площа поверхні та об'єм циліндра

Поверхня циліндра складається з двох рівних основ і бічної поверхні.

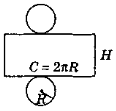
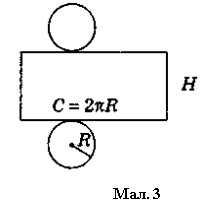
Якщо поверхню циліндра розрізати по колах основ і одній із твірних, а потім розгорнути на площині, то дістанемо розгортку циліндра (мал. 3). Вона складається з

• прямокутника, сторони якого дорівнюють довжині кола основ і  висоті циліндра,
•  двох кругів, що є основами циліндра.

 

 

 

 

 

 

Площею бічної і повної поверхні циліндра називають площу розгортки бічної і повної поверхонь.

Тоді площа бічної поверхні S_бічн і площа повної поверхні S_цил визначаються формулами:

S_бічн = 2πRH,

S_цил = S_бічн + 2S_осн = 2πRH + 2πR² = 2πR(H + R),

де R, H — радіус і висота циліндра відповідно.

Об'єм циліндра дорівнює добутку площі його основи на висоту

V = S_осн ∙ H

Якщо радіус основи циліндра дорівнює R, а висота Н, то його об'єм

V = πR²H

Робота з опорним конспектом:

ЦИЛІНДР

Циліндр
	Прямим круговим циліндром назива­ється тіло, утворене обертанням пря­мокутника навколо його сторони. ОА, О1В — радіуси, АВ — твірна (ви­сота), O1O — вісь
	Площа поверхні циліндра Sцил = Sбічн + 2Sосн, де Sбічн = 2πRH, Sосн = πR2
	Об'єм циліндра V = Sосн ∙ H V = πR2H

 

Учень 1

Тіла обертання широко застосовуються в техніці, особливо в автомобілебудуванні. В цьому можна переконатися, якщо подивитися на форму різних приладів, агрегатів.

Важливу роль в автомобілі відіграють циліндри.

Циліндричні підшипники в автомобілях використовують там, де потрібні підшипники з великою бічною поверхнею і невеликою товщиною (наприклад, у механізмі зчеплення).

У формі циліндра зроблено найважливіші складові частини автомобіля:

• генератор,
• індукційну котушку,
• конденсатори,
• фільтри,
• насоси,
• стартер,
• карданну передачу,
• гідропідсилювач.

Учень 2

Головні робочі частини двигуна — поршні — теж мають форму циліндрів і знаходяться в своєрідних циліндрах.

Поршні служать для передачі зусилля тиску газів, яке виникає внаслідок згоряння робочої суміші, при робочому ході поршня, через поршневий палець і шатун на колінчастий вал.

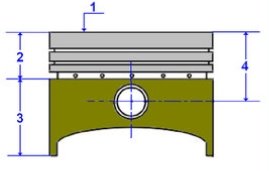Поршень являє собою металевий стакан, днищем повернутий догори. Складається із трьох основних частин:

1.               Днище поршня
2.               Головка поршня
3.               Юбка поршня

 

Днище й ущільнююча частина складають головку поршня.

Учень 3

Днище поршня разом із внутрішньою поверхнею циліндра й головкою блока утворюють камеру згоряння, в якій безпосередньо створюється тиск газів, воно може бути:

• плоским  (у двигунах ЗІЛ-130, ЗМЗ-53),
• випуклим або шатровим (у двигуні автомобіля "Москвич-2140"),
• фасонним або клиновим (у дизелі ЯМЗ - 236),
• з заглибленням  (у дизелі КамАЗ - 740)

 

 

 

 

 

 

Учень 4

 В автомобільних двигунах частіше встановлюють поршні, які виготовляються з алюмінієвого сплаву, так як вони достатньо міцні, легкі, мають високу теплопровідність і добрі антифрикційні властивості.

Викладач:

Про матеріал з якого виготовляють поршні для автомобільних двигунів ви дізналися з уроків матеріалознавства, а про фізичні властивості матеріалу, такі, як міцність, легкість, теплопровідність, антифрикційні властивості з уроків фізики.

Учень 5

У багатоциліндрових двигунах повний об'єм усіх циліндрів виражається в літрах і називається літражем. Таким чином, визначення об'ємів циліндрів є головною характеристикою автомобіля.

Об’єм камери згорання – це об’єм над поршнем, коли він перебуває в верхній мертвій точці (ВМТ).

Робочий об’єм циліндра – це простір, який звільняється при переміщені поршня з ВМТ до нижньої мертвої точки (НМТ).

Сума об’єму камери згорання і робочого об’єму становить повний об’єм циліндра.

Літраж двигуна – це сума робочих об’ємів усіх циліндрів двигуна.

Викладач:

Переглянемо відео фрагмент про принцип роботи циліндра.

 

 

ІV. Закріплення вивченого матеріалу

 Перейдемо до розв’язування задач професійного змісту на обчислення об’єму циліндра.

Розв'язування задач

Задача 1.

Визначити об’єм чотирьохциліндрового двигуна автомобіля ВАЗ 21099, якщо діаметр поршня  82 мм, а хід поршня 71 мм

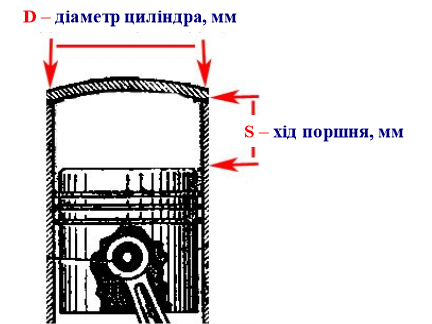Дано:

D = 82 мм = 8,2 см

S = 71 мм = 7,1см

Знайти:

V - ?

 

 

 

 

Робочий об’єм одного циліндра:

V = πD²S / 4

Об’єм чотирьохциліндрового двигуна автомобіля ВАЗ 21099 або літраж двигуна:

V = 4 • (πD²S / 4)

В цій формулі:

D - діаметр поршня двигуна, в міліметрах,

S - хід поршня в міліметрах

Розв’язок: V =  3,14 •  8,2 ²  • 7,1 ≈ 1499 см³ ≈ 1,5 л 

(з фізики відомо, що 1л = 1 дм³ = 0,001 м³ = 1000 см³)

Відповідь: 1,5 л

Задача 2.

У приватному акціонерному об’єднанні "Полтавхіммаш" виготовляють вагон - цистерни моделі 15-1755 для перевезення світлих нафтопродуктів. Яким повинен бути раді­ус основи циліндричної вагон - цистерни висотою   12 м, щоб у неї помістити 86 м³ бензину.

Дано:

Н = 12 м

V = 86 м³

Знайти:

R - ?

 Розв’язок:   Об’єм вагон – цистерни  визначаємо за формулою:

V = πD²H / 4 = πR²H

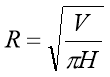
Відповідь: 1,5 м

 

Задача 3.

Ролик підшипника кочен­ня має форму циліндра, висота якого 20 мм, діаметр основи 10 мм. Знайти об'єм та масу шарикопідшипникової сталі, з якого виготовлено ролик.

Дано:

Н = 20 мм = 2см

D = 10 мм = 1см

ρ = 7,9 г/см³

Знайти:

V - ?

 m - ?

Розв’язок:   Об’єм ролика визначаємо за формулою:

V = πD²Н / 4

Масу сталі з якої виготовлено ролик визначаємо за формулою:

m = ρ•V

Користуючись довідковою технічною літературою знаходимо значення густини шарикопідшипникової сталі:

ρ = 7,9 г/см³

V = 3,14 • 1² • 2 / 4 = 1,57 см³

m =7,9 • 1,57 ≈ 12 г

Відповідь: 1,57 см³, 12 г

5. Підведення підсумків уроку. Оцінювання учнів

Викладач: Сьогодні ми повторили означення, основні властивості та формули для обчислення об’єму циліндра, застосували ці знання при розв’язуванні задач прикладного змісту.

І як підсумок до уроку хочу нагадати вам слова мистецтвознавця, доктора філософських наук Олександра Вікторовича Волошина «Математика прекрасна сама по собі, але, коли вона несе цю красу в розвиток цивілізації, це стає пошуком досконалості».

 

Архітектура споруд в місті Полтава, надзвичайно різноманітна і досконала. Але всі вони мають форми геометричних фігур: призм, пірамід і тіл обертання – конуса, циліндра. Подивіться на цю пишність споруд з елементами циліндричних форм.

6.                   Домашнє завдання

Розділ 6, параграф 35 – 36, № 1151 (А), 1210 (Б)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Використана література:

1. Бевз В.Г., Бевз Г.П, Математика 11: рівень стандарту. – К.: Ґенеза, 2011
2. Бондаренко Т. Практичні роботи на уроках математики. – [Електронний ресурс] – Режим доступу: http://klass.ho.ua/index.php?job=100029
3. Кисликов В.С. Будова і експлуатація автомобілів: Підручник. – К.: Либідь, 2005. – 400с.
4. Король Я.А. Формування практичних умінь і навичок на уроках математики / Я. А. Король. – Тернопіль: «Навчальна книга – Богдан», 2000. – 136 с.
5. Роганін О.М. Збірник тренувальних тестових вправ з математики, Х.: Світ дитинства, - 2003
6. Погорєлов О.В. «Геометрія»: Стереометрія, 10-11кл. Київ: Освіта, 2001.