Урок "Многогранники. Тіла обертання."

Узагальнюючий урок по темах: Многогранники. Тіла обертання. Розв’язування задач професійної спрямованостіПідготувала: викладач математики Дашко І. М. 2018 Зеленодольський професійний ліцей

Цілі уроку: Навчальна: повторити пройдений матеріал, систематизувати набутті знання, підкреслити професійну спрямованість і міжпредметні зв’язки по темі, розглянути задачі практичного змісту. Розвиваюча: розвивати в учнів логічне мислення, уміння аналізувати навчальний матеріал, застосовувати набуті знання при виконанні практичних завдань. Виховна: виховувати в учнів працелюбність, інтерес до предмета, влучність міркувань.

Характеристика уроку. Тип уроку; узагальнююче повторення Обладнання; таблиці, макети тіл обертання і многогранниківкартки – завдання професійної спрямованостіметодична розробка « Задачі практичного змісту»методична розробка «Професійна спрямованість у викладанні математики»Форми проведення:групова роботапрезентація практичних робіт (макетів геометричних фігур, задач професійної спрямованості), математична вікторина, доповіді учнів.

Хід уроку 1. Організаційний момент;2. Актуалізація опорних знань та мотивація навчальної діяльності;3. Відповіді на запитання учителя, заповнення карток;4. Доповіді учнів по темі «Геометричні фігури в повсякденному житті»5. Розв'язування задач професійної спрямованості і практичного змісту. Презентація задач професійного змісту групами від різних професій.6. Доповідь учителя про міжпредметні з’язки7. Підведення підсумків уроку і оголошення оцінок; 8. Домашнє завдання.

Робота в групахдомашнє завдання: Зміст:1. Задачі професійного змісту для різних спеціальностей.2. Задачі що демонструють міжпредметні зв'язки.3. Задачі практичного змісту з різних тем геометрії.4. Презентація макетів геометричних фігур.

Задачі професійної спрямованості( для спеціальності електромонтер )1. Кабель складається з чотирьох жил, кожна з яких має діаметр 4мм. Знайти діаметр кабелю, якщо товщина ізоляції 1 мм. Визначити площу поверхні відрізка кабелю довжиною 1м.2. Скільки мідного дроту діаметром 5мм можна прокатати зі злитка об'ємомо0,5м ?

Задачі професійної спрямованості(для спеціальності - електромонтер)3. Термосифонний фільтр являє собою вертикально розміщений циліндр, приєднаний з допомогою трубок до бака трансформатора. Знайти діаметр дна і висоту фільтра,якщо його бічна поверхня s, а об 'єм V°.4. Кабельний колектор прямокутного перерізу має розміри 2300×2400×30000мм2 . Знайти площу поверхні колектора.5. Циліндрична стальна шайба для редуктора-вентиляторатепловоза має такі розміри : зовнішній діаметр 8см,внутрішній діаметр 1,2см, висота шайби 1,5см. Визначити об'єм шайби.

Задачі професійної спрямованості(для спеціальності будівельник).1. При нагріванні тіла розширюються. Тіла збільшують свою первісну довжину. Коефіцієнти лінійного розширення відповідно рівні: цегли – 0,000005, скла – 0,00001, фарфору – 0,000008, цементу – 0,000014. Записати коефіцієнти як степінь.2. Стальний канат діаметром 20 мм накручений в один шар на барабан під'ємноі машини діаметром в 2,5 м. Скількі витків треба накрутити на барабан, щоб кінець каната досягнув глибини шахти в 400м.

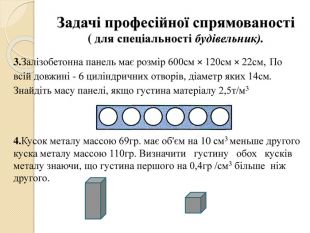
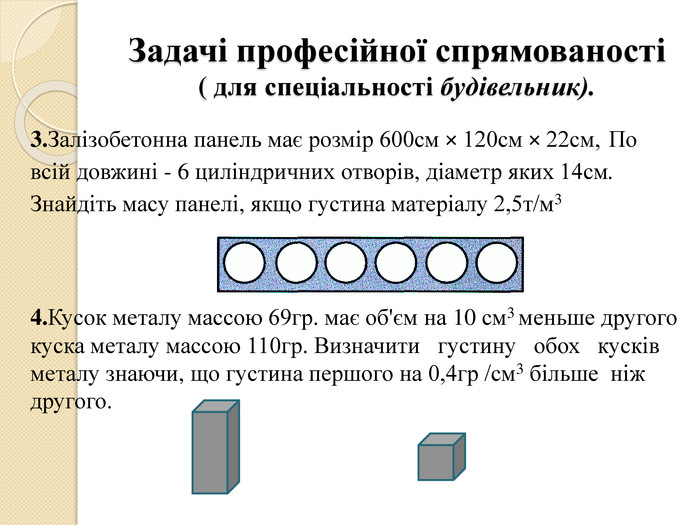
Задачі професійної спрямованості( для спеціальності будівельник).3. Залізобетонна панель має розмір 600см × 120см × 22см, По всій довжині - 6 циліндричних отворів, діаметр яких 14см. Знайдіть масу панелі, якщо густина матеріалу 2,5т/м34. Кусок металу массою 69гр. має об'єм на 10 см3 меньше другого куска металу массою 110гр. Визначити густину обох кусків металу знаючи, що густина першого на 0,4гр /см3 більше ніж другого.

Задачі професійної спрямованості(для спеціальності будівельник) .5. Скільки фарби потрібно для фарбування зовнішній поверхні 100 відер у вигляді конусу. якщо діаметр відер 25см і 30 см, яка становить 27,5см і якщо на 1м2 потрібно 150 г оліфи.6. Скільки покрівельного заліза потрібно для покриття даху вежі, яка має форму шестикутної правильної піраміди зі стороною основи 1,2м, якщо грані нахилені до площини основи під кутом600.

Зв’язок математики з іншими предметами. Доповідь учителя про міжпредметні зв’язки. Демонстрація задач, що ілюструють міжпредметні зв’язки. Розв’язування задач, що показують зв’язок математики з фізикою, кресленням, спецтехнологією електромонтерів, кухарів, будівельників.

Міжпредметні зв'язки. Зв'язок математики зі спецтехнологією кухарів. Задача №1 Визначити місткість каструл і висотою 40см і діаметром основи 35см. V = Sосн × h h = 40см d = 35см

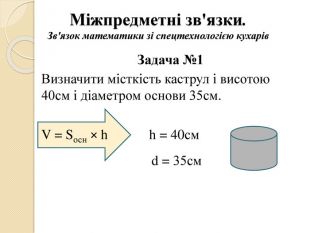
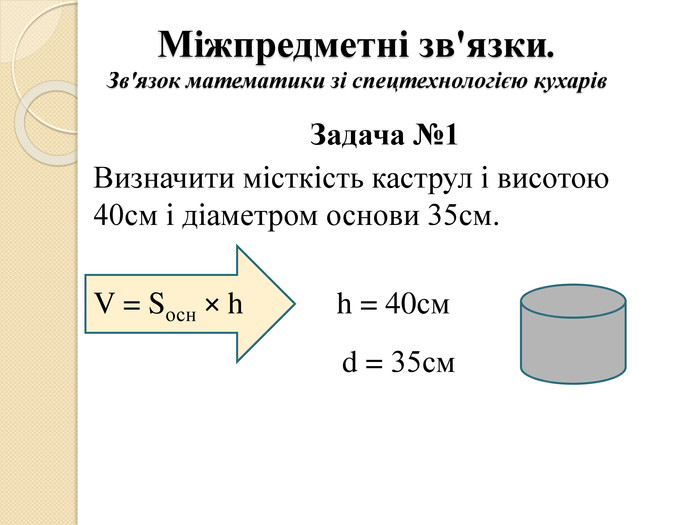
Міжпредметні зв'язки. Зв'язок математики зі спецтехнологією кухарів. Задача №2 Ціна одного кілограма цукерок знизилася на 2,4 гривень, що складає 15% ціни. Скільки коштував кілограм цукерок до зниження?Задача №3 За 5кг крупи і 4кг борошна заплатили 60 гривень. Скільки коштує 1кг борошна і 1кг крупи якщо, 3 кг крупи дорожчі за 2 кг борошна на 14 гривень.

Міжпредметні зв'язки. Зв'язок математики зі спецтехнологією кухарів Задача №4 Контейнер для овочів з (кришкою) має форму прямокутного паралелепіпеда. Сторони його основи відносяться 1 : 2, а площа поверхні дорівнює 108см2. Якими мають бути розміри контейнера, щоб його об'єм був найбільшим? V = a × b ×h h S = Sбіч + 2 × Sосн b Sосн = a × b a

Міжпредметні зв'язки. Зв'язок математики зі спецтехнологією кухарів. Задача №5 Креманка мас форму півсфери діаметром 10см. Чи вмістить вона джем, що зберігався в банці циліндричної форми висотою 10см і діаметром основи 7см ? D1 D2 h Vц = Sосн × h V = 4 × π × 𝑅23/6 Sосн = π × 𝑅12  

Міжпредметні зв'язки. Зв'язок математики з фізикою. Задача №1 Яку силу треба прикласти до вагону масою 8т так, щоб утримати його в рівновазі на рельсовому шляху, нахиленому до обрію під кутом 0,50 ?Задача №2 Знайдіть граничне навантаження, що може витримати латунний дріт, якщо діаметр його поперечного перерізу 2,5мм, а граничне навантаження для латуні при розтягуванні становить 65 кг/мм2

Міжпредметні зв'язки. Зв'язок математики з фізикою. Задача №3 Сталевий дріт діаметром 5 мм мас межу міцності 85кг/мм2 Пpu якій масі вантажу Q дpiт може розірватися?Задача №4 На кожен квадратний сантиметр площі поршня парової машини пара давить із силою 85 Н. Обчислите силу, з якою пара давить на весь поршень діаметром 420 мм.

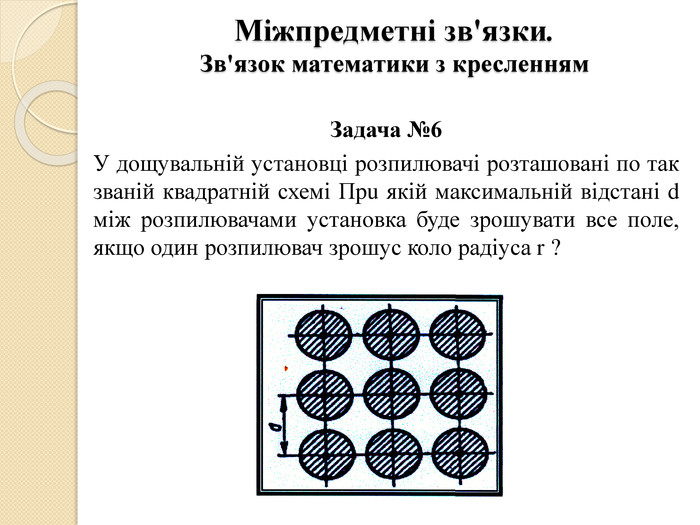
Міжпредметні зв'язки. Зв'язок математики з фізикою. Задача №5 Зовнішня окружність основи заводської труби має довжину 12,56 м, товщина труби 50см. Який тиск чинить труба на основу, якщо її маса 350 т?Задача №6 Двa прожектори розташовані один напроти іншого на прямолінійних паралельних протилежних берегах ріки. Відстань між прожекторами дорівнює 12 км. Прожектори можуть висвітлювати місцевість у радіусі 10 км кожний. Чому дорівнює площа поверхні ріки, освітлюваної цими прожкторами?

Міжпредметні зв'язки. Зв'язок математики з кресленням. Задача №1 Для з'єднання двох дерев'яних брусів в одному з них випиляний фігурний паз ABCDE, в який вставляється відповідним чином випиляний кінець другого бруса. Знайдіть ∟СBA, якщо∟ МАВ = 60°, a ∟BCD = 30°.

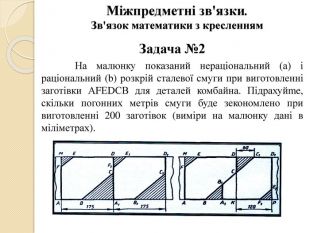
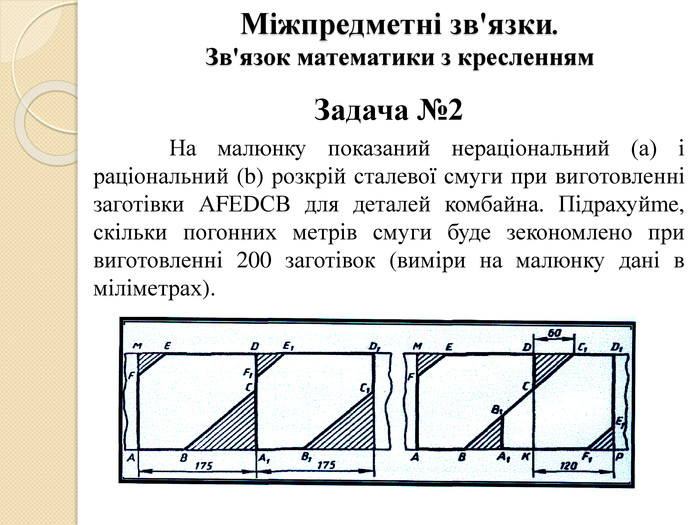
Міжпредметні зв'язки. Зв'язок математики з кресленням. Задача №2 На малюнку показаний нераціональний (а) і раціональний (b) розкрій сталевої смуги при виготовленні заготівки АFЕDСВ для деталей комбайна. Підрахуйme, скільки погонних метрів смуги буде зекономлено при виготовленні 200 заготівок (виміри на малюнку дані в міліметрах).

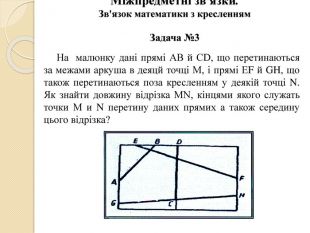
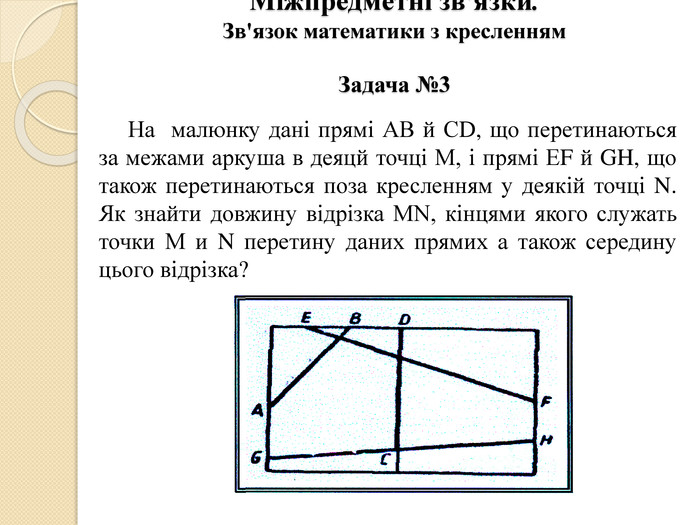
Міжпредметні зв'язки. Зв'язок математики з кресленням. Задача №3 На малюнку дані прямі АВ й СD, що перетинаються за межами аркуша в деяцй точці М, і прямі ЕF й GH, що також перетинаються поза кресленням у деякій точці N. Як знайти довжину відрізка МN, кінцями якого служать точки М и N перетину даних прямих а також середину цього відрізка?

Міжпредметні зв'язки. Зв'язок математики з кресленням. Задача №4 На малюнку зображений навантажувальний кран, стріла ВС якого дорівнює 9м і може мати максимальне відхилення від вертикальної колони АB на кут 64°. Знайдіть радіус дії крана (відстань від вантажу до вертикальної колони).

Міжпредметні зв'язки. Зв'язок математики з кресленням. Задача №5 Підрахуйте радіус малого кола в конструкції рами вікна. зовнішня частина якого має вигляд півкола радіуса R.

Міжпредметні зв'язки. Зв'язок математики з кресленням. Задача №6 У дощувальній установці розпилювачі розташовані по так званій квадратній схемі Пpu якій максимальній відстані d між розпилювачами установка буде зрошувати все поле, якщо один розпилювач зрошус коло радіуса r ?

Розгляд задач практичного змісту. Демонстрація плакатів із задачами практичного змісту (з розв’язками): Задачі практичного змісту по темі «Паралельність прямих»Задачі практичного змісту по темі «Паралельне перенесення»

Задачі практичного змісту по темі: Паралельні прямі. Ознаки паралельності прямих. Задача №1 На плані селища (мал. 1) вулиці АВ й DC паралельні, вулиці АВ й FE становлять кут α, a вулиці EF й AD— кут β. Знайдіть кути, які утворять вулиці AD й АВ, AD й DC. Знайдіть кути, які утворять вулиці AD й AB,AD й DCВідповідь: З малюнка видно, що ∟ DAB = 1800 – (α + β). Так як АВ║DC, то ∟ BAD + ∟ ADС =1800, звідти ∟ ADС = 1800 - ∟ BAD = α + β.

Задачі практичного змісту по темі: Паралельні прямі. Ознаки паралельності прямих. Задача №2 У місті 10 вулиць паралельні одна одній, а 10 інших вулиць перетинають їх під прямим кутом. Яке найменше число поворотів може мати замкнутий маршрут, що проходить через всі перехрестя?Відповідь: Легко привести приклад, коли поворотів 20. Доведемо, що менше 20 поворотів бути не може. Розглянемо 10 вулиць якого-небудь одного напрямку. Якщо маршрут проходить по всіх цих вулицях то на кожній з них є не менш двох поворотів маршруту, і все доведено. Якщо ж найдеться така вулиця по якій маршрут не проходить зовсім, то він повинен проходити по всім десятьох перпендикулярним вулицям. До них, ми можемо застосувати те ж саме міркування.

Задачі практичного змісту по темі: Паралельні прямі. Ознаки паралельності прямих. Задача №3 По одну сторону шосе q перебувають два селища. Потрібно прокласти залізничну лінію L , паралельну шосе й таку щоб сума відстаней від цих селищ до неї буланайменшою. (Залізничну лінію й шосе прийняти за прямі, селища - за точки.)

Відповідь: Проведемо пряму p┴q і спроектуємо точки А и В на пряму р Буквами A1 й В1 позначимо проекції точок А і В на пряму р. Проведемо пряму l║q і відзначимо точку М перетину прямих і р. Якщо М лежить між A1 й В1 то сума відстаней від точок А и В до l дорівнює А1 М + B1 М = А1 В1 (всі розглянуті довжини її відрізків додатні). Якщо точка М лежить на продовженні відрізка А1 В1 то A1 M + B1 M > A1 В1 Таким чином, будь-яка пряма l, паралельна прямій q, яка проходить між точками А і В, є шуканою прямою.

Задачі практичного змісту по темі: Паралельне перенесення. Задача №1 Між пунктами А і В протікає ріка (берега її приймаємо за паралельні прямі а й b). У якому місці ріки варто побудувати міст, щоб шлях від А до В був найкоротшим? (Міст перпендикулярний берегу ріки.)Рішення зображене на малюнку:

Задачі практичного змісту по темі: Паралельне перенесення. Задача №2 Населені пункти А и В розділені двома каналами, кожний з яких має паралельні береги. Де варто побудувати переправу через ці канали, щоб пункти А и В були з'єднані найкоротшими шляхом?Відповідь: Нехай MP й KL — відрізки, перпендикулярні відповідно лініям берегів каналів. Побудуйте образ точки В при паралельному перенесенні, що переводить М в Р, потім образ В при паралельному перенесенні, що переводить К в L. Шлях ACDEFB шуканий.

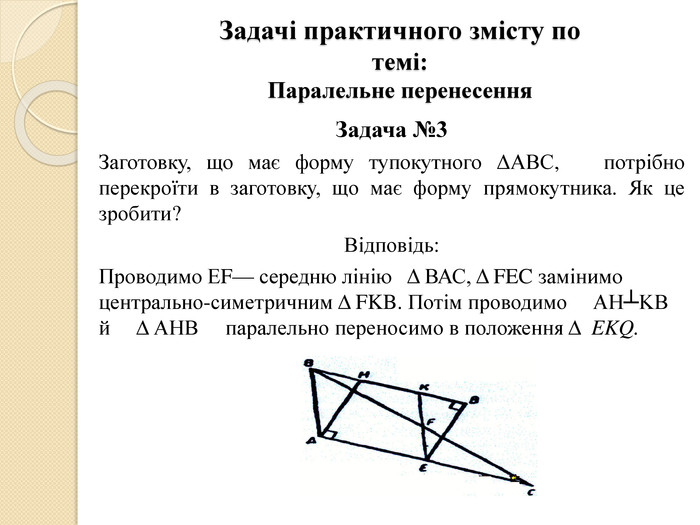
Задачі практичного змісту по темі: Паралельне перенесення. Задача №3 Заготовку, що має форму тупокутного ΔАВС, потрібно перекроїти в заготовку, що має форму прямокутника. Як це зробити?Відповідь: Проводимо ЕF— середню лінію Δ ВАС, Δ FEC замінимо центрально-симетричним Δ FKB. Потім проводимо AH┴KB й Δ АНВ паралельно переносимо в положення Δ EKQ.

Домашнє завдання. Скласти задачу професійної спрямованості по будь-якій з пройдених тем. Скласти задачу, яка б демонструвала зв’язок математики з іншими предметами. Задача. Свинцева труба завтовшки 4 мм має внутрішній діаметр 13 мм. Визначити масу 25 м цієї труби.

Підведення підсумків уроку1. Повторили формули для обчислення площ поверхонь і об'ємів тіл обертання.2. Навчилися застосовувати формули для розрахунку площ поверхонь і об'ємів тіл обертання.3. Закріпили набуті знання при розв'язувані задач професійної спрямованості і практичного змісту.