Методичний посібник "Побудова перерізів многогранників (позиційні задачі)"

Міністерство освіти і науки України

Відділ освіти Ковельської районної державної адміністрації

 

 

 

 

 

 

 

(позиційні задачі)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

О.С.Іванчук – вчитель математики та інформатики загальноосвітньої школи І – ІІІ ступенів с.Поповичі Ковельського району Волинської області.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Посібник містить алгоритми побудови плоских перерізів призми та піраміди за допомогою різних методів.

Для студентів, вчителів загальноосвітніх шкіл та учнів старших класів.

 

 

Розглянуто і схвалено на раді методичного кабінету відділу освіти Ковельської РДА.

Протокол № 2 від 15 березня 2011 року.

 

 

 

ЗМІСТ

 

1.Вступ….………………………………………………...4

2.Основні теоретичні відомості…...…………………………..………………….6

2.1. Використані поняття та терміни ……………..…….6

2.2. Метод слідів ………….……………………………14

2.3. Метод внутрішнього проектування …………..….29

2.4. Метод поділу n – кутної призми (піраміди) на трикутні……………..…………………………………...37

2.5. Метод доповнення  n – кутної призми (піраміди) до трикутної ……………………..…………………………48

2.6 Метод паралельних прямих ……………………….57

3. Висновки та пропозиції………..…………………..66

4. Список використаної літератури..…………..……68        

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. ВСТУП

 

 

Те, що має основою істину,

 потрібно нагадувати,

не боячись здатися набридливим.

М.І.Пирогов

У даному посібнику розглядатимемо декілька способів розв’язування однієї задачі. Адже, психологи встановили, що розв’язування однієї задачі кількома методами приносить більше користі, ніж розв’язування підряд кількох стереотипних задач. Це дає можливість учневі застосовувати весь арсенал математичних знань, виховує гнучкість мислення. Пошук раціонального варіанта лише на перших порах вимагає додаткових витрат часу на розв’язування задачі, у подальшому ж ці витрати з лихвою окупаються.

Як у ряді інших стереометричних задач крім дослідження задачі досліджуватимемо також її розв’язок та доводитимемо разом з тим його істинність.

Найкраще було б записувати доведення, або описувати розв’язування задачі, використовуючи тільки математичні символи відповідної теорії. Тоді кожен крок буде просто перетворенням певних формул за чітко визначеними прийнятими правилами при повному абстрагуванні від змісту формул і правил їх перетворення. Такі доведення називають формальними. Засвоєння їх вимагає значної підготовчої роботи. Доведення в шкільній математиці записуються з використанням і математичних символів і висловів природної мови без фіксації використовуваних правил виведення. Такі доведення називають змістовними, або неформальними. Так будуть подані доведення і в даній розробці.

При розв’язуванні задач на побудову перерізів многогранників, необхідно дотримуватись правил побудови, які використовують у кресленні. Для кращої наочності рисунка останній повинен бути виконаний у такій проекції, яка дає найбільш повне і правильне уявлення про задану фігуру. Для цього видимі лінії креслять суцільними, а невидимі – штриховими. Переріз, про який ідеться в задачі, заштриховують.

Саме завдяки таким задачам наука математика переростає у мистецтво.

              Настоящий ученый, он тоже поэт,

              Вечно жаждущий знать и предвидеть.

              Кто сказал, что в науке поэзии нет?

              Нужно только понять и увидеть!

                                                 (М.Бромлей)                                

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

2.1. Використані поняття та терміни.

Площина називається січною площиною многогранника, якщо по обидві сторони від цієї площини розміщені точки даного многогранника..

Многогранник, сторонами якого є відрізки, по яких січна площина перетинає грані многогранника, називається перерізом многогранника В залежності від взаємного розміщення многогранника і січної площини, переріз може бути трикутником, чотирикутником і т.д., проте число сторін многокутника-перерізу не може перевищувати числа усіх граней даного многогранника. Наприклад, перерізи чотирикутної піраміди площиною можуть мати форму трикутника (рис.1.а), чотирикутника (рис.1.б), п’ятикутника (рис.1.в), причому кожен з цих перерізів може бути представлений у різних варіантах (наприклад, трикутник правильний, рівнобедрений, різносторонній). Така невизначеність трикутника пояснюється тим, що величини кутів і сторін трикутника не інваріантні при паралельному проектуванні. Тому за зображенням не можна визначити вид трикутника. Таке зображення називають необоротним.

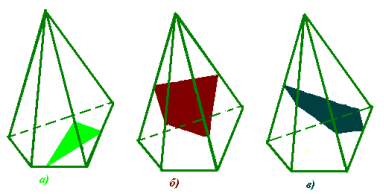
Рис.1

Креслення в такому випадку доповнюють поясненням і називають умовним.

Слід відмітити, що при побудові самих зображень просторових фігур, дотримуючись правил, чітко протиставлялись фігура-оригінал та її зображення у паралельній проекції. Вони по різному позначались, і на кожному кроці доводилось говорити не «висота» або «бісектриса», а «зображення висоти», «проекція бісектриси». На кресленні висота дуже рідко проводилась перпендикулярно до зображення сторони трикутника і т.п.

При побудові перерізів многогранників мова йтиме не про зображення фігур та їх елементів, а про самі фігури, про те , як будується або розміщується в просторі той чи інший елемент фігури-оригіналу. Коли говоритимемо: «Проведемо через точку О пряму, перпендикулярну до прямої АВ», то матимемо на увазі перпендикуляр до прямої АВ у просторовій моделі фігури, незалежно від того, як пряма АВ і перпендикуляр до неї будуть зображені на малюнку. Тобто креслення буде розглядатися лише як ілюстрація, як наочна графічна модель, яка допомагає встановити особливості самої просторової фігури, про яку йде мова у задачі. Міркування, в тому числі в письмових поясненнях, будуть відноситись до самої фігури, а не до її зображення.

У курсі креслення і нарисній геометрії побудову наочного зображення куба, паралелепіпеда, прямої чотирикутної призми частіше виконують у косокутній фронтальній диметричній проекції. У цій проекції коефіцієнт зміни лінійних розмірів натури (оригіналу) на осі Оу становить , а на осях Ох і Оz він дорівнює 1; хОz становить 90°, уОz = хОу = 135° (мал. 40). Таку аксонометричну проекцію називають фронталь­ною диметрією (в літературі її інколи називають ка­бінетною) . За встановленими нормами можна брати 30°, 45°, 60°, тобто  zОу може становити 120°, 135°, 150°.

Означення. Аксонометричною проекцією (або аксо­нометрією) предмета називається його паралельна про­екція на площині, побудована разом з проекцією прямо­кутних координатних осей, в системі яких розміщено зображуваний предмет.

Основні властивості аксонометричних проекцій такі.

1.   Аксонометричною проекцією відрізка  прямої є відрізок  прямої.                                                    

2.  Якщо прямі в просторі паралельні, то їх аксоно­метричні проекції теж паралельні.

3.  Якщо лінії у просторі перетинаються, то і аксоно­метричні проекції цих ліній перетинаються; точка перетину   аксонометричних   проекцій   є   аксонометричною проекцією точки перетину самих ліній у просторі.

4.  Аксонометричні проекції відрізків однієї прямої пропорційні самим відрізкам у просторі.

5.   Якщо пряма в просторі дотикається до якої-не-будь кривої в точці А, то аксонометрична проекція прямої буде дотикатися до аксонометричної проекції кривої у точці А₀, яка є аксонометричною проекцією точки дотику А.

6.  Якщо лінії (прямі, дуги кола або випадкові криві) і сторони кутів лежать у площині, паралельній площині аксонометричних проекцій, то ці лінії і кути проекту­ються на цю площину без зміни.

7. Аксонометричною проекцією кола в загальному ви­падку є еліпс; якщо площина кола паралельна напряму проектування, то аксонометричною проекцією  кола е пряма, і коли площина кола паралельна аксонометрич­ній площині,— коло.

Аксонометричні проекції розрізняють залежно від напряму проектування і величини коефіцієнта зміни розмірів на осях. Якщо напрям проектування перпен­дикулярний до аксонометричної площини, то мають прямокутні аксонометричні проекції. Якщо напрям про­ектування не перпендикулярний до аксонометричної пло­щини, то це косокутні аксонометричні проекції.

      Коефіцієнт зміни показує, в якому відношенні змі­нюється довжина відрізків, паралельних координатним осям в ортогональних проекціях при проектуванні їх на аксонометричну площину. Залежно від співвідношен­ня коефіцієнтів зміни як прямокутні, так і косокутні аксонометричні проекції діляться на ізометричні, ди-метричні і триметричні.

Ізометричні проекції мають по всіх трьох осях однако­ві коефіцієнти зміни. Диметричні проекції мають однако­ві коефіцієнти зміни на двох осях. Триметричні проек­ції по всіх трьох осях мають різні коефіцієнти зміни (загальний випадок аксонометрії). Рекомендується за­стосовувати такі аксонометричні проекції: прямокутні ізометричні, прямокутні диметричні, косокутні диметричні (фронтальні). У кожному конкретному випадку для побудови зображення многогранника слід спочатку прикинути, чи буде відповідна побудова наочною.

По зображенню, отриманому при довільному паралельному проектуванні, оригінал відновити практично не можна, але при розв’язуванні задач шкільного курсу геометрії цього робити і не потрібно.

До проекційних креслень, які виконуються при розв’язуванні задач у середній школі, ставляться слідуючі вимоги:

1. Зображення повинно бути правильним, тобто повинно являти собою фігуру, подібну паралельній проекції оригіналу.
2. Зображення повинно бути по можливості наочним, тобто викликати просторове уявлення про форму оригіналу.
3. Зображення повинно легко виконуватись, тобто правила побудови повинні бути максимально простими. [6,8].

      З поняттям правильного зображення пов’язано також поняття метричної визначеності його. Зображення фігури називається метрично визначеним, якщо по ньому (в принципі) можнавідновити фігуру з точністю до подібності.

Січна площина може бути задана по-різному:

•      трьома точками, які не лежать на одній прямій;
•      прямою і точкою, що їй не належить;
•      двома паралельними прямими;
•      двома прямими, які перетинаються.

Враховуючи основну властивість належності точок і прямих площині (через будь-які дві точки можна провести пряму і до того ж тільки одну) та властивість паралельних прямих (через точку, що не лежить на даній прямій, можна провести на площині не більш як одну пряму, паралельну даній), задача зводиться до побудови січної площини, заданої трьома точками, які не лежать на одній прямій.

У загальному випадку площина перерізу має спільну пряму з площиною кожної грані многогранника. Пряму, по якій січна площина перетинає площину довільної грані многогранника, називають слідом січної площини. Крім задання точок (рис.2.а), які визначають січну площину, необхідно вказати (задати або знайти) проекції цих точок на площину грані (рис.2.б), в якій шукається слід. Тоді всі вершини многогранника і задані точки перерізу будуть заданими, тому дане зображення буде повним [4,120].

 

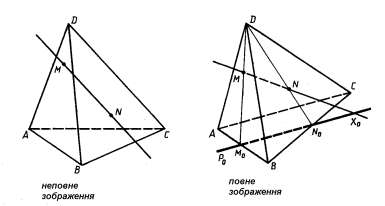
            а)                                             б)

Рис.2.

 

При побудові перерізу призми для зображення проекцій точок використовується принцип паралельного проектування, а при побудові перерізу піраміди – центральне проектування з центром у вершині.

      Незалежно від використовуваного при цьому методу, необхідно розв’язувати дві елементарні задачі:

•      будувати точку перетину прямої (ребра многогранника ) та січної площини;
•      будувати лінію перетину двох площин (січної площини і площини грані).

Побудова перерізу многогранника зводиться до бага­торазового розв'язування задачі на перетин прямої площиною або до розв'язування задачі про перетин двох площин. Розв'язання першої задачі простіше, тому часто для побудови перерізу многогранника визначають вершини перерізу як точки перетину ребер многогран­ника січною площиною. Побудувавши вершини перерізу, сполучають відрізками прямих кожні дві вершини, що належать одній грані многогранника. При цьому сторо­ни перерізу, які належать невидимим граням, будуть невидимі, а які належать видимим граням — видимі.

 

 

 

Умовні позначення:

А, В, С,… - точки

(АВ), m – прямі

[FD] – відрізок

[CK) – промінь

(ABC) – площини

(FK) - пряма FK перетинає пряму АВ в точці N

- точка Р належить прямій АА₁

‌‌‌‌µ║(ABC) – площина µ паралельна площині АВС

 

Побудова точки перетину прямої з площиною

 

Для побудови точки  перетину прямої  з площиною   (сліду прямої  в площині  ) через пряму KL проводимо допоміжну площину, паралельну ребру призми (рис.3.а). така площина буде перетинати бічні грані по прямих КК₁ і LL_1,  паралельних ребру призми, а основу призми – по прямій К₁L₁. Ця пряма і буде тією лінією, по якій площина основи перетинається з допоміжною площиною КК₁L₁L. Якщо (KL) не паралельна (K₁L₁),  то точка М їх перетину і буде шуканою.

Якщо задана піраміда, то в багатьох випадках допоміжну площину доцільно (але не обов’язково) провести через вершину піраміди S (рис.3.б). Така площина буде перетинати грані ABS і CDS по [SK₁] і [SL₁], а площину основи піраміди – по (K₁L₁). Шуканою точкою буде точка М = (KL) ∩ (K₁L₁).

 

 

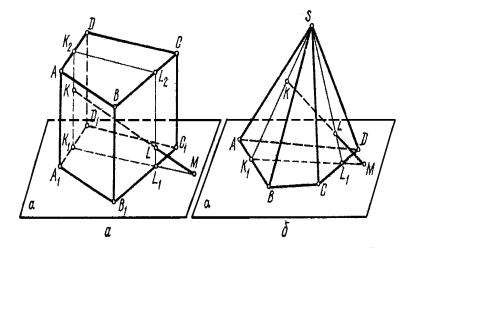
Рис.3.

 

Побудова лінії перетину двох площин

 

 Нехай дано точки А₁,В₁,С₁, які не лежать на одній прямій, та їх проекції А, В, С на площину α. Побудувати лінію перетину площин А₁В₁С₁  та α.

Оскільки дві площини перетинаються по прямій, то для її побудови достатньо знайти дві її точки. Такими точками можуть бути, наприклад, точки перетину прямих А₁В₁ і А₁С₁ з площиною α . побудова зводиться до таких дій:

1) (А₁В₁)∩(АВ)=D;

2) (A₁C₁)∩(AC)=E;

3) (DE)=m(A₁B₁C₁)∩α=m.

(Див.рис.4)

Зауваження . Пряма m називається слідом площини А₁В₁С₁ на площині α . Для наочності зображення можна частину площини А₁В₁С₁ обмежити довільним контуром.

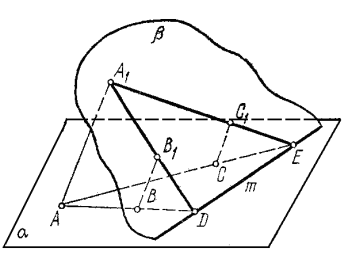
Рис.4.

 

 

 

 

2.2. Метод слідів.

У цьому параграфі розглянемо побудову перерізів методом слідів, який полягає в побудові слідів площини перерізу на гранях даної фігури.

Сліди площини на гранях фігури можна будувати двома способами: а) будувати сліди прямих, що лежать у площині перерізу, а за ними знаходити сліди самої площини; б) будувати третій слід тригранного кута за двома знайденими слідами на площині перерізу.

 

Алгоритм побудови перерізу

 

1. Перевіряємо повноту зображення.
2. Будуємо слід площини перерізу у площині основи.
3. Знаходимо прямі  перетину сліду з площинами  граней   многогранника.
4. Вибудовуємо переріз.

 

На конкретному прикладі покажемо як залежить форма  перерізу від розміщення заданих точок.

 

Приклад

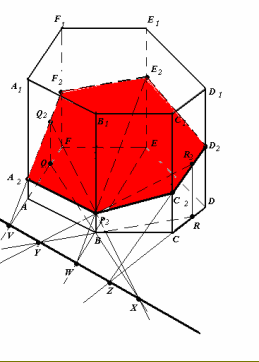
Дано призму ABCDEFA₁B₁C₁D₁E₁F₁. Точки Р₂[BB₁], Q₂ ‌ (АА₁В₁В), R₂   (СС₁D₁D). Побудувати переріз даної призми

площиною (P ₂Q ₂R ₂).

 

 

 

 

 

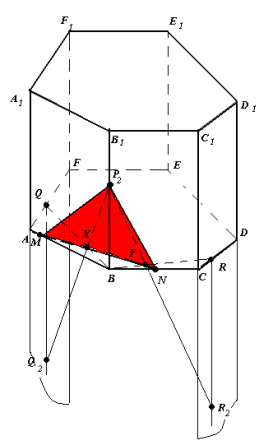
Рис.5

 

1. Q – проекція точки Q₂ на площину основи.

                           R – проекція точки R₂ на площину основи.

      B – проекція точки P₂ на площину основи.

      Зображення повне.

2. (P₂Q₂)∩(BQ)=X, (P₂R₂)∩(BR)=Y.

XY – слід у площині основи.

3. (XY)∩(AB)=M, (XY)∩(BC)=N.
4. Трикутник P₂MN (рис.5) – шуканий переріз .

 

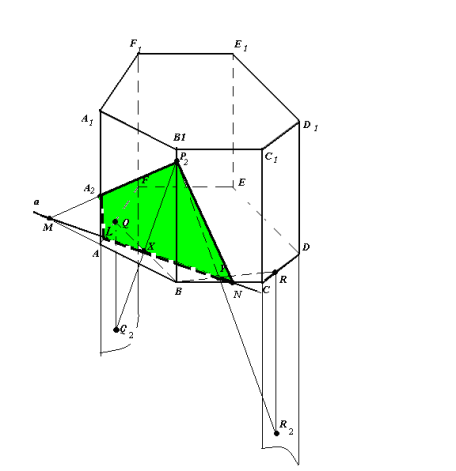
Рис.6

1. Q – проекція точки Q₂ на площину основи.

                  R – проекція точки R₂ на площину основи.

                  B – проекція точки P₂ на площину основи.

                  Зображення повне.

2. (P₂Q₂)∩(BQ)=X, (P₂R₂)∩(BR)=Y.

      XY – слід у площині основи.

3. (XY)∩(AB)=M, (XY)∩(BC)=N, (МР₂)∩(AА₁)=А₂, (XY)∩(AF)=L
4.    Чотирикутник LA₂P₂ N (рис.6) – шуканий переріз.

 

 

 

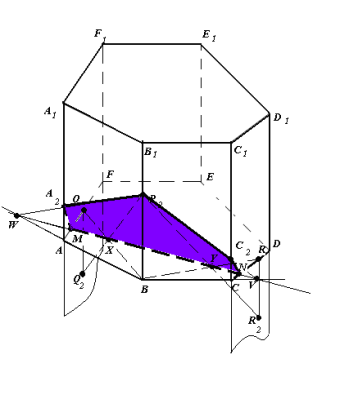
Рис.7

1. Q – проекція точки Q₂ на площину основи.

                           R – проекція точки R₂ на площину основи.

      B – проекція точки P₂ на площину основи.

      Зображення повне.

2. (P₂Q₂)∩(BQ)=X, (P₂R₂)∩(BR)=Y.

XY – слід у площині основи.

3. (XY)∩(AF)=M, (XY)∩(CD)=N,

      (XY)∩(AB)=W, (WP₂)∩(AA₁)=A₂,

      (XY)∩(BC)=V, (VP₂)∩(CC₁)=C₂.

4. П’ятикутник MA₂P₂C₂N (рис.7) – шуканий переріз.

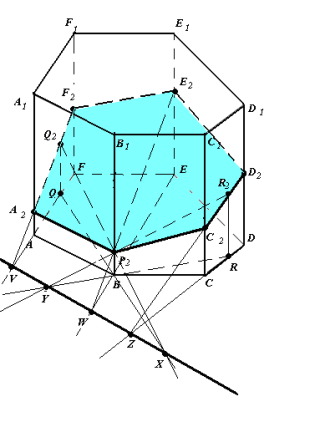
Рис.8

1. Q – проекція точки Q₂ на площину основи.

                           R – проекція точки R₂ на площину основи.

      B – проекція точки P₂ на площину основи.

      Зображення повне.

2. (Q₂P₂)∩(QB)=X, (R₂P₂)∩(RB)=Y.

XY – слід у площині основи.

3. (XY)∩(RC)=Z, (ZR₂)∩(CC₁)=C₂,(ZR₂)∩(DD₁)=D₂

   (XY)∩(QA)=V,(VQ₂)∩(AA₁)=A₂,(VQ₂)∩(FF₁)=F₂

      (XY)∩(EB)=W, (WP₂)∩(EE₁)=E₂.

4. Шестикутник A₂P₂C₂ D₂E₂F₂ (рис.8)– шуканий переріз

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

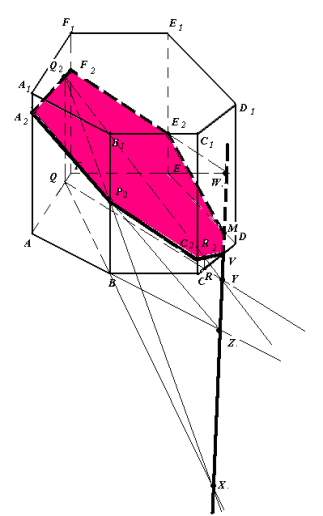
Рис.9

1. Q – проекція точки Q₂ на площину основи.

      R – проекція точки R₂ на пл. основи.

      B – проекція точки P₂ на площину основи.

      Зображення повне.

2. (Q₂P₂)∩(QB)=X, (Q₂R₂)∩(QR)=Y. XY – слід у площині основи.

3.(XY)∩(AB)=Z, (ZP₂)∩(AA₁)=A₂,(CD)∩(XY)=V(XY)∩(ED)=M,(FE)∩(XY)=W,

(A₂Q₂)∩(FF₁)=F₂,(WF₂)∩(EE₁)=E₂.

4.Семикутник A₂P₂C₂ VME₂F₂ (рис.9)– шуканий переріз.

 

 

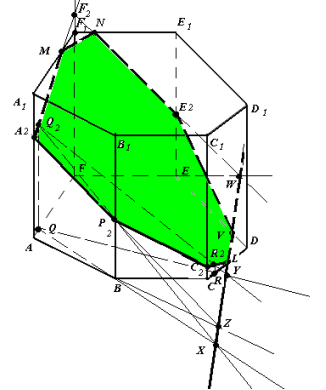
Рис.10

 

1. Q – проекція точки Q₂ на площину основи.

      R – проекція точки R₂ на площину основи.

      B – проекція точки P₂ на площину основи.

      Зображення повне.

2. (Q₂P₂)∩(QB)=X, (Q₂R₂)∩(QR)=Y. XY – слід у площині основи.

3. (XY)∩(AB)=Z, (ZP₂)∩(AA₁)=A₂,(CD)∩(XY)=L,

    (XY)∩(ED)=V,(FE)∩(XY)=W,(A₂,Q₂)∩(A₁,F₁)=M,

    (A₂Q₂)∩(FF₁)=F₂ ,(WF₂)∩(EE₁)=E₂, (WF₂)∩(F₁E₁)=N.

4.Восьмикутник A₂P₂C₂ LVE₂ NM (рис.10) – шуканий переріз.

 

Зауваження. Пряма ХУ — не лише слід, а й носій точок перетину нескінченної сукупності прямих, які належать площині АВС і перетинають основну пло­щину. Це положення є одним з головних під час розв'я­зування задач на побудову перерізів геометричних тіл методом   слідів.[ 3,58]

 

Задача 1.

Bикористовуючи метод слідів , побудувати переріз призми ABCDEFA₁B₁C₁D₁E₁F₁ площиною (Q₂P₂R₂), якщо Q₂ є (AA₁F₁F), P₂ є [BB₁], R₂ є (CC₁D₁D) (рис.11.1).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

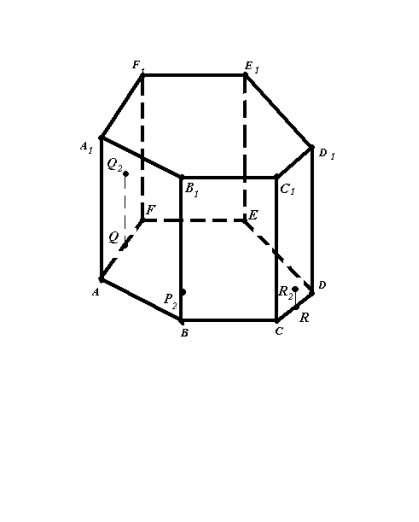
Рис.11.1

1. Q-проекція точки Q₂ на площину основи.

   R-проекція точки R₂ на площину основи.

   B-проекція точки P₂ на площину основи.

   Зображення (рис.11.1) повне.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

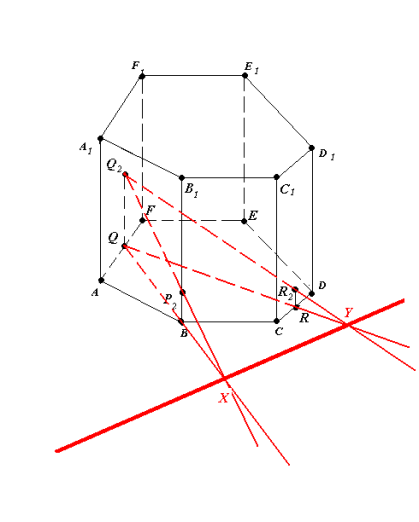
Рис.11.2

 

 

 

 

 

2. (Q₂P₂)∩(QB)=X,  (Q₂R₂)∩(QR)=Y (рис.11..2).

     XY – слід у площині основи.

 

 

 

 

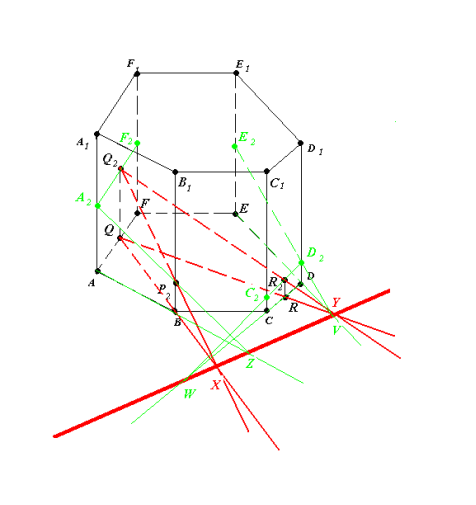Рис.11.3

3. (XY)∩(RC)=W, (WR₂)∩(CC₁)=C_2,

 (AB)∩(XY)=Z, (ZP₂)∩(AA₁)=A₂.

 (WR₂)∩(DD₁)=D_2.

 (ED)∩(XY)=V, (VD₂)∩(EE₁)=E_2, (A₂Q₂)∩(FF₁)=F_2. (рис.11.3)

 

 

 

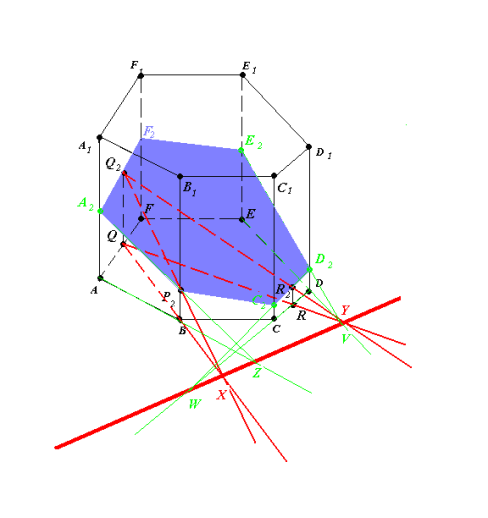
Рис.11.4

 

 

 

 

4. Шестикутник A₂P₂C₂D₂E₂F₂ (рис.11.4) – шуканий переріз.

 

 

Задача 2.

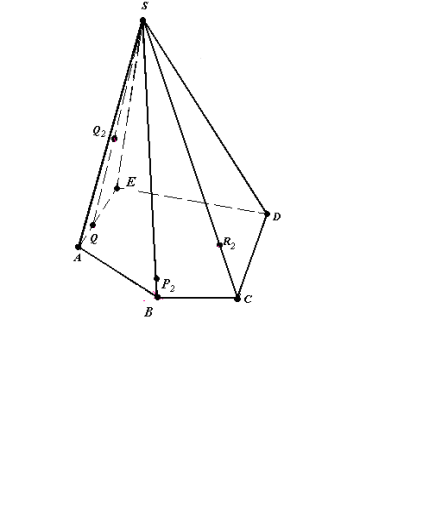
Bикористовуючи метод слідів , побудувати переріз піраміди SABCDE площиною (Q₂P₂R₂), якщо

 Q₂ є (AES), P₂ є [SB], R₂ є [SC] (рис.12.1).

 

 

Р

Рис.12.1

 

 

 

 

1. Q  - проекція Q₂ на площину основи,

       B - проекція P₂ на площину основи,

       C  - проекція R₂ на площину основи.

       Зображення (рис.12.1) повне.

 

 

 

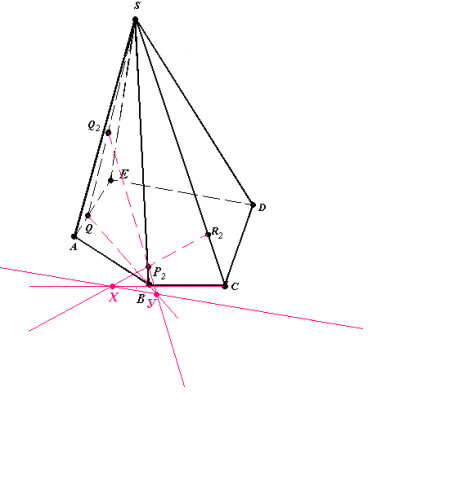
Рис.12.2

 

 

 

 

2.  (CB) ∩ (R₂P₂) = X, (QB) ∩ (Q₂P₂) = Y (рис.12.2).

    XY – слід у площині основи.

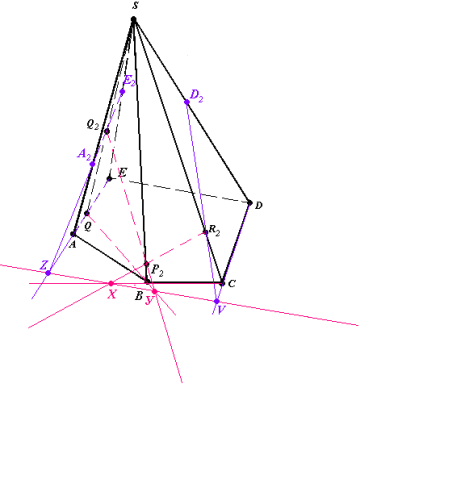
Рис.12.3

 

 

 

 

3. (DC) ∩ (XY) = V, (VR₂) ∩ (DS) = D₂,

       (EA) ∩ (XY) = Z, (ZQ₂) ∩ (AS) = A₂,   (ZQ₂) ∩ (ES) = E₂ (рис.12.3).

 

 

 

 

 

 

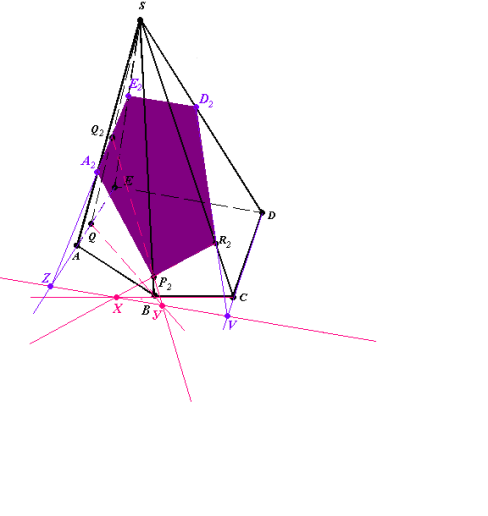
Рис.12.4

 

 

   4.    E₂A₂P₂R₂D₂  (рис.12.4)– шуканий переріз

 

 

 

 

 

Судячи з задач розв'язаних у п.2.2 можна зробити такі висновки.

1.  Задача на побудову точки перетину прямої з пло­щиною є основою методу розв'язування задач на побудо­ву перерізів   многогранників методом слідів.

2.  Побудова сліду (прямої) перетину січної площини (якщо його не задано) з основною площиною є головним етапом  в  розв'язуванні  задачі   на  знаходження  лінії перерізу.

3.  Побудова сліду можлива, якщо задана січна пло­щина не паралельна основній площині і не виходить за межі   аркуша  паперу.[3, 66]

 

 

2.3. Метод внутрішнього проектування.

 

Між точками будь-якої площини, яка не є проектую­чою відносно основної площини, і точками основної площини існує взаємно однозначна відповідність. Це означає, що коли на малюнку задано якусь площину (наприклад, трьома точками), то для кожної точки цієї площини можна побудувати її проекцію, і, навпаки, зна­ючи проекцію точки даної площини, можна побудувати цю точку.

Метод відповідності або внутрішнього проектування грунтується на взаємно однозначній відповідності між точками січної площини та їх проекціями на основну площину.

Розглянемо задачу на побудову точки перетину січ­ної площини з проектуючою прямою, її розв'язання розглянемо для випадку паралельного і центрального проектування.

Зауваження. Метод відповідності зручно за­стосовувати тоді, коли слід січної площини у площині основи многогранника або тіла обертання лежить за межами креслення цих фігур. Незручність цього мето­ду полягає у тому, що велика кількість штрихових лі­ній, які доводиться проводити в процесі розв'язування задачі, викликає помітні труднощі в читанні креслень.[3,76].

 

 

 

Алгоритм побудови перерізу

1.  Вибираємо напрям проектування (для призми –напрям бічного ребра, а для піраміди використовуємо центральне проектування з центром у вершині піраміди). Перевіряємо повноту зображення.
2. Знаходимо точки перетину проекції заданої прямої з діагоналями основи. Будуємо відповідні їм точки у площині перерізу.
3. Знаходимо точки перетину прямих, що належать перерізу з бічними ребрами призми (піраміди).
4. Будуємо переріз.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задача 1.

Bикористовуючи метод внутрішнього проектування , побудувати переріз призми ABCDEFA₁B₁C₁D₁E₁F₁ площиною (Q₂P₂R₂), якщо Q₂ є (AA₁F₁F), P₂ є [BB₁], R₂ є (CC₁D₁D) (рис.13.1).

 

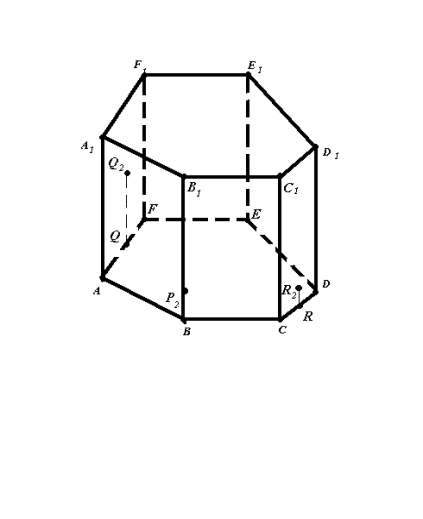
 Рис.13.1

 

 

 

 

1. Q-проекція точки Q₂ на площину основи.

      R-проекція точки R₂ на площину основи.

      B-проекція точки P₂ на площину основи.

      Зображення (рис.13.1) повне.

 

 

 

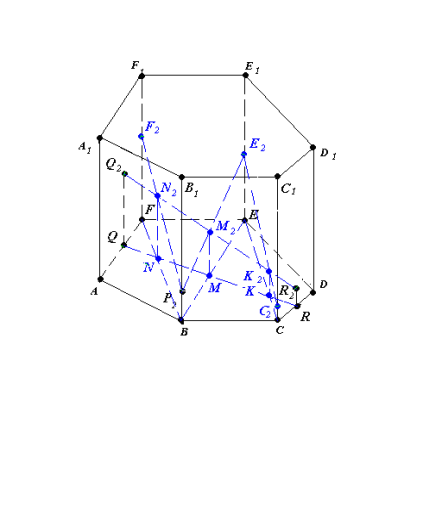
Рис.13.2

 

 

 

1. Як показано на рис.13.2

      (QR)∩(BF)=N, (QR)∩(BE)=M,

      (QR)∩(EC)=K.

     Проводимо через точку N пряму n, паралельну QQ_2,

                          через точку M пряму m, паралельну QQ_2,

                          через точку K пряму k, паралельну QQ_2,  

         n∩(Q₂R₂)=N_2,  m∩(Q₂R₂)=M_2, k∩(Q₂R₂)=K_2.

2. (P₂N₂)∩(FF₁)=F_2,  (P₂M₂)∩(EE₁)=E_2, (E₂K₂)∩(CC₁)=C_2,

 

 

 

 

 

 

 

 

 

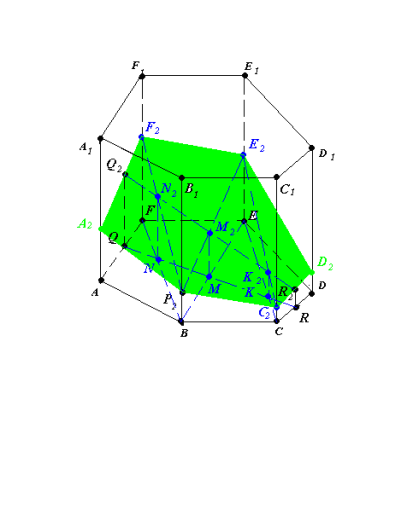
Рис.13.3

 

 

 

      (F₂Q₂)∩(AA₁)=A_2,  (C₂R₂)∩(DD₁)=D₂ (рис.13..3)_,

 

3. A₂P₂C₂D₂E₂F₂ – шуканий переріз.

 

 

 

 

 

 

 

Задача 2.

Bикористовуючи метод внутрішнього проектування , побудувати переріз піраміди SABCDE площиною (Q₂P₂R₂), якщо

 Q₂ є (AES), P₂ є [SB], R₂ є [SC](рис.14.1)

 

 

 

 

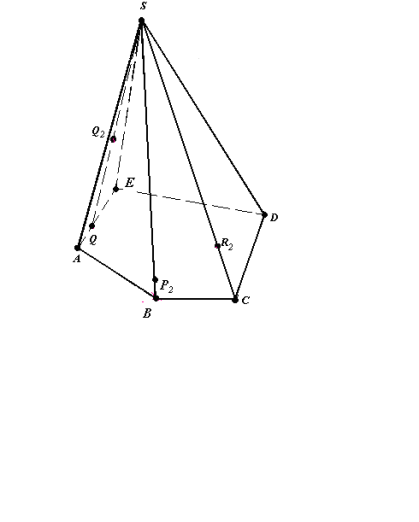
Рис.14.1

 

 

 

1. Q-проекція точки Q₂ на площину основи.

      С-проекція точки R₂ на площину основи.

      B-проекція точки P₂ на площину основи.

      Зображення (рис.14.1) повне.

 

 

 

 

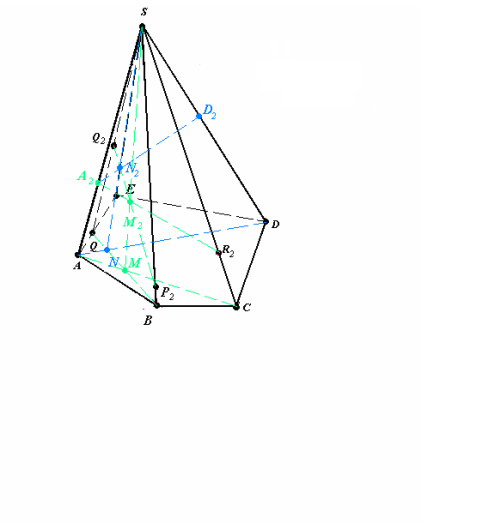                                            Рис.14.2

 

 

 

 

2. (QB)∩(AC)=M, (MS)∩(Q₂P₂)=M₂, (QB)∩(AD)=N, (NS)∩(Q₂P₂)=N₂.
3. (R₂M₂))∩(AS)=A₂, (A₂N₂)∩(DS)=D₂ (рис.14.2),

 

 

 

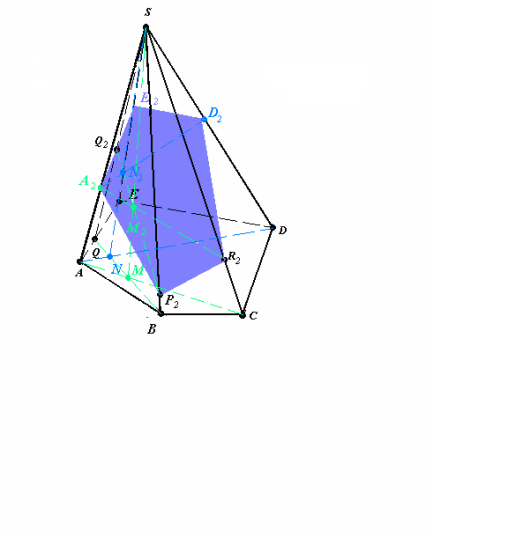
Рис.14. 3

 

 

 

                          (A₂Q₂)∩(ES)=E₂ (рис.14.3)

 

4. A₂P₂R₂D₂E₂- шуканий переріз.

 

 

 

 

 

2.4. Метод поділу n – кутної призми (піраміди) на трикутні.

 

Алгоритм побудови перерізу

1.  Перевіряємо повноту зображення.
2. З даної n – кутної призми (піраміди) виділяємо ту трикутну, на ребрах якої лежать точки, що визначають площину перерізу. Будуємо переріз цієї призми (піраміди).
3. Будуємо перерізи інших трикутних призм (пірамід), які мають спільні частини з даним многогранником.
4. Визначаємо площину шуканого перерізу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задача 1.

Bикористовуючи метод поділу п – кутної призми на трикутні , побудувати переріз призми ABCDEFA₁B₁C₁D₁E₁F₁ площиною (Q₂P₂R₂), якщо Q₂ є (AA₁F₁F), P₂ є [BB₁], R₂ є є(CC₁D₁D) (рис.15.1).

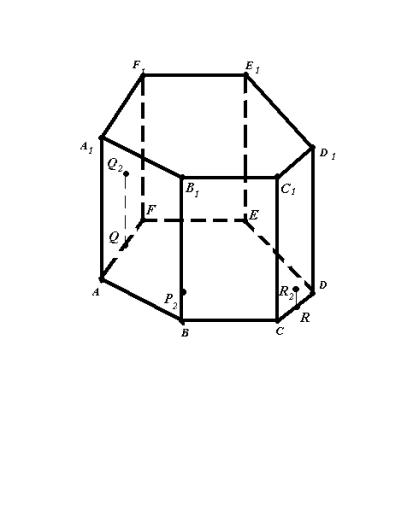Рис.15.1

 

 

 

1. Q-проекція точки Q₂ на площину основи.

      R-проекція точки R₂ на площину основи.

      B-проекція точки P₂ на площину основи.

      Зображення (рис.15.1) повне.

 

 

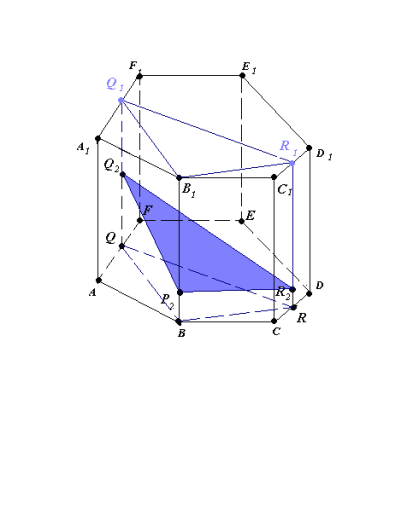
Рис.15.2

 

 

 

 

 

2. P₂ Q₂R₂ – переріз призми BQRB₁Q₁R₁ (рис.15.2).

 

 

 

 

 

 

 

 

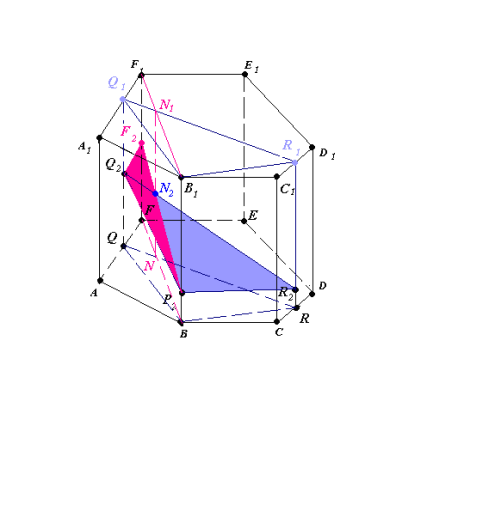
Рис.15.3

 

 

 

 

 

3. (FF₁B₁B)∩(QQ₁R₁R)=NN₁, (NN₁)∩(Q₂R₂)=N₂, (P₂N₂)∩(FF₁)=F₂  (рис.15.3).

 

 

 

 

 

 

 

 

 

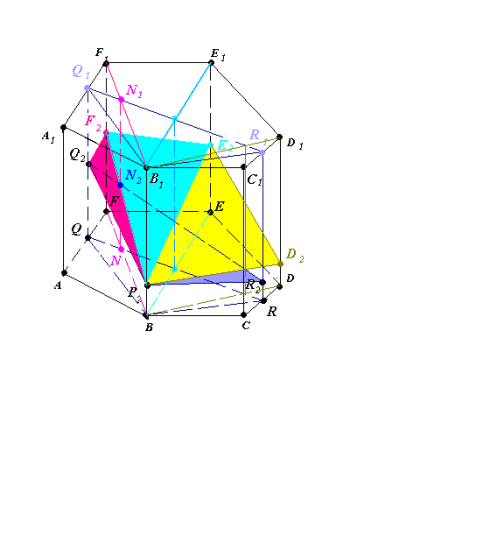
Рис.15.4

 

 

 

 

Аналогічно п.2-3. P₂Q₂F₂-переріз призми BQFB₁Q₁F₁,

                     P₂F₂E₂-переріз призми BFEB₁F₁E₁,

                     P₂E₂D₂-переріз призми BEDB₁E₁D₁.

                               Див.рис.15.4.

 

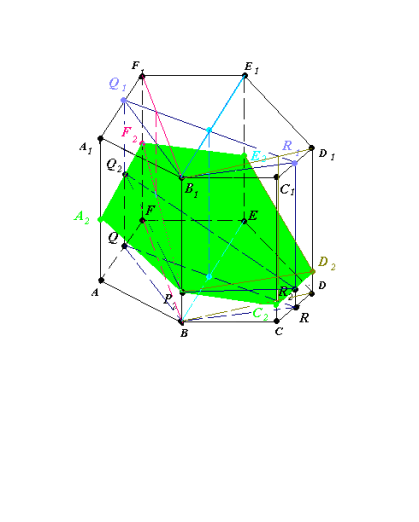
Рис.15.5

 

 

 

 

(D₂R₂)∩(CC₁)=C_2,  (F₂Q₂)∩(AA₁)=A_2, (рис.15.5).

4. A₂P₂C₂D₂E₂F₂ – шуканий переріз._,

 

 

 

 

 

 

 

Задача 2

Bикористовуючи метод поділу п – кутної піраміди  на трикутні , побудувати переріз піраміди SABCDE площиною (Q₂P₂R₂), якщо Q₂ є (AES), P₂ є [SB], R₂ є [SC]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис.16.1

 

 

1. Q-проекція точки Q₂ на площину основи.

      С-проекція точки R₂ на площину основи.

      B-проекція точки P₂ на площину основи.

      Зображення (рис.16.1) повне.

 

 

 

 

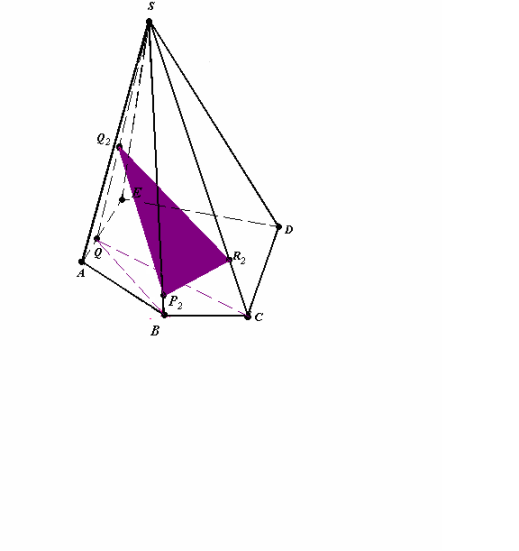Рис.16.2

 

 

 

 

2. (P₂Q₂R₂) – переріз піраміди SBQC (рис.16.2).

 

 

 

 

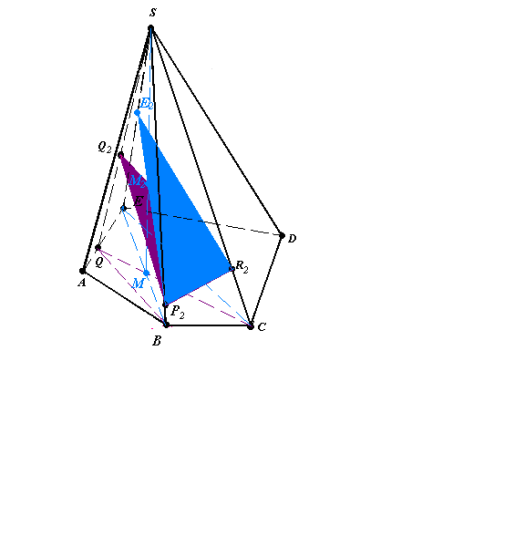
Рис.16.3

 

 

 

                       (BЕS)∩(CQS)=(MS),

                       (MS)∩(Q₂R₂)=M₂, (P₂M₂)∩(ЕS)=E₂(рис.16.3). 

 

 

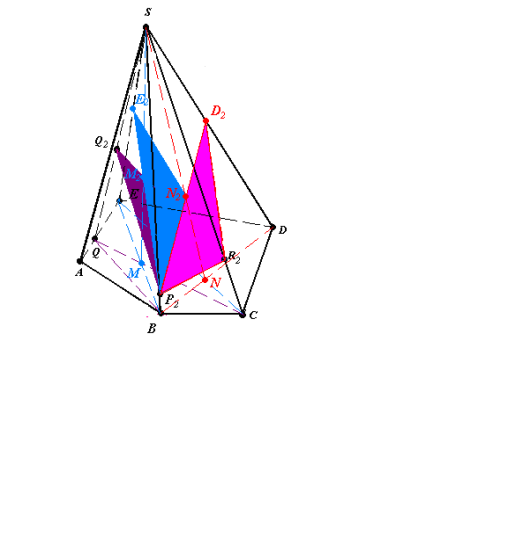
Рис.16.4

 

 

 

Аналогічно п.2. (P₂D₂R₂) – переріз SBDC (рис.16.4), _.

 

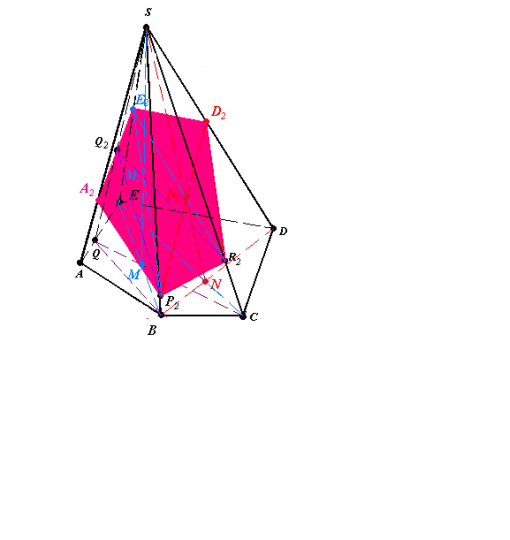
Рис.16. 5

 

 

 

 

                  (E₂Q₂)∩(AS)=A₂ (рис.16.5).

 

              3. A₂P₂R₂D₂E₂ – шуканий переріз.

 

 

 

2.5. Метод доповнення n – кутної призми (піраміди) до трикутної.

 

Алгоритм побудови перерізу

1.  Перевіряємо повноту зображення.
2. Задану призму (піраміду) добудовуємо до трикутної.
3. Будуємо її  переріз.
4. Шуканий переріз дістаємо як частину перерізу трикутної призми (піраміди) .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задача 1.

Bикористовуючи метод доповнення  п – кутної призми до  трикутної , побудувати переріз призми ABCDEFA₁B₁C₁D₁E₁F₁ площиною (Q₂P₂R₂), якщо Q₂ є (AA₁F₁F), P₂ є [BB₁],

R₂ є (CC₁D₁D) (рис.17.1).

 

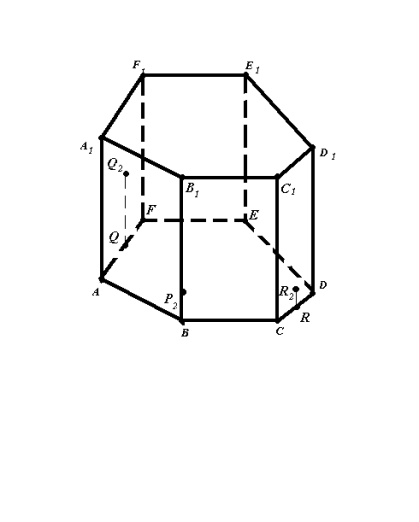
Рис.17.1

 

1. Q  - проекція Q₂ на площину основи,

       B - проекція P₂ на площину основи,

       R - проекція R₂ на площину основи.

       Зображення (рис.17.1) повне.

 

 

 

 

 

 

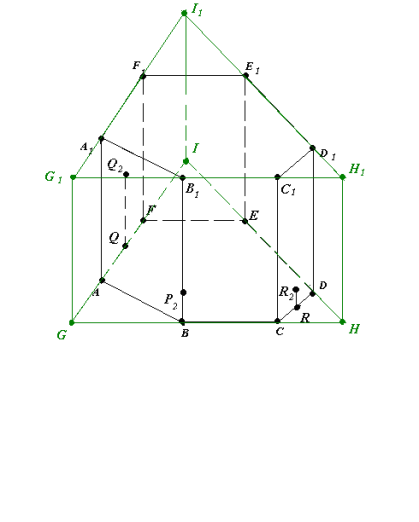
Рис.17.2

 

 

 

 

2. GHIG₁H₁I₁ – доповнена трикутна призма,

               причому Q₂ є (GG₁I₁I), P₂ є (GG₁H₁H) (рис.17. 2).

 

 

 

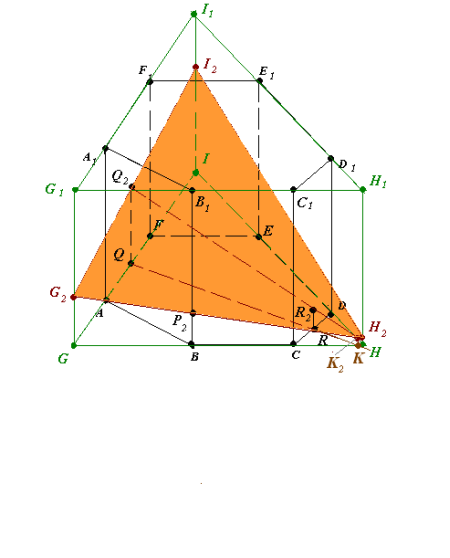
Рис.17.3

 

 

 

3.  (QR)∩(GH) = K (рис.17.3).

       Через точку К проводимо пряму k║(HH₁).

        (Q₂R₂)∩k =K₂

               (P₂K₂)∩(HH₁) = H₂, (P₂K₂)∩(GG₁) = G₂, (G₂Q₂)∩(II₁) = I₂.

               G₂H₂I₂ – переріз трикутної призми.

 

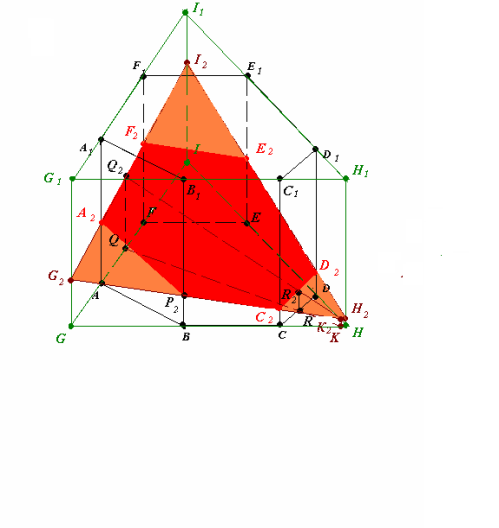
Рис.17.4

 

 

 

 

4.  (G₂I₂)∩(AA₁) = A₂ , (G₂I₂)∩(FF₁) = F₂,  (G₂H₂)∩(CC₁) = C₂ ,    (H₂I₂)∩(DD₁)= = D₂, (H₂I₂)∩(EE₁) = E₂ (рис.17.4).  

         A₂P₂C₂D₂E₂F₂ – шуканий переріз.

 

 

 

 

 

 

 

 

 

Задача 2.

Bикористовуючи метод доповнення  п – кутної піраміди  до трикутної , побудувати переріз піраміди SABCDE площиною (Q₂P₂R₂), якщо Q₂ є (AES), P₂ є [SB], R₂ є [SC](рис.18.1).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

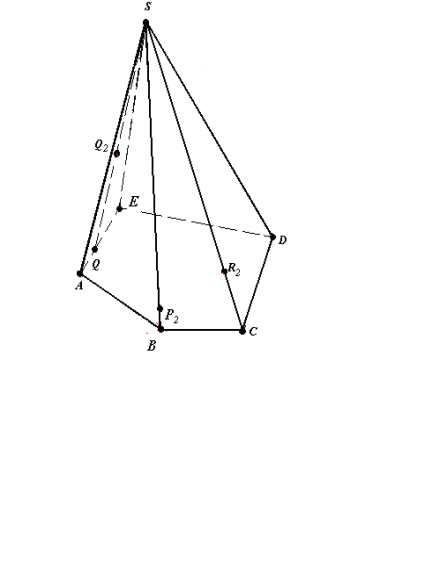
Рис.18.1

1. Q  - проекція Q₂ на площину основи,

                 B - проекція P₂ на площину основи,

         C  - проекція R₂ на площину основи.

         Зображення  (рис.18.1) повне.

 

 

 

 

 

 

 

 

 

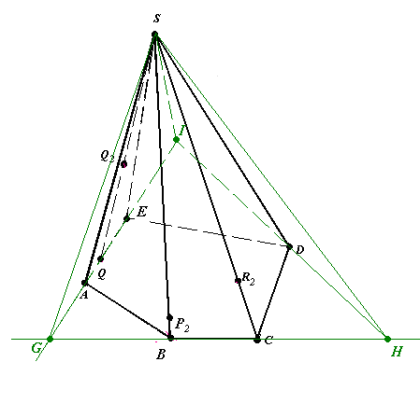
Рис.18.2

 

 

 

2. SGHI – доповнена трикутна піраміда, причому

P₂ є (GHS), R₂ є (GHS), Q₂ є (GIS) (рис.18.2).

 

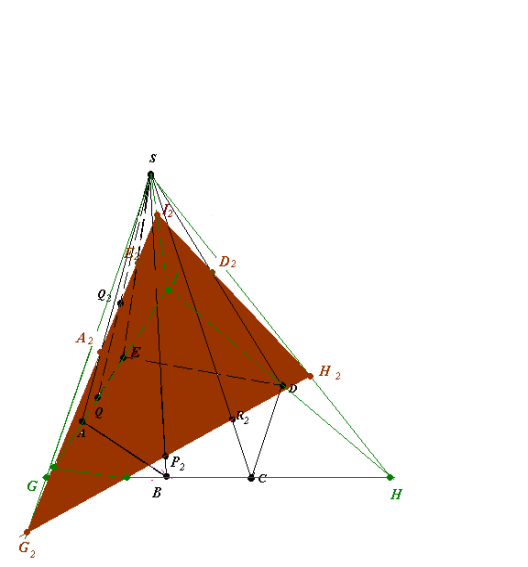
Рис.18.3

 

 

3. (P₂R₂)∩(SH) = H₂, (P₂R₂)∩(SG) = G₂, (G₂Q₂)∩(SI) = I₂,(рис.18.3)

G₂H₂I₂ – переріз трикутної піраміди SGHI.

 

 

 

 

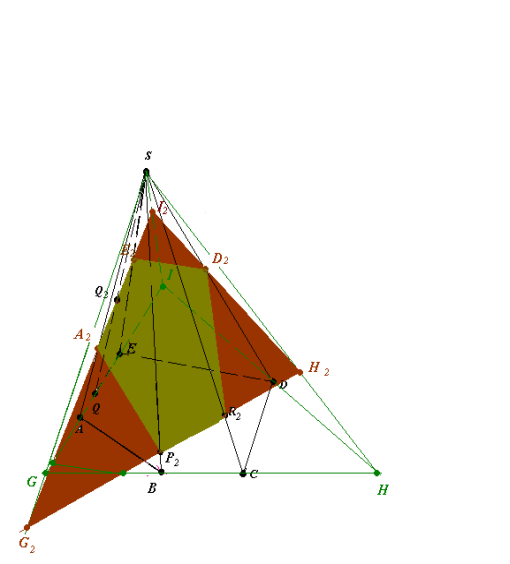
Рис.18.4

 

 

4. (G₂I₂)∩(AS) = A₂, (G₂I₂)∩(ES) = E_{2 ,}(I₂H₂)∩(DS) = D₂(рис.18.4)

       E₂A₂P₂R₂D₂ – шуканий переріз.

 

2.6. Метод паралельних прямих

 

Алгоритм побудови перерізу

1.  Перевіряємо повноту зображення.
2. Коли врахувати, що лінії перерізу паралельних площин площиною перерізу паралельні, то, маючи лінію перерізу на одній з паралельних площин і точку на іншій, будуємо пряму, інцидентну цій точці і паралельну лінії перерізу першої площини.
3. Визначаємо площину шуканого перерізу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задача 1.

Bикористовуючи метод паралельних прямих , побудувати переріз призми ABCDEFA₁B₁C₁D₁E₁F₁ площиною (Q₂P₂R₂), якщо Q₂ є (AA₁F₁F), P₂ є [BB₁], R₂ є (CC₁D₁D) (рис.19.1).

 

 

Рис.19.1

 

 

1.                Q  - проекція Q₂ на площину основи,

                 B - проекція P₂ на площину основи, 

                 R - проекція R₂ на площину основи. 

                 Зображення (рис.19.1) повне.

 

 

 

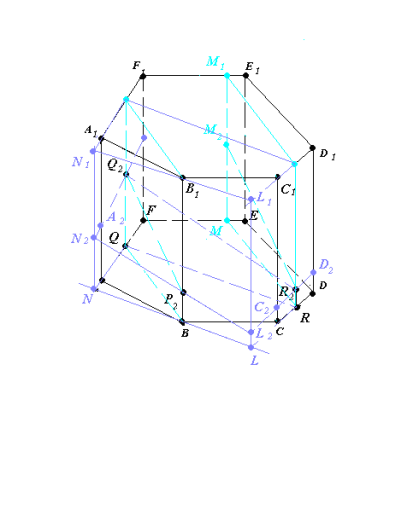
Рис.19.2

 

 

 

 

2. Побудуємо площину (R₂RM)║(P₂BQ)

             та проведемо (R₂M₂)║(P₂Q₂) (рис.19.2).

   Побудуємо площину (N₁NB)║(Q₂QR₂),  (N₁NB)∩(D₁DC)=(LL₁).

              та проведемо (P₂N₂)║(R₂Q₂), (P₂N₂)∩(LL₁)=L₂.

 

 

 

 

 

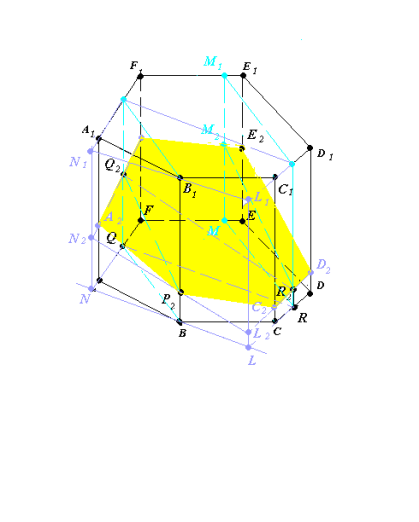
Рис.19.3

 

 

 

(N₂Q₂)∩(AA₁) = A₂ , (N₂Q₂)∩(FF₁) = F₂, (L₂R₂)∩(DD₁) = D₂ ,   (L₂R₂)∩(CC₁)=C₂, (F₂M₂)∩(EE₁) = E₂ (рис.19.3).

 

 

 3.  A₂P₂C₂D₂E₂F₂ – шуканий переріз.

 

 

 

 

 

 

Задача 2.

Bикористовуючи метод паралельних прямих , побудувати переріз піраміди SABCDE площиною (Q₂P₂R₂), якщо Q₂ є (AES), P₂ є [SB], R₂ є [SC] (рис.20.1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис.20.1

 

 

 

1. Q  - проекція Q₂ на площину основи,

         B - проекція P₂ на площину основи,

         C - проекція R₂ на площину основи.

         Зображення (рис.20.1) повне.

 

 

 

 

 

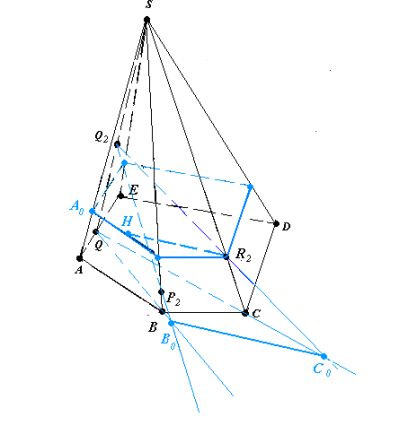
Рис.20.2

 

 

 

2.          Через точку R ₂ проведемо площину µ║(ABC)

          та проведемо (R₂H)║(B₀C₀), де B₀=(Q₂P₂)∩(QB),

          C₀=( Q₂R₂)∩(QC) (рис.20.2).

 

 

 

 

 

 

 

 

 

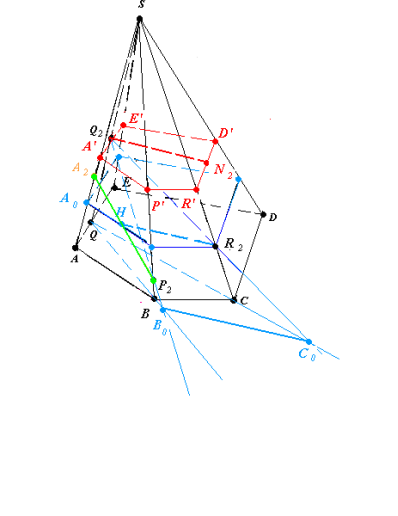
       Рис.20.3

 

 

 

Через точку Q ₂ проведемо площину ß║(ABC),                                                   ß∩(Q₂P₂R₂)=(Q₂N₂) (рис.20.3).

 

 

 

 

 

 

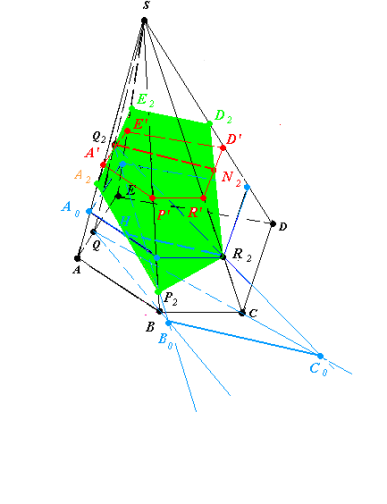
Рис.20.4

 

 

 

 

(R₂N₂)∩(SD) = D₂ , (P₂H)∩(SA) = A₂, (A₂Q₂)∩(SE) = E₂ (рис.20.4) .

 

      3.  A₂P₂R₂D₂E₂ – шуканий переріз.

 

 

 

3. ВИСНОВКИ ТА ПРОПОЗИЦІЇ

 

Мета посібника - показати різноманітність і красу геометричних побудов, привернути спочатку мимовільну увагу учасників проекту, продовжувати розвивати просторову уяву; показати простоту і доступність викладеного.

Кожен з п’яти методів побудови являє собою алгоритм, що складається з трьох – чотирьох пунктів. Наявність електронного варіанту посібника забезпечує можливість за лічені хвилини представити будь-який з методів у вигляді презентації і продемонструвати.

Який же з запропонованих методів вибрати вчителю при мінімальній кількості відведених для вивчення теми  годин? У переважній більшості сучасних посібників розглядаються метод слідів, метод внутрішнього проектування та комбінований метод, який поєднує в собі два згаданих. Погодьтеся, що, розв’язуючи задачу, значно простіше виконувати побудову прямої, провівши її через дві задані точки, ніж побудову  прямої паралельної до заданої. Тому способи побудови перерізів, розглянуті у параграфах 2.5 і 2.6 є дещо складнішими. А метод поділу n-кутної призми (піраміди) на трикутні майже не відрізняється по суті своїй від методу внутрішнього проектування.

 Даючи відповідь на запитання ,вибір якого з методів є оптимальним (метод слідів, чи метод внутряіішнього проектування), проведемо практичне дослідження. Змінивши розміщення заданих точок Q₂, P₂ і R_2, згідно умови задачі 1 п.2.2 ст.22 бачимо, що алгоритм побудови перерізу методом слідів у цьому випадку застосувати неможливо:

 

 

 

 

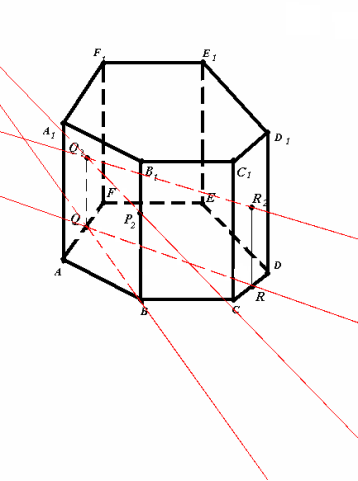
Тому пропоную при обмеженій кількості годин перевагу надавати вивченню методу внутрішнього проектування. І все таки право вибору залишається за вами, шановні колеги.

 

 

 

 

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

 

 

1. Атанасян Л.С. , Базылев В.Т. Геометрия. Учебное пособие для студентов физ.- мат. факультетов педагогических институтов В 2 ч. Ч. 2. – М.: Просвещение, 1987. с.119-125.
2. Болтянский В.Г. Элементарная геометрия. Кн. Для учителя. – М.: Просвещение, 1985.- 320 с.
3. Гольдберг Я.Е. С чего начинается решение стереометрической задачи: Пособие для учителя. – К.: Рад. шк., 1990.
4. Жовнір Я.М. Позиційні задачі в стереометрії: Посібник для вчителя. – К.: Освіта, 1991. – с.25 – 41, 57-93.
5. Конфорович Ф.Г. Математичні софізми і парадокси.- К.: Рад. школа, 1983.
6. Литвиненко В.Н.  Задачи на развитие пространственных представлений: Кн. Для учителя.- М.: Просвещение, 1991.
7. Погорєлов О.В. Геометрія: Стереометрія: Підручник длля 10-11 класів середньої школи.- 2-ге вид. – К.: Освіта, 1995. – 128 с.
8. Програми для загальноосвітніх навчальних закладів. Навчальні програми для профільного навчання. Програми факультативів, спецкурсів, гуртків. Математика. –К.: «Навчальна книга», 2003. – 302 с.
9. Савченко В.М. Изображение фигур в математике. – К.: «Вища школа», 1978.
10. Тесленко І.Ф., Боровик В.М. Практикум з розв’язування задач. Геометрія. – К.: «Вища школа», 1978.
11. Токар Н.Г., Вельдбрехт Д.О. Правильні многогранники // Математика. – 2002.- № 22-23 (177-178). – с.126-128.
12. Черкасов Р.С., Столяр А.А. Методика викладання математики в середній школі. – Х.: «Основа», 1992.