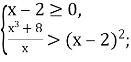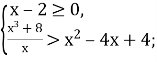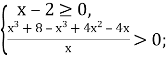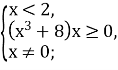Ірраціональні нерівності. Їх види.

Найпростіші ірраціональні нерівності

 

Означення ірраціональної нерівності в різних підручниках дається по - різному. Наприклад, в підручнику для 11 класу вказано, що «ірраціональні нерівності містять змінну під знаком кореня або під знаком степеневої функції з дробовим показником» . Але на мою думку, більш вдалим є таке означення «ірраціональними називають нерівності виду f(х) g(х), або f(х) g(х), де f(х) і g(х) – деякі алгебраїчні функції, причому принаймні одна із них є ірраціональною відносно змінної х» . Прикладами ірраціональних нерівностей є: + та інші.

Часто ірраціональні нерівності розв’язують за аналогією до ірраціональних рівнянь. При розв’язані нерівностей, які містять корені непарного степеня, це нічим суттєво не відрізняється, адже при піднесенні обох частин нерівності до непарного степеня, дістанемо нерівність рівносильну даній. Це підтверджують такі дві теореми:

Теорема 1. Нерівність виду рівносильна нерівності

f(х) g(х))²ⁿ⁺¹.

Теорема 2. Нерівність виду рівносильна нерівності

f(х) <g(х))²ⁿ⁺¹, де f(х) і g(х) – раціональні функції  від х, n – деяке натуральне число.

При піднесенні обох частин ірраціональної нерівності до парного степеня, отримаємо рівносильну нерівність тільки в тому разі, якщо при всіх х з області допустимих значень, обидві частини нерівності невід’ємні.

Основним методом розв’язування ірраціональних нерівностей є метод зведення вихідної нерівності до рівносильної системи раціональних нерівностей або сукупності таких систем.

У збірнику для ДПА з математики для 11 класу є багато завдань на розв’язання ірраціональних нерівностей, представлених у вигляді добутку двох множників (один з яких ірраціональний вираз), який більший або менший нуля. Наприклад, (2х-1) , ,   та інші.

Трудність викликають ті нерівності, в яких один із множників є тригонометричним або логарифмічним  виразом.

Для прикладу розв’яжемо нерівність () із 20 варіанту (ІV рівень).

Складемо систему:                

Розв’яжемо першу нерівність:     х(х – 3) = 0,      

 

    +                 -                   +   
                      0                3                   х                 х[ 0; 3].

Розв’яжемо другу нерівність: ,

,  ,    

,  ,  , n.

Знайдемо розв’язок системи:

0                 3       х

 

.

 

Відповідь: .

 

Нерівності виду і

 

          Найчастіше зустрічаються нерівності і . Розв’язування ірраціональних нерівностей такого виду зводиться до розв’язування сукупності двох систем раціональних нерівностей. Це дозволяє зробити така теорема:

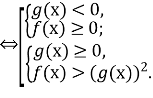    і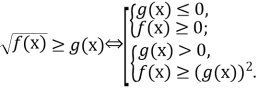    

Для прикладу  розв’яжемо нерівність із 15 варіанту ДПА   . 

Складемо системи нерівностей:

2.        

          

0            2                    х

 

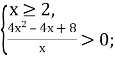
Оскільки D = 1 – 8 = -7 і , то  .  Отже, .

3.           

Оскільки D = 2 – 16 = -14 тому дана система рівносильна системі

 

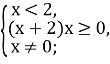
Нерівність ,   ,  х₁ = -2;  х₂ = 0.

 

    +                 -                   +   
                      -2               0                  х        

Розв’язком системи буде:

0        2         х

     

 

 

Відповідь:

Нерівності виду і

 

Розв’язати нерівність можна, користуючись теоремою.

Теорема. Нерівність , де f(х) і g(х) – раціональні функції від х, а n- деяке натуральне число, рівносильна системі нерівностей: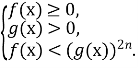

Значить буде рівносильна такій системі:

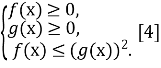[4]

Розв’яжемо нерівність

Користуючись теоремою, маємо:

               

          

                 

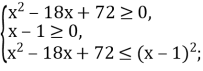
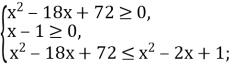
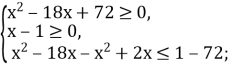
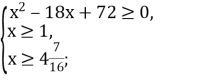
Розв’яжемо першу нерівність системи: за теоремою Вієта х₁=6, х₂=12.  

 

     +               -                   +   
             6                12                    х            х (-.

Розв’язком системи є:

6                  12          х

х

 

 

Відповідь: х

Нерівності виду і

 

Нерівності і можна звести до системи таким чином:      

          Розв’язуючи нерівність ,

дістанемо систему: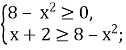

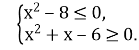
Перша нерівність       (х-2) (х+2)  має розв’язки 

  

       +                   -                   +   
                               2                 х        х

Тоді система нерівностей має розв’язки:

-2             2        2      х

 

х

 

Відповідь: х.

 

Нерівності виду ,

 

Користуючись означенням арифметичного кореня, можна записати нерівності , таким чином: 

Розглянемо  нерівність  2.

Саме ця нерівність  була у 33 завданні ЗНО 2009р. Розв’яжемо її:

,  ,

–   Знайдемо нулі 1підмодульних виразів: , звідки х=3,  х= -1.   Вони розбивають числову пряму на три проміжки.

Розкриємо знак модуля на кожному з них:

Якщо х, то  -2(х – 3) + (х + 1) х,  -2х + 6 + х + 1х, -2х -7, х3,5.

-1                       3,5                  х

 

 

х.

Якщо х [-1; 3], то  -2(х – 3) – (х – 1) х,

-2х + 6 –х + 1 х, -4х -7, х

х

 

   х.

 

Якщо ж х (3; ), то 2(х – 3) – (х – 1) х, 2х – 6 – х + 1 0х . Нерівність правильна для всіх х (3; ).

Відповідь: х [1,25; ].

 

Нерівності виду

 

        Нерівності можна розв’язати за таким алгоритмом:

1. Ввести нову змінну.
2. Знайти значення цієї змінної, розв’язавши нерівність, що утворилась.
3. Повернутись до початкового невідомого.
4. Розв’язати утворені нерівності.

Розв’яжемо нерівність

     

                

       

Нехай = y, тоді отримаємо нерівність y ,

    за теоремою Вієта у₁=5;   у₂= -4.

     +               -                   +     

                           5                    х           

Повернемося до початкового невідомого.

     

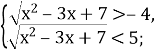
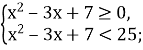
Розв’яжемо кожну нерівність.

1)   х²-3х+7=0, D = -19 0. Отже, нерівність правильна при всіх х.

2) , ,  D = 9 + 72 =81,

=9;  х₁ =6,    х₂= -3.

         +               -                   +   
                             6                  х     х.

Відповідь: х.

 Нерівності виду ,

та .

 

Щоб розв’язати такі нерівності, спочатку потрібно знайти область визначення вихідної нерівності.

Для цього розв’яжемо систему: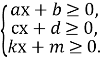        

Потім потрібно переписати нерівність в такому вигляді, щоб обидві її частини набували тільки додатних значень, а тоді піднести обидві частини до квадрата. Внаслідок цього дістанемо нерівність, рівносильну даній.

Дано нерівність .

Перепишемо її у вигляді: .

Знайдемо область визначення нерівності:

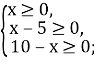
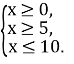                                     х.

Піднесемо обидві частини нерівності до квадрата:

х + 2 + х – 5 10 – х,          2

Тоді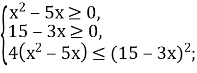                

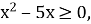
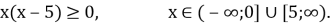
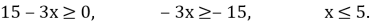
1.      
2. 
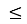
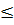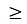
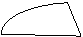3. 4(х² -5х) (15 – 3х)²,  4х² -20х 225 – 90х + 9х², 5х² – 70х + 225 0,    
4.   х² – 14х + 45 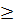0,            х² – 14х + 45 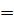0,  За теоремою Вієта х₁= -9, х₂= 5.

     +                 -                   +   
                           5                    х         х.

Але враховуючи область визначення, розв’язком вихідної нерівності є

Відповідь: .