Із досвіду роботи вчителя математики Олещук Любов Анатоліївни за Програмою курсу за вибором «Логічними стежинками математики»

Відділ освіти Снігурівської районної державної адміністрації

Снігурівський районний методичний кабінет

Снігурівська загальноосвітня школа І – ІІ ступенів №3

 

Із досвіду роботи вчителя математики

Олещук Любов Анатоліївни

за Програмою курсу за вибором

«Логічними стежинками математики»

 

 

 

 

 

 

 

 

2019 р.

 

Упорядник: Л. А. Олещук, вчитель математики Снігурівської ЗОШ І –ІІІ ступенів №3, Снігурівської районної ради Миколаївської області, спеціаліст вищої категорії.

Рецензенти: З. Я. Карташова, керівник районного методичного об’єднання вчителів математики, спеціаліст вищої категорії, вчитель- методист.

Л. М. Резнік, вчитель трудового навчання Снігурівської загальноосвітньої школи І – ІІІ ступенів №3, Снігурівської районної ради Миколаївської області, спеціаліст вищої категорії, вчитель- методист, відмінник освіти України, керівник районного методичного об’єднання вчителів трудового навчання.

Консультант: О. В. Шиян, методист районного кабінету відділу освіти Снігурівської районної державної адміністрації.

Відповідальна за випуск: Л. В. Горностай, завідувач районного методичного кабінету Снігурівської районної державної адміністрації.

Робота представлена на засіданні районного методичного обєднання вчителів математики, січень 2019 р.

На фото: фрагмент навчального заняття з учнями 5 класу.

Посібник адресований учителям математики для організації роботи з розвитку творчої особистості учня.

 

 

 

Зміст

1. Вступ
2. Методичні рекомендації щодо реалізації програми за вибором
3. Зразки занять з математичної логіки
4. Логічні задачі рекомендовані для використання на уроках математики
   1. Пошукові задачі
   2. Задачі на кмітливість
   3. Уроки логічної грамотності

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

Сучасне суспільство змінюється досить швидко, тому важко прогнозувати навіть найближче майбутнє. Неможливо передбачити, які конкретні знання можуть знадобитися випускникові в його житті, а які – ні. Для сьогоднішнього випускника навчального закладу важливо володіти вмінням мислити, добувати і переробляти інформацію, аналізувати ситуацію, адекватно оцінювати результати, бути завжди зрозумілим у викладі своїх думок людям, які його оточують, уміти конструктивно взаємодіяти з іншими.

Вчитель повинен працювати над розв’язанням таких завдань, як: розвиток в учнів поняттєвого мислення, якостей мислення, а саме – гнучкості, дивергентності, глибини, критичності й самостійності; вміння аналізувати ситуацію, планувати свої дії на кілька кроків вперед, адекватно оцінювати результати, самостійно добувати і переробляти інформацію, конструктивно взаємодіяти з іншими людьми.

Мета занять курсу за вибором «Логічними стежинками математики»:

• інтелектуальний розвиток учнів, формування в них послідовного пошукового логічного мислення, просторової уяви, здатності до самостійного опрацювання інформації, моделювання розв’язання нестандартних задач;
• створення умов для розвитку природних математичних здібностей та обдарувань кожної особистості з урахуванням її вікових особливостей;
• розвиток таких рис особистості, як винахідливість, кмітливість, зосередженість;
• підвищення рівня математичної культури школярів;
• задовольнити потреби профільної математичної підготовки учнів.

На кожне заняття ставлю задачі:

• розвивати в учнів зацікавленість до предмету;
• ознайомити учнів з деякими зональними математичними ідеями;
• навчити учнів формулювати окремі логічні кроки у пошуку моделі розв’язання, представляти модель розв’язку через послідовні логічні кроки;
• розвивати в учнів нестандартне логічне мислення, пошукову активність;
• ознайомити учнів з різними методами розв’язування задач логічного характеру.

Розв’язування будь-якої задачі тією чи іншою мірою базується на проведені певних роздумів. Більшість задач цього курсу – це задачі, які можна розв’язати майже без обчислень. Для цього потрібні тільки послідовні логічні міркування, бажання, наполегливість, кмітливість і терпіння. Розв’язання таких задач учить аналізувати, порівнювати, робити висновки, а іноді і шукати нестандартні способи розв’язування.  Такі вміння допоможуть учням у майбутньому не тільки оволодіти математичною чи іншою найкою, а ще й в житті не ховатися від проблем, якщо розглядати їх, як життєві задачі та шукати шляхи вирішення.

«Математика – це велетенський пінцет наукової логіки»

Дж. Голстед

«Якщо ви власними силами розв’язали задачу, ви зробили відкриття. Якщо задача нескладна, то ваше відкриття не може претендувати на грандіозність; проте воно від цього не перестає бути відкриттям»

Д. Пойя

Методичні рекомендації щодо реалізації програми за вибором

1. Важливо підбирати «посильні задачі підвищеної складності», щоб не відштовхнути учнів, не зменшити зацікавленості їх відповідною тематикою.
2. Бажано не забувати психологічного аспекту: починати з очевидного, життєвого з поступовим ускладненням та абстрагуванням.
3. Дати можливість учням відчути саме смак напруження і пошуку, пережити відчуття перемоги над задачею, повірити себе.
4. Нагадуйте учням структуру логічного кроку міркування, пропонуйте в пошуку розв’язку та в запису розв’язування виділяти та нумерувати логічні кроки міркувань
5. Пропоную повертатися до теми «Просторова уява і площина паперу» декілька разів протягом навчального курсу з метою поступового удосконалення в учнів просторової уяви.
6. Зверніть увагу на раціональність усного рахунку учнів, уміння здійснювати оцінку числа. Навички такого рахунку впливає на загальну математичну підготовку учнів.
7. Звертайте увагу на можливість схематичного оформлення моделі розв’язання. Це сприяє формуванню в учнів здатності до моделювання, розгалуженого мислення.
8. Не забувайте фіксувати зв’язки між способами розв’язування начебто різних задач, здійснювати узагальнення, підкреслювати відмінність ідей розв’язань. Усе це сприятиме формуванню в учнів математичної культури мислення.
9. Використовуйте кольорову крейду, а учням пропонуйте використовувати кольорові олівці. Колір допомагає виділити головне, відокремити об’єкти, залучити зорову увагу та пам'ять учнів.

«Математика цікава тоді, коли живить нашу винахідливість і здатність міркувати» Д. Пойя

Зразки занять з математичної логіки

Заняття №1. Тема: Задачі – жарти.

Мета:

• Формування предметних компетентностей: ознайомити та зацікавити учнів нескладними задачами логіки; навчити пояснювати логічні операції та розв’язувати завдання на інтуїтивній основі; розвивати мовлення учнів та логічне мислення; виховувати старанність та наполегливість.
• Формування ключових компетентностей:

уміння вчитися: формувати здатність виконувати завдання в певній послідовності;

загальнокультурної: формувати навички дотримування норм культурної поведінки;

здоров’язбережувальної: сприяти дотриманню норм гігієни читання і письма.

Обладнання: таблиця з фігурами, сигнальні картки.

Хід заняття

І. Вступна частина

1. Організація класу

Завдання «Чи вмієш орієнтуватися в просторі?»

По вузькій стежинці йшли один за одним ведмідь, вовк, заєць. Хто йшов за ким? Перед ким? Хто йшов між ким? Хто йшов першим? Останнім? Середнім?

Математична мозаїка

Розгляньте уважно числову таблицю. Запишіть числа, які пропущені. Визначте закономірність запису чисел в кожному рядку.

1, 3, 5, 7, 9, 11, 13, …

2, 4, …, 8, 10, 12, …, 16

3, 6, 9, …, 15, …, 21, 24

Після спілкування в парах учні роблять висновки:

1. В першому рядку записані непарні числа.
2. В другому рядку всі числа парні, які діляться на 2.
3. В третьому рядку всі числа, які діляться на 3.

2. Оголошення теми і мети заняття

Сьогодні ми будемо розв’язувати логічні вправи, задачі – жарти. Це задачі, які можна розв’язати без обчислень. Для цього потрібні тільки послідовні логічні міркування.

«Хто швидше?»

На столі лежать три олівці. Як переставити середній олівець, не чіпаючи його? Подумайте і зробіть це.

ІІ. Основна частина

1. Актуалізація опорних знань

Індивідуальна, самостійна робота

Розмістити в порожніх клітках числа так, щоб сума трьох чисел, розміщених по прямих становила 18.

 

 

 

Робота в групах

Поспілкуйтесь і поставте знаки дій між числами так, щоб виконувалася рівність: 0 1 2 3 4 5 6 7 8 9 = 100

Колективно – групова робота

Приклад 1. У Вінні Пуха та П’ятачка в кишенях однакова кількість монет. Скільки монет П’ятачок повинен дати Вінні-Пуху, щоб у ведмедика стало на 4 монети більше?

Приклад 2. Пляшка соку коштує 10 грн. Сік на 9 гривень дорожчий за пляшка?

Розв’язання:

Нехай пляшка коштує р грн., а сік – с грн..

1. р + с = 10 грн.
2. с = 9 + р.
3. р + (р + 9) = 10, пляшка коштує 0,5 грн, а сік – 9,5 грн.

Відповідь: порожня пляшка коштує 0,5 грн.

Приклад 3. Є дві монети, сума яких 15 коп., але одна з них - не п’ятак. Що це за монети?

Розв’язання

Одна з двох монет - не п’ятак. Тоді друга з них може бути п’ятаком.

Відповідь: 10 коп. і 5 коп.

Приклад 4. Є 5 гномів. Їм показали 3 червоних та 4 синіх капюшони. У темряві на них одягли 3 червоних та 2 синіх капюшони, а інші сховали. Хто із цих гномів може визначити колір свого капюшона після того, як ввімкнуть світло?

Розв’язання

Проаналізуємо, що побачать гноми, коли ввімкнуть світло.

1.     Гном у червоному капюшоні побачить, що на інших одягли 2 синіх і 2 червоних капюшони. Тоді його капюшон може бути, як червоний, так і синій (оскільки всього було 3 червоних і 4 синіх капюшони).
2.     Гном у синьому капюшоні побачить, що на одному синій і на трьох червоні капюшони. Тоді його капюшон може бути тільки синім.

Відповідь: гноми в синіх капюшонах.

Завдання для самостійної роботи

1.     Мати Петрика має трьох синів. Першого вона назвала Іваном, а другого – Грицьком. Як звуть її третього сина? (Відповідь: Петриком).
2.     П’ять рибалок з’їли п’ять судаків за п’ять днів. За скільки днів десять рибалок з’їдять десять судаків? (Відповідь: 5 днів).
3. Сьогодні о 12 годині ночі пішов дощ. Чи може бути сонячна погода через 72 години? (Відповідь: ні, бо буде ніч).
4.     Скільки кінців у двох палок? А в чотирьох із половиною? (Відповідь: 4; 10).
5.     Стрічку розрізали на 10 частин. Скільки розрізів було зроблено? (Відповідь: 9).
6.     Круглий кекс із діркою посередині розрізають на 10 частин (на сектори). Скільки розрізів зроблено? Чому відповідь інша, ніж у задачі №5? (Відповідь: 10).
7.     Відстань між стовпами огорожі повинна дорівнювати 2 м. Скільки стовпів потрібно, щоб огородити прямокутну ділянку зі сторонами 10 і 20 м? (Відповідь: 30).

ІІІ. Заключна частина

1.     Рефлексія

Вправа «Мікрофон»

Загадки – жарти

1.     В якому місяці діти найменше плачуть? (У лютому)
2.     Коли година має менше ніж 60 хвилин? (Коли вона академічна – урок триває 45 хв)
3.     Назвіть підряд п’ять днів тижня, не використовуючи назв днів і порядкових чисел. (позавчора, вчора, сьогодні, завтра, післязавтра)
4.     За який час на сковорідці можна піджарити 3 шматка хліба, якщо на підсмажування одного шматка потрібно 1 хв? (1 хвилина)
5. Один учень розв’язав задачу за 1 год. За який час розв’яжуть цю задачу 10 учнів? (1 годину)
6. Маринка відпочивала в санаторії 3 тижні і 2 дні. Скільки всього днів відпочивала Маринка? (23 дні)
7. 10 насосів за 10 хв викачують 10 т води. За скільки хвилин 25 насосів викачають 25 т води? (10 хв)

2. Домашнє завдання

Скласти задачу – жарт.

 

Заняття №2. Тема: Задачі – загадки.

Мета:

• Формування предметних компетентностей: формувати в учнів уміння розгадувати та складати математичні загадки; розвивати спостережливість, зацікавленість, критичне мислення, просторову уяву учнів; виховувати працьовитість, старанність, любов до математики.
• Формування ключових компетентностей:

уміння вчитися: формувати здатність переключатися з одного виду роботи до інших;

загальнокультурної: сприяти дотриманню норм культурної поведінки.

Обладнання: таблиця, сигнальні картки.

Хід заняття

І. Вступна частина

1. Організація класу

Гра «Хто швидше?»

• Скільки кінців у трьох палок?
• Є 18 м тканини. На пошив костюмів щодня відрізали по 3 м. На який день відрізали останній раз?
• У кошику лежало 5 яблук. Чи можна поділити їх порівну між 5 товаришами так, щоб одне яблуко залишилось у кошику?

2. Оголошення теми і мети заняття

У математиці зустрічається багато задач без числових даних. Але ці задачі легко розв’язуються шляхом порівняння, співставлення, узагальнення.

Задача. У трьох коробках лежить по олівцю: жовтий, червоний, зелений. На першій коробці написано «жовтий», на другій – «червоний», на третій – «жовтий або зелений». Олівець якого кольору лежить у кожній коробці, якщо жодний із записів не відповідає дійсності?

Відповідь: у І коробці – зелений, у ІІ коробці – жовтий, у ІІІ коробці – червоний.

ІІ. Основна частина

Розв’язування задач

1. Гном пчихає щопівгодини. Упродовж якого проміжку часу гном пчихне тричі? (Відповідь: протягом 1 години)
2. Як розрізати кавун на чотири частини так, щоб після того, як їх з’їдять, залишилось рівно п’ять шкоринок? (Ламати або розрізати додатково шкоринки не можна). Відповідь: спочатку відрізати циліндр із середини кавуна, що обмежений двома шкоринками (зверху та знизу). Потім залишок розрізати на 3 частини.
3. Під однією парасолькою сховалися: шестеро дітей, троє дорослих, дві кішки, собака та два кролики. У якому випадку ніхто не намокне? (Відповідь: якщо не буде дощу).
4. Колесо має 12 спиць. Скільки проміжків між спицями? (Рахуємо лише проміжки між сусідніми спицями.) Відповідь: 12.
5. Кекс коштує 1 грн і ще половину такого самого кексу. Скільки коштує один кекс? (Відповідь: 2 грн).

А тепер уперед – у самостійні дедуктивні розслідування! Не намагайтесь вгадати відповідь, а міркуйте, формулюйте логічні кроки!

Завдання для самостійної роботи

1. Скільки всього існує двоцифрових чисел? А трицифрових? (Відповідь: 90; 900.)
2. Нехай у Вас і в мене однакові суми грошей. Скільки гривень я маю Вам віддати, що у Вас стало на 10 грн більше, ніж у мене? (Відповідь: 5 грн.)
3. Пляшка молока коштує 10 грн. Відомо, що молоко на 9 грн дорожче за пляшку. Скільки коштує порожня пляшка? (Відповідь: 50 коп.)
4. Бідон з морозивом важить 34 кг, а бідон, наполовину наповнений морозивом, – 17 кг 500 г. (Відповідь: 1 кг.)
5. Одна конячка пробігає шлях від села до міста за 4 години. За скільки хвилин доскачуть із цього села до міста дві конячки? А чотири? (Відповідь: 240 хв.)
6. Скільки разів за добу годинна стрілка минає цифру 1? А хвилинна за 5 годин? А секундна за 5 хвилин? (Відповідь: 10; 25; 25.)

Робота в групах

1.     Кінь і віслюк везли мішки. Кінь каже: «Мені важче, ніж тобі. Коли б я узяв у тебе мішок, у мене стало б удвічі більше, ніж у тебе, а коли ти візьмеш у мене мішок, їх у нас стане порівну». Скільки мішків віз кінь і скільки віслюк? Відповідь: 7; 5.
2.                                                                                                                                                                                                       Двома лініями поділіть чотирикутник на 4 частини так, щоб серед них були:

А) усі трикутники;

Б) 2 трикутники, 2 чотирикутники;

В)3 трикутники і 1 чотирикутник.

ІІІ. Заключна частина

1. Рефлексія

Гра «Так чи ні?»

Сигнальні картки: зелена – так, червона – ні.

1. Якщо я віддам 4 марки Оленці, то в неї буде на 8 марок більше, ніж у мене. Так чи ні? (Так.)
2. Якщо одна шоколадка коштує 10 грн та половину шоколадки. Отже шоколадка коштує 10 грн. Так чи ні? (Ні.)
3. Яйце вариться 5 хвилин, тоді воно вважається звареним. Отже 5 яєць можна зварити за 25 хвилин. Так чи ні? (Ні.)
4. Поле поділено на дві ділянки. На кожній ділянці пасуться три корови і дві вівці. Скільки всього тварин пасуться на полі? Я говорю, що дві. Так чи ні? (Так.)

2. Домашнє завдання

Підготувати по 2 загадки

 

Заняття №3. Тема: Розв’язування задач на кмітливість.

Мета:

• Формування предметних компетентностей: формувати в учнів уміння розв’язувати задачі; учити аналізувати, порівнювати, робити висновки; розвивати дитячі здібності і вміння, дати відчути смак навчальної праці; виховувати уважність, бажання пізнати нове та любов до математики.
• Формування ключових компетентностей:

соціальної: навчати продуктивно співпрацювати з учнями класу;

загальнокультурної: сприяти дотриманню норм культурної поведінки.

Обладнання: картки із завданнями, сигнальні картки.

Хід заняття

І. Вступна частина

1. Організація класу

Гра «Весела лічба»

1. Відгадайте ребуси

3 < ник;   7’я;   40а;   100лиця;  Г1а.

2. Відгадайте слова, в яких знаходиться цифра 3. (Вітрина, вітрила, актриса.)

2. Оголошення теми і мети заняття

Сьогодні ми будемо розвязувати задачі на кмітливість.

Порівняйте вирази за секунду, не виконуючи обчислен.

1. 7 + 7 + 7 … 7 * 4;
2. 9 * 6 – 9 … 9 * 5;
3. 17 + 17 + 17 … 17 * 4 – 17;
4. 6 * 8 … 6 + 6 + 6 + 6.

ІІ. Основна частина

Розвязування задач

Задача 1. Бабуся утримує собак і котів (разом їх 10). Якось вона приготувала 56 котлет і залишила їх холонути на столі. Через 5 хвилин котлет не стало – кожен кіт зїв по 5 котлет, а кожен собака – по 6. Скільки собак і скільки котів живе в бабусі?

Розв’язання

1. Якщо кожна з 10 тварин отримає по 5 котлет, то використано буде 50 котлет.
2. Маємо 6 «зайвих» котлет, які з’їли собаки.
3. 10 – 6 = 4 (коти).

Відповідь: 6 собак і 4 коти

Задача 2. Скільки у лісі звірів і скільки птахів, якщо в них разом 6000 ніг та 2500 голів?

Розв’язання

1. «Роздамо» кожній голові по одній парі ніг – маємо 5000.
2. Залишок 1000 ніг визначає кількість чотириногих – 1000 : 2 = 500.
3. Кількість двоногих (птахів) дорівнює 2500 – 500 = 2000.

Відповідь: 500 звірів і 2000 птахів.

Робота в групах

1. Три курки за три дні несуть 3 яйця. Скільки яєць знесуть ці курки за девять днів? (9)
2. На лавочці сиділо двоє: один нижчий, другий – вищий. Нижчий – син вищого, хоча вищий не його батько. Як ви це поясните? (на лавочці сидів син і його мати).
3. Ви сидите на вертольоті, перед вами верблюд, позаду – поні. Де ви? (на каруселі).
4. Два землекопи викопують 2 м канави за 2 год. Скільки потрібно землекопів, щоб за 4 год викопати 4 м канави? (2).
5. За дві груші дають три яблука, а за шість яблук – 15 слив. Скільки слив дадуть за 12 груш? (45 слив).
6. Уздовж вулиці побудовано 100 будинків. Майстра попросили виготовити номери на ці будинки. Скільки цифр 9 він має виготовити? (20).
7. Дах будинку асиметричний: один його бік нахилений під кутом 60⁰ до поверхні землі, а другий під кутом 70⁰. Півень відкладає яйця на гребені цього даху. У який бік впаде яйце? (Нікуди. Півні не несуть яйця).
8. Потяг відправляється з Києва до Львова. Через годину зі Львова відправляється інший потяг до Києва. Обидва потяги їдуть з однією і тією самою швидкістю. Машиніст якого з них у момент зустрічі потягів буде на меншій відстані від Києва? (Обидва потяги знаходяться на однаковій відстані від Києва).
9. Петрик живе на шостому поверсі, а Катруся – на другому. У скільки разів Петрику треба пройти більше сходинок, ніж Катрусі? (у 5 разів. Катруся проходить один сходовий марш, а Петрик -5).

Підведення підсумків.

ІІІ. Заключна частина

1.     Рефлексія

Обчисли швидко, але не помились!

•                    Скільки буде одиниць, якщо одну одиницю помножити на один десяток? (10 одиниць).
•                    Скільки буде десятків, якщо один десяток помножити на 1 десяток? (10 десятків).
•                    Скільки буде сотень, якщо одну сотню помножити на одну сотню? (100 сотень).
•                    Що треба зробити із числом 666, щоб збільшити його в півтори рази? (перевернути догори 999).
•                    У скільки разів сходи на 7 поверх довші від сходів на 2 поверх того самого будинку? (У 7 разів).
•                    Два півня можуть своїм співом розбудити одну людину. Скільки людей розбудять своїм співом 6 півнів? (Одну людину).
•                    Скільки граней має цілий шестигранний олівець? (8).
•                    Дві матері, дві доньки та бабця з онукою. Скільки всього родичів? (3).
•                    Мотоцикліст їхав з міста в село. На зустріч йому їхало дві машини. Скільки машин їхало в село? (Нуль).

2. Домашнє завдання

Підготувати ребус

 

Логічні задачі рекомендовані для використання на уроках математики

Пошукові задачі

І. Натуральні числа

1.     Приміський поїзд складається з шести вагонів. Василь і остап домовилися їхати в третьому вагоні. Як сталося, що вони їхали у різних вагонах? (Хлопці лічили вагони з різних кінців поїзда).
2.     З одного боку вулиці знаходиться парк, а з другого будинки. Скільки будинків на цій вулиці, коли кінотеатр є п’ятнадцятим, якщо будинки лічити як від початку, так і з кінця вулиці? (29 будинків).
3.     Котре з наведених чисел більше від суми трьох інших?

13005;   103001;   13007;   10301.

4.     Напиши найбільше десятицифрове число, всі цифри якого різні. (9876543210).
5.     Напиши найменше десятицифрове число, у якому всі цифри різні. (1023456789).
6.     На складі є ящики із цвяхами по 16 кг, 17 кг і 40 кг. Чи може комірник відпустити 100 кг цвяхів, не розкриваючи ящиків? (2∙(17+17+16)).
7.     Знайди найменше натуральне число, яке закінчується цифрою 6 і збільшується в 4 рази, якщо його останню цифру поставити на перше місце. (153846).
8. Написано підряд усі натуральні числа від 1 до 35. Скільки разів записана цифра «? Скільки разів ужито цифру 0? (Цифра 2 – 14 разів, цифра 0 – 3 рази).
9.     У книжці 104 сторінки. Скільки разів використали цифру 5 для нумерації сторінок цієї книжки? (20 разів).
10. Усі числа, які є номерами сторінок книжки, містять 371 цифру. Скільки сторінок у цій книжці, якщо на першій з них номер не друкується? (160 сторінок).

ІІ. Властивості додавання і віднімання

1.     Учень запам’ятав, що 9 + 7 + 8 = 24. Як можна скористатися цим результатом при додаванні чисел:

1.     29 + 27 + 28 + 39 + 37 + 38;
2.     309 + 307 + 308 + 209 + 207 + 208?

2.                  Обчисли найбільш раціональним способом:

1.     253 + 219 + 4200 + 781 + 647;
2.     5327 + 3889 – 197 – 499.

3.                  Чи може сума трьох чисел дорівнювати сумі двох із них? (Може, коли один із доданків нуль).
4.                  На уроці вчитель математики запропонував знайти суму перших двадцяти натуральних чисел. Тарасик звернув увагу на те, що 1 + 20 = 2 + 19 = 3 + 18 = … Як скористатися цим для знаходження суми? (10 ∙ 21 = 210).
5. Якою цифрою закінчується значення виразу:

1. 26 ∙ 27 ∙ 28 ∙ 29 + 51 ∙ 52 ∙ 53 ∙ 54; (8)
2. 41 ∙ 42 ∙ 45 ∙ 47 – 37 ∙ 39 ∙ 41 ∙ 43? (1)

ІІІ. Множення і ділення

1.     Віднови цифри, замінені у записах дій зірочками:

 

			2	3	*
		х	5	*	4
			*	*	*
*	*	*	0
*	*	*	*	*	4

		*	*	5
	х	1	*	*
	2	*	*	5
1	3	*	0
*	*	*
4	*	7	7	*

			*	1	*
		х	3	*	2
			*	3	*
	3	*	2	*
*	2	*	5
1	*	8	*	3	0

 

 

 

 

 

Відповідь: 236 ∙ 504; 325 ∙ 147; 415 ∙ 382.

2.     Знайди помилку:

1.                 (232 323 + 323 232) : 555 = 1001;
2.                 (414 141 + 141 414) : 55 = 111;
3.                 (313 131 + 242 424) : 5 = 111 111;
4.                 (424 242 + 242 424) : 66 = 10 101.

3.     Обчисли: 77 777 777 : 77 + 77 777 777 : 7777 + 77 777 777 : 7. (12131213)
4.     Скільки нулів буде в кінці добутку усіх натуральних чисел:

1.                 від 1 до 20 (чотири нулі);
2. від 15 до 35? (шість нулів).

5.           Перемножуючи числа 17 і 32, Олеся записала такі рівності: 17 ∙ 32 = 34 ∙ 16 = 68 ∙ 8 = 136 ∙ 4 = 272 ∙ 2 = 544. Далі вона множила числа 29 і 33: 29 ∙ 33 = 29 + 29 ∙ 32; 29 ∙ 32 = 58 ∙ 16 = 116 ∙ 8 = 232 ∙ 4 = 464 ∙ 2 = 928. Тоді 928 + 29 = 957. Якими властивостями дії множення скористалася Олеся? Обчисли таким способом 23 ∙ 64.
6. Вкажи раціональні способи множення числа на 50, на 25, на 15.
7. Віднови цифри, замінені зірочками:

1. *** : ***1 = 9; (909 : 101 або 999 : 111)
2. *43 : *9 = 7. (343 : 49)

ІV. Многокутник. Кут

1. В який із зазначених моментів часу годинна і хвилинна стрілки утворюють гострий ку:

1. 21 год 5 хв;
2. 12 год 15 хв;
3. 13 год 25 хв;
4. 16 год 35 хв;
5. 18 год 50 хв?

2. Скільки тупих кутів зображено на малюнку?

 

 

 

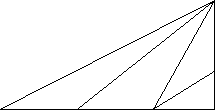
3. Скільки кутів, менших від розгорнутого, зображено на малюнку? Скільки серед них прямих?

 

 

 

 

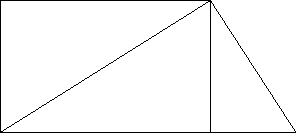
V. Вирази. Нерівності. Рівняння.

1. Склади вираз для обчислення площі прямокутної ділянки, довжина якої – 28 м, а ширина – на х м менша? (28 ∙(28 - х)).
2. Із двох міст назустріч один одному одночасно виїхали два мотоциклісти, які зустрілись через 3 години. Швидкість першого мотоцикліста 60 км/год. Склади вираз для обчислення відстані між цими містами, якщо швидкість другого мотоцикліста на х км,год більша від швидкості першого. (3 ∙ (60 + 60 + х)).
3. При яких натуральних значеннях х справедливі нерівності:

1. 92 – 7х > 43;
2. 36 + х < 42;
3. 92 – 7x > 36 + x?

4. Знайди невідомий доданок і визнач корінь рівняння

3х + 283 = 147 + 394.

Відповідь: 86.

5. Знайди усно корінь рівняння х : 5 = 3625 : 5. (3625)
6. Яка сума коренів таких рівнянь:

8 ∙ 125у = 1000 та 25 ∙ 40у = 2000 (Відповідь: 3).

VI. Коло. Круг Діаграми.

1. Дано прямокутник зі стороною 20 м і квадрат. Периметр кожного з них дорівнює 100 м. Площа якої фігури більша? (Площа квадрата більша).
2. Одну сторону квадрата збільшили на 2 см, а другу зменшили на 2см. Утворився прямокутник. Порівняй площі цих фігур. (Площа квадрата більша).
3.  У колі провели п’ять радіусів: ОА, ОВ, ОС, ОD і ОЕ. Відповідаючи на запитання, скільки при цьому утворилося секторів, Михайлик сказав, що 20. Чи не помилився він? (Не помилився).
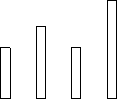
4. Колекція Остапа нараховує 1440 поштових марок на такі теми: комахи, тварини, птахи, автомобілі. Кількість марок на кожну з цих тем зображено на стовпцевій діаграмі (див. мал.). Визнач із точністю до десятків кількість марок на названі теми.

   

 

 

VII. Прямокутний паралелепіпед.

1. Маємо дротяний каркас прямокутного паралелепіпеда, виміри якого дорівнюють 5 см, 10 см і 12 см. Скільки дроту пішло на виготовлення цього каркасу? (108 см).
2. В Олеся був акваріум, в основі якого квадрат зі стороною 28 см. Рівень води в ньому 32 см. Його замінили новим акваріумом, довжина дна якого 32 см, а ширина 28 см. Олесь перелив воду у новий акваріум. Яким став рівень води? (28 см).
3. У басейн із горизонтальним дном площею 1 га залили мільйон літрів води. Чи можна у цьому басейні проводити змагання з плавання? (Не можна, бо глибина басейну 10 м).

VIII. Дробові числа.

1. Назви значення m, при яких дроби   і   одночасно правильні.(6 або 7)
2. Назви ті значення а, при яких дроби    і   одночасно правильні, а дріб   неправильний. (4 або 5)
3. Після того, як пішохід пройшов  шляху і ще 5 км, йому залишилося пройти  частину всього шляху. Скільки кілометрів запланував пройти пішохід? (50 км).
4. Коли велосипедист проїхав 60 км і ще половину всього шляху, то до місця призначення залишилося їхати ще 20 км. Яка довжина всього шляху? (160 км).
5. У вівчаря, який переганяв 60 овець, запитали: «Яку частину отари ти женеш на нове пасовисько?» Він відповів: «Я жену половину від третини отари». Скільки овець у всій отарі? (360 овець).
6. Знайди суму коренів рівнянь: 8,04х = 80 400 і 703 : х = 0,0703 . (20000)
7. Обчисли суму часток 4,26 : 0,71 і 1,74 : 2,9. (6,6).
8. Відстань між двома пунктами 16 км. Визнач масштаб карти, на якій ця відстань дорівнюватиме 32 см. (1 : 50 000).
9. Середнє арифметичне трьох чисел дорівнює 95,549. Знайди перше з цих чисел, якщо друге та третє відповідно дорівнюють 206,08 і 71,56. (9,007).

 

 

 

Задачі на кмітливість

1. У коробці лежать білі, зелені та червоні м’ячики – всього 11 штук. Скільки м’ячиків кожного кольору, якщо зелених у 6 разів більше, ніж червоних? (6 зелених, 1 червоний, 4 білих).
2. Одне яйце варять до готовності протягом 5 хвилин. За скільки хвилин можна зварити 4 яйця? (5 хвилин).
3. П’ять шестиметрових труб розрізають на стовпці довжиною по 2 м. Один розріз триває 3 хвилини. Скільки часу потрібно затратити для виготовлення 15 стовпців? (30 хвилин).
4. Скільки буде десятків, якщо два десятки помножити на 4 десятки? (80 десятків).
5. Двом сестричкам – Оксані та Олі – купили чотири шапочки: три голубі й одну зелену. Дівчатка одягнули нові шапочки до школи. У якій шапочці була Оля, якщо Оксана одягла зелену шапочку? (У голубій).
6. Ігор і Сергій мають прізвища Макар і Кобзар. Які прізвища у цих хлопчиків, якщо у Ігоря чорне волосся, а у Макара – русяве? (Сергій Макар та Ігор Кобзар).
7. Батька вчителя звуть Мирон Петрович, а його сина _ Олександр Тарасович. Як звернутися до вчителя? (Тарас Миронович).
8. У першому таймі футбольного матчу «Нива» вигравала у «Карпат» із рахунком 2:0. Хто переміг у цій грі, остаточний рахунок якої 3:1? («Нива»).
9. На полювання пішли двоє батьків і двоє синів. Вони вбили трьох зайців. Як могло трапитися, що кожний з них приніс додому зайця? (На полюванні були батько, син та онук).
10. У приміському поїзді 6 вагонів. Тарасик сів у четвертий, а Михайлик – у третій вагон. Як могло трапитися, що вони зустрілися в одному вагоні? (Хлопці рахували з різних кінців поїзда).
11. Якщо о 12 годині ночі падає дощ, то чи може бути сонячна погода через 72 години? (Ні, так як буде ніч).
12.  Чи можуть бути істинними твердження:

1. він мені батько, а я йому не син;
2. він мені сусід, але я йому не сусід?

Уроки логічної грамотності

1. Скільки існує натуральних чисел, менших від 100, які:

1. діляться на 2;
2. не діляться на 2;
3. діляться на 3?

Відповідь: 49; 50; 33.

2. Скільки існує натуральних чисел, менших від 100, які:

1. діляться одночасно на 2 і на 3;
2. діляться на 2, але не діляться на 3;
3. діляться на 3, але не діляться на 2.

Відповідь: 16; 49-16 = 33; 33 – 16 = 17.

3. Скільки існує натуральних чисел, менших від 100, які:

1. діляться на 2 або на 3;
2. не діляться ні на 2, ні на 3?

Відповідь: 49 + 33 – 16 = 66; 33.

4. Скільки існує двоцифрових натуральних чисел, менших від 100, цифри яких:

1. ідуть у зростаючому порядку (тобто таких, у яких перша цифра менша за другу);
2. ідуть у спадному порядку;
3. ідуть у не зростаючому порядку?

Відповідь: 36; 45; 54.

Які з вказаних тверджень істинні?

5. Якщо сторони прямокутника 3 і 4 см, то його площа – 12 см². (Істинне)
6. Якщо площа прямокутника 12 см², то його сторони – 3 і 4 см. (Хибне)
7. Якщо сторони прямокутника не дорівнюють відповідно 3 і 4 см, то його площа не дорівнює 12 см². (Хибне)
8. Якщо площа прямокутника не дорівнює 12 см², то його сторони не можуть дорівнювати 3 і 4 см. (Істинне)
9. Якщо кожне з двох чисел більше за 10, то їх сума більша за 20. (Істинне)
10. Якщо сума двох чисел більша за 20, то кожне з цих чисел більше за 10. (Хибне)
11.  Якщо площа прямокутника не збільшилася у 9 разів, то кожна сторона прямокутника не збільшилася у 3 рази. (Істинне)
12. Досліди, як зміниться площа квадрата, якщо його сторони збільшити у 2 рази. (Збільшиться у 4 рази)

 

Використана література

1. Апостолова Г. В., Бакал О. П. Логічними стежинками математики. 5 – 9 класи. К.: Генеза. 2014 р.
2. Гісь Ольга. Яцків Олесь. В країні міркувань. Львів: Світ. 2008 р.
3. Грейміх О. О. Підготовка майбутніх вчителів до міжособистісної професійної взаємодії. К. 2000 р.
4. Енциклопедія освіти. Академія педагогічних наук України; головний редактор В. Г. Кремінь. К.: Юрінком. Інтер. 2008 р.
5. Компетентнісний підхід у сучасній освіті: світовий досвід та українські перспективи. К.: «К. І. С.», 2004 р.
6. Математика. Програма для загальноосвітніх навчальних закладів. Київ. 2016 р.
7. Митник О. Я., Шпак В. І. Народження нестандартного уроку.
8. Педагогічна професія і особистість учителя. Методичні рекомендації. К.: НПУ. 2000 р.
9. Риков С. А. Математична освіта: компетентнісний підхід з використанням ІКТ. Х.: Факт. 2005 р.