Кейс для роботи у профільних класах з математики Тема «Показникова функція. Алгебра 10»
Міський відділ освіти
Навчально-виховний комплекс
«гімназія-школа» № 1
Кейс
для роботи у профільних класах з математики
Тема «Показникова функція. Алгебра 10»
учитель-методист
Акимова Алла Леонідівна
м. Маріуполь, 2019р
П І Б Акимова Алла Леонидівна
посада, предмет учитель математики
педстаж 48 років
освіта вища, Бердянський педагогічний
інститут
кваліфікаційна
категорія спеціаліст вищої категорії ,
учитель- методист
Преамбула
Сучасне замовлення суспільства полягає у тому, щоб забезпечити такі умови навчання, за яких би кожен учень успішно навчався, розвивав свій інтелект, був готовий до творчої самореалізації, щоб створити умови для формування національної свідомості, активної життєвої позиції громадянина – патріота, який може стати активним учасником процесу утвердження незалежності України.
Зміни в освітній політиці відбуваються на основі Державного Стандарту базової і повної середньої освіти і мають на меті формування людини, яка хоче і вміє самостійно вчитися, яка має сприймати інформацію, працювати з інформацією, сортувати її, осмислювати, аналізувати, творити.
Профільне навчання з математики формує у учнів ставлення до навчання як до творчого процесу оволодіння знаннями,засобами їх здобувати, переробляти та застосовувати. Удосконалення математичного навчання неможливо без аналітичної діяльності – моніторингу якості знань учнів.
Моніторинг показує, що учні профільних класів мають міцні, ґрунтовні знання. Результативність навчання можна дослідити по зовнішньому незалежному тестуванню: у 2017 році із 23 учнів, які писали ЗНО – 17 мають достатній і високий рівень (74%).
|
взяли |
від 100 |
від 124 |
від 136 |
від 150.5 |
від 162 |
від 173 |
від 183.5 |
від 190.5 |
від 195.5 |
|
54 |
0 |
0 |
20,37% |
16,67% |
27,78% |
20,37% |
9,26% |
1,85% |
3,75% |
|
учнів |
- |
- |
11 |
9 |
15 |
11 |
5 |
1 |
2 |
Для роботи у профільних класах не завжди достатньо завдань підручника, дидактичних матеріалів. Тому, робота, яка представлена на конкурс є науково-методичним забезпеченням з теми «Показникова функція. Алгебра 10».
Показникова функція, властивості, графік.
І. Тест-контроль «Показникова функція, її графік, властивості»
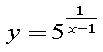 Варіант №1
Варіант №1
- Знайдіть область визначення функціі:
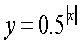
2. Знайдіть множину значень функції:
![]()
3. Побудуйте графік функції:
![]() Варіант № 2
Варіант № 2
- Знайдіть область визначення функціі:
![]()
- Знайдіть множину значень функції:
![]()
- Побудуйте графік функції:
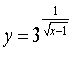 Варіант № 3
Варіант № 3
![]() 1. Знайдіть область визначення функціі:
1. Знайдіть область визначення функціі:
![]() 2. Знайдіть множину значень функції:
2. Знайдіть множину значень функції:
3. Побудуйте графік функції:
![]() Варіант № 4
Варіант № 4
![]() 1. Знайдіть область визначення функціі:
1. Знайдіть область визначення функціі:
2. Знайдіть множину значень функції:
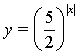 3. Побудуйте графік функції:
3. Побудуйте графік функції:
![]() Зразок виконання ТК № 1(варіант № 4)
Зразок виконання ТК № 1(варіант № 4)
-
; областю визначення функції є всі значення х, для яких
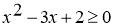 , звідки
, звідки 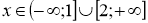 .
.
Отже, ![]() . Відповідь:
. Відповідь: ![]()
-
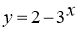 . Оскільки довільна показникові функція набуває лише додатних значень, то для будь-якого
. Оскільки довільна показникові функція набуває лише додатних значень, то для будь-якого 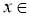 R:
R: 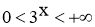 ,
, 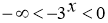 ,
,
![]() , отже
, отже ![]() Відповідь:
Відповідь: ![]()
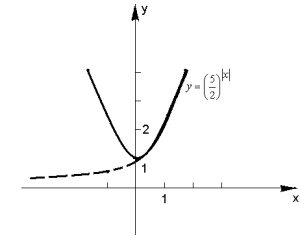 3)
3) 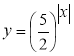
ІІ. Індивідуальні завдання для самостійного виконання
з теми «Показникова функція»
- Знайдіть область визначення функцій :
Відповідь:
а) 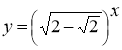 , х є R;
, х є R;
б) ![]() ,
, ![]() ;
;
в) 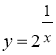 ,
, ![]() ;
;
г) ![]() , х є R;
, х є R;
д) ![]() ,
, ![]() ;
;
е)![]() ,
, ![]() ;
;
є)![]() ,
, ![]() ;
;
- Знайдіть множину значень функції:
Відповідь:
а) ![]() ,
, ![]() ;
;
б) ![]() , у=0;
, у=0;
в) ![]() ,
, ![]() ;
;
г) ![]() ,
, ![]() ;
;
д) ![]() ,
, ![]() ;
;
е) ![]() ,
, ![]() ;
;
ж) ![]() , у=1;
, у=1;
з) ![]() ,
, ![]() ;
;
і) ![]() ,
, 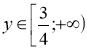
- Побудуйте графік функції:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) 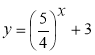 , 4)
, 4) 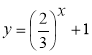 , 5)
, 5) ![]() ,
,
6) ![]() , 7)
, 7) ![]() , 8)
, 8) ![]() , 9)
, 9) 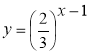 ,
,
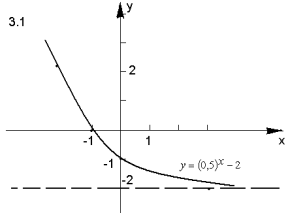
10) ![]() , 11)
, 11) ![]() , 12)
, 12) ![]()
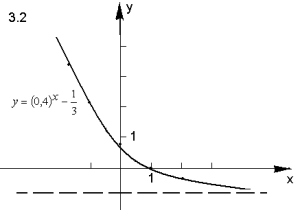 Відповідь.
Відповідь.
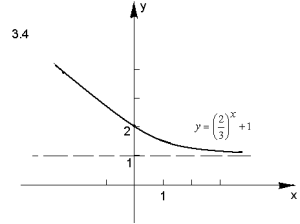
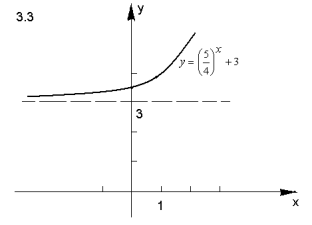
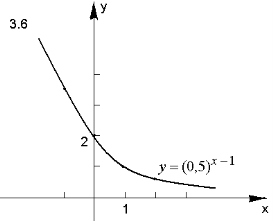
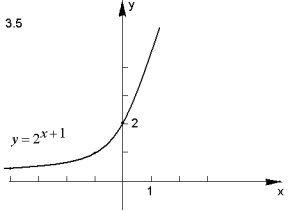
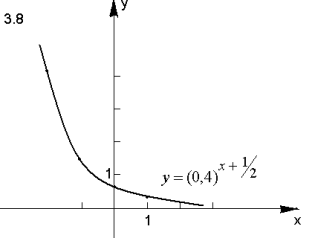
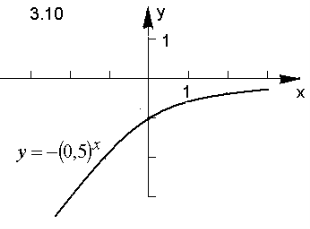
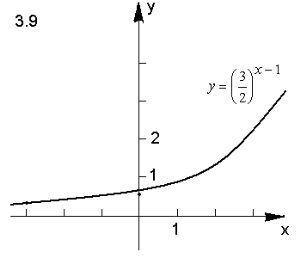
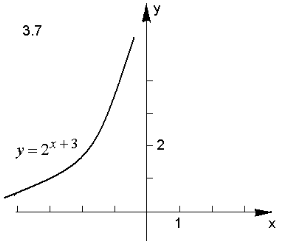
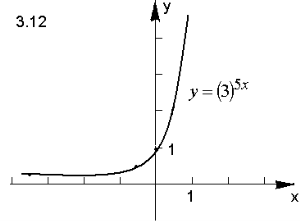
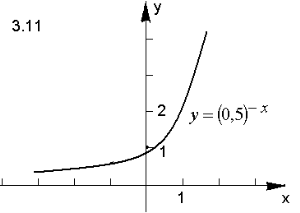
ІІІ. Творчі завдання з теми
“Показникова функція. Побудова графіків функцій”
![]()
![]() Побудувати графік функції:
Побудувати графік функції:
![]() 1) 2) 3)
1) 2) 3)
![]()
![]()
![]()
4) 5) 6)
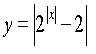
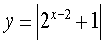
![]()
7) 8) 9)
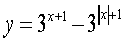
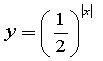
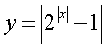
10) 11) 12)
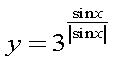
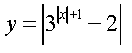
![]()
13) 14) 15)
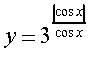
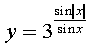
16) 17) ;
IV. Самоосвітня діяльність учнів за опорним конспектом.
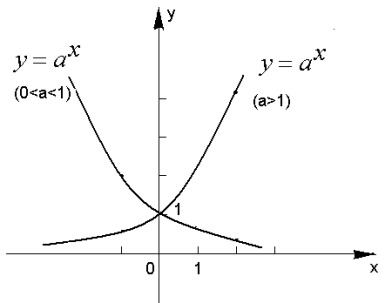
-
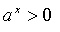 Функція додатна в усій її області визначен- ня, тобто,
Функція додатна в усій її області визначен- ня, тобто,
![]() ,
,
- х>0,
а)![]() , якщо а>0
, якщо а>0
б) ![]() ,якщо 0<a<1
,якщо 0<a<1
- x<0
a) ![]() , якщо а>1
, якщо а>1
б) ![]() , якщо 0<a<1
, якщо 0<a<1
4) Функція ![]() зростає, якщо а>1, і спадає, якщо 0<a<1
зростає, якщо а>1, і спадає, якщо 0<a<1
5) Функція![]() неперервна на інтервалі
неперервна на інтервалі ![]() ,
,
6) Множиною значень функції ![]() є інтервал
є інтервал ![]() , тобто
, тобто ![]() ,
, ![]() .
.
Приклад № 1. Використовуючи властивості показникової функції, виявити зростаюча чи спадаюча функція:
1) ![]()
Рішення.
Основа 4>0, тому функція зростаюча.
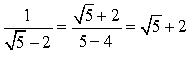 2)
2) 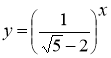
![]() Рішення.
Рішення.
Розглянемо основу функції: , , тому функція 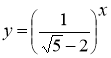 зростаюча.
зростаюча.
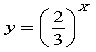
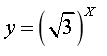 3) Самостійна робота.
3) Самостійна робота.
Вказати зростаючі та спадні функції: а) , б)
![]()
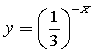
в) ![]() , г) , , д) ;
, г) , , д) ;
Приклад № 2. Порівняти значення виразів, застосовуючи властивості показникової функції
![]()
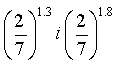
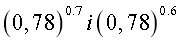
1) ,, 2) , 3) ,
![]()
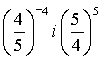
![]()
4) , 5) , 6)
![]()
![]() Рішення.
Рішення.
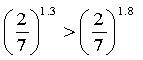 1) , т.я. 3>1 ( -зростаюча)
1) , т.я. 3>1 ( -зростаюча)
2) , т.я. ![]() (
( 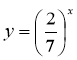 - спадна)
- спадна)
3) ![]() , т.я.
, т.я.![]() (
(![]() - спадна)
- спадна)
4) ![]() , т.я. 2>1 (
, т.я. 2>1 (![]() - зростаюча),
- зростаюча),
5) 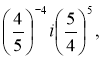
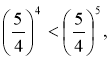 т.я.
т.я. ![]() (
(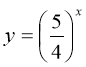 - зростаюча),
- зростаюча),
6) ![]() ,
, ![]() , т.я. 5>1 (
, т.я. 5>1 (![]() - зростаюча).
- зростаюча).
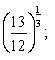
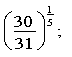 Приклад№3 Порівняти значення виразу з одиницею:
Приклад№3 Порівняти значення виразу з одиницею:
![]()
![]() 1)
1) ![]() 2) 3) 4 ) 5)
2) 3) 4 ) 5)
![]()
![]()
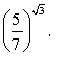
6) 7) 8)
Рішення (зразок)
![]() 1)
1)
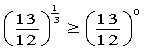
![]()
2) , 3)
![]()
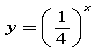 Приклад №4 Побудувати графік функції:
Приклад №4 Побудувати графік функції:
1) , 2)
Рішення
![]()
1)
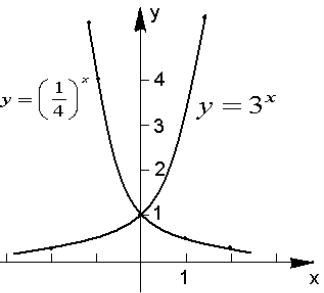
|
х |
-1 |
0 |
1 |
2 |
|
у |
1/3 |
1 |
3 |
9 |
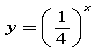
2)
|
х |
-1 |
0 |
1 |
|
у |
4 |
1 |
1/4 |
V. Самоосвітня діяльність учнів. Завдання для дистанційного навчання.
- Порівняти показники m і n, якщо відомо, що нерівність вірна.
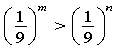
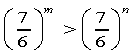
![]() а) , б) , в)
а) , б) , в)
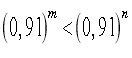
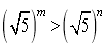
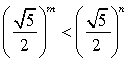
г) , д) ,, е) ,
є) ![]() , ж)
, ж) ![]()
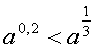 2) Порівняти з одиницею додатну основу а, якщо відомо, що нерівність вірна:
2) Порівняти з одиницею додатну основу а, якщо відомо, що нерівність вірна:
![]()
![]()
![]()
а) , б) ) , ,в) г)
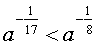
![]()
д) , е)
3) Побудувати графік функйії
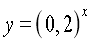
![]()
а) , б)
![]()
![]()
в) , г)
Показникові рівняння
Основні методи розв'язування показникових рівнянь.
(Самоосвітня діяльність учнів за опорним конспектом)
![]()
![]() І.Рівняння виду
І.Рівняння виду
![]()
![]()
![]() Якщо ,то рівняння рівносильне рівнянню У загальному випадку рівняння
Якщо ,то рівняння рівносильне рівнянню У загальному випадку рівняння ![]() рівносильне рівнянню
рівносильне рівнянню
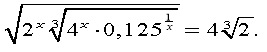 Розв'язати рівняння:
Розв'язати рівняння:
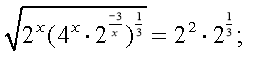 Розв'язання
Розв'язання
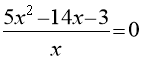
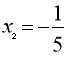
![]()
![]()
![]()
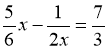
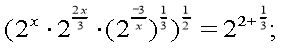 , , ,
, , ,
![]()
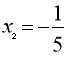
Відповідь: , ;
![]()
ІІ. Рівняння виду
![]()
![]()
Рівняння виду рівосильне рівнянню
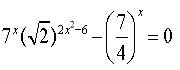
Розв'язати рівняння:
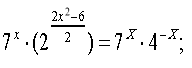 Розв'язання
Розв'язання
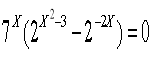
![]()
![]()
![]()
![]()
Відповідь:
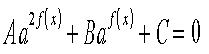
![]()
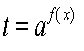 ІІІ. Рівняння виду ,
ІІІ. Рівняння виду ,
![]() Це рівняння розв'язується за допомогою заміни
Це рівняння розв'язується за допомогою заміни
Зазначимо, що .
![]()
Розв'язати рівняння :
![]() Розв'язання
Розв'язання
Помноживши обидві частини рівняння на 5, маємо
![]()
![]()
![]()
![]()
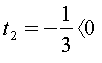
Заміна , . Тоді , ,
![]()
![]()
тоді , .
![]()
Відповідь : .
![]()
![]()
![]()
IV .Рівняння виду
![]() Це рівняння розв'язується за допомогою заміни змінних , t>0 .
Це рівняння розв'язується за допомогою заміни змінних , t>0 .
Розв'язати рівняння: ![]()
Розв'язання.
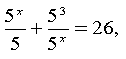
![]()
![]()
![]() , ,
, ,
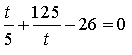
![]()
![]()
![]()
, , ,
![]()
![]()
![]() Звідси,
Звідси, ![]() , , ,
, , ,
![]()
![]()
Відповідь: ,
![]()
V. Заміна у різних рівняннях.
Розв'язати рівняння:
![]() ,
,![]() ,
, ![]()
![]()
,
![]()
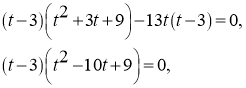
![]() звідти:
звідти:
![]()
Відповідь:
![]()
V I. Рівняння виду
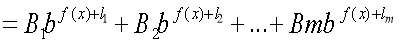
![]()
![]()
Після винесення за дужки в лівій частині , а в правій й
![]()
обчислень дістанемо рівняння
![]()
Поділивши ліву і праву частини на ,
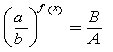
дістаємо
![]()
Розв'язати рівняння:
Розв'язання:
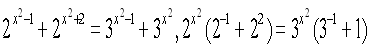
![]()
![]()
. Поділимо ліву і праву частини на
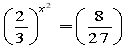
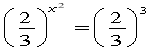
![]()
![]()
Маємо , ; ;
![]()
Відповідь .
VII. Показникові рівняння із взаємно оберненими основами:
![]()
Якщо для рівняння
![]()
виконується умова , то зручною є заміна
![]()
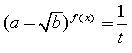
, тоді
![]()
Розв'язати рівняння:
Розв'язання:
![]()
Оскільки ![]() , то позначимо
, то позначимо
тоді 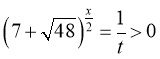 .
.
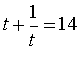
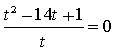
![]()
Маємо , ; .
![]()
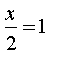 Тобто 1)
Тобто 1) 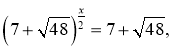 ,, ;
,, ;
![]() 2) ,
2) , 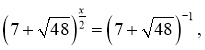
![]()
![]()
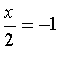
,
![]()
![]() Відповідь: , .
Відповідь: , .
![]()
VIIІ. Рівняння виду .
Таке рівняння розв'язуємо логарифмування (відразу ж або після спрощень), вибираючи зручну основу логарифма.
![]()
Розв'язати рівняння : .
Розв'язання.
![]()
![]()
![]()
Функція має зміст, якщо ,
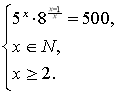 Це рівняння рівносильне системі
Це рівняння рівносильне системі
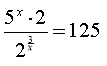
![]()
![]()
, ,
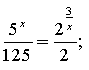
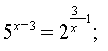
![]()
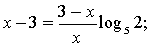
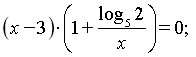 Логарифмуємо це рівняння, наприклад за основою 5 .
Логарифмуємо це рівняння, наприклад за основою 5 .
Дістанемо
![]()
1)x-3=0;
![]()
Відповідь: x=3
ІХ. Однорідні показникові рівняння другого степеня
![]()
- Рівняння виду
є однорідними показниковими рівняннями другого степеня .Метод їх
![]()
розв'язання полягає в діленні лівої і правої частини на
![]()
Тоді маємо
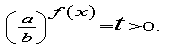
Далі заміна
2)До однорідних показникових рівнянь можна звести рівняння виду
![]()
![]()
![]()
![]() , , якщо .
, , якщо .
Розв'язати рівняння: ![]()
![]()
Розв’язання
![]()
![]()
![]()
поділимо ліву і праву частини рівняння на ,
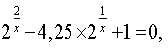
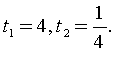
![]() ,
,
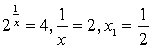
Звідси: 1)
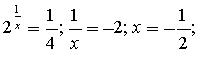
2)
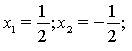
Відповідь:
- Параметри у показниковому рівнянні.
Розв'язати рівняння: ![]()
При яких значеннях a рівняння має розв'язок?
![]() Розв'язання.
Розв'язання.
![]()
![]()
-
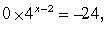 якщо a=3, то рівняння не має розв'язків.
якщо a=3, то рівняння не має розв'язків.
![]()
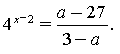
- якщо то Це рівняння матиме розв'язок,
![]()
![]()
якщо тобто У цьому разі
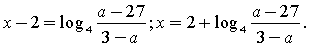
![]()
![]()
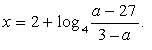
![]() Відповідь: якщо або не має розв'язків,
Відповідь: якщо або не має розв'язків,
якщо то
![]() ХІ. Показникові рівняння + прогресія.
ХІ. Показникові рівняння + прогресія.
Розв'язвти рівняння:
( вираз у правій частині – нескінченна геометрична прогресія).
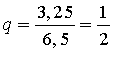
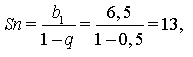 Розв'язання
Розв'язання
Знаменник прогресії , ії сума
![]()
![]()
![]()
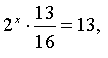
маємо
![]()
Відповідь:
ХІІ . Показниково-тригонометричні рівняння
Розв'язати рівняння: 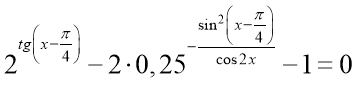
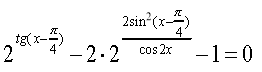 Розв'язання
Розв'язання
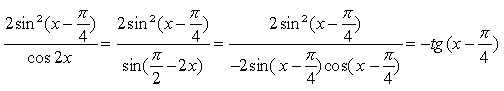
,
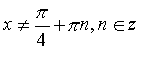
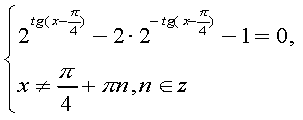
при
Початкове рівняння рівносильне системі :
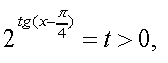
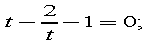
![]()
![]()
![]()
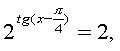
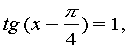
отже
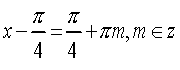
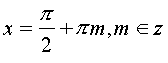
,
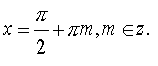 .
.
Відповідь:
XIII . Степенево-показникові рівняння
![]()
Функція виду будемо називати степенево-показниковою. Існує дві точки зору стосовно області визначення функцій :
![]()
![]()
1. , - набуває будь-яких значень.
![]()
![]()
2.Якщо ,то - набуває будь-яких значень.
![]()
![]()
![]()
![]()
Якщо ,то , якщо ,то
набуває цілих значень. Рівняння виду ![]()
назвемо степенево-показниковим.
Дотримуючись першої точки зору,необхідно розглянути два випадки:
![]()
1) ,корені цього рівняння є коренями рівняння ![]()
![]()
якщо значення функцій і ![]()
![]() від цих корнів існують
від цих корнів існують
2)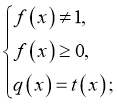
![]() Дотримуючись другої точки зору необхідно розглянути чотири випадки:
Дотримуючись другої точки зору необхідно розглянути чотири випадки:
1) . Корені цього рівняння є коренями рівняння ![]()
![]()
![]()
якщо значення функції і від цих коренів - цілі числа
однакової парності.
![]() 2) Корені цього рівняння є коренями рівняння
2) Корені цього рівняння є коренями рівняння ![]()
![]()
![]()
якщо значення функції і від цих коренів – додатні.
![]()
![]()
![]()
![]() 3) . Корені цього рівняння є коренями рівняння
3) . Корені цього рівняння є коренями рівняння
![]()
![]() якщо значення функції і від цих коренів - існують.
якщо значення функції і від цих коренів - існують.
4) . Корені цього рівняння є коренями рівняння
![]() якщо при значеннях ,що дорівнюють цим кореням, рівняння
якщо при значеннях ,що дорівнюють цим кореням, рівняння
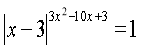
![]() має зміст.
має зміст.
Розв`язати рівняння : .
![]()
![]() Розв`язання.
Розв`язання.
![]() 1) , тобто , . Перевіркою встановлюємо, що
1) , тобто , . Перевіркою встановлюємо, що
![]()
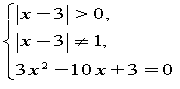
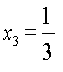 дані числа – корені початкового рівняння.
дані числа – корені початкового рівняння.
2) оскільки , то маємо
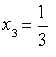
![]()
![]()
Відповідь: , , .
![]()
![]() Примітка. Дотримуючись другої точки зору на область визначення функції
Примітка. Дотримуючись другої точки зору на область визначення функції
дістанемо ті самі корені (зазначимо, що при -ліва
частина рівняння - не визначена).
Творчі завдання з теми «Показникові рівняння» (зразки)
I . Розв'язання показникових рівнянь за допомогою розкладання на множники.
Обираючи спосіб розв'язання показникового рівняння, учні часто забувають про можливість представлення лівої частини рівняння f(x)=0 у вигляді добутку.
![]() Приклад №1. Ров'язати рівняння:
Приклад №1. Ров'язати рівняння:
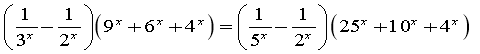 Розв'язання
Розв'язання
,
![]()
,
![]()
![]()
![]() ,
,
, ,
![]()
,
![]()
![]()
![]()
![]()
![]() Звідси, 1) , х=0;
Звідси, 1) , х=0;
2) , оскільки для будь-якого значення х ліва частина додатна
Відповідь: х=0
ІІ. Використання властивостей функцій для розв`язання показникових
рівнянь.
У випадках, коли показникове рівняння не допускає аналітичного розв'язування, застосовують штучні прийоми, пов'язані з використанням властивостей функціі, зокрема монотонності та обмеженості.
![]() Інколи для дослідження функціі використовують похідну. При цьому використовують такі твердження.
Інколи для дослідження функціі використовують похідну. При цьому використовують такі твердження.
![]()
![]() 1) Рівняння ,де і - відповідно зростаюча і
1) Рівняння ,де і - відповідно зростаюча і
![]() спадна на інтервалі(a,b) функціі,має на цьому інтервалі не більш ніж один корінь.
спадна на інтервалі(a,b) функціі,має на цьому інтервалі не більш ніж один корінь.
-
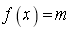
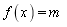 Якщо неперервна функція монотонно зростає (спадає) на інтервалі(a,b), набуваючи значень з ынтервалу(c,d), тоді рівняння
Якщо неперервна функція монотонно зростає (спадає) на інтервалі(a,b), набуваючи значень з ынтервалу(c,d), тоді рівняння
![]()
![]() де m (c,d) на інтервалі(a,b) має один корінь (корінь рівняння
де m (c,d) на інтервалі(a,b) має один корінь (корінь рівняння
![]()
![]() точка ).
точка ).
- Якщо функція та монотонно зростають (спадають)
![]()
на інтервалі (а,b), то сума також зростає (спадає) на (a,b).
![]()
![]()
Зокрема, сума - зростаюча на всій числовій осі функція,якщо ,
![]()
![]()
![]() , і спадна, якщо та . В обох випадках множина
, і спадна, якщо та . В обох випадках множина
значень цієї функції – інтервал ![]() .
.
![]()
Розв'язати рівняння : .
Розв'язання
![]()
Перетворемо рівняння до вигляду
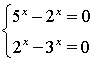 Сума невід’ємних додатків дорівнює 0 тільки тоді, коли кожен доданок дорівнє 0.
Сума невід’ємних додатків дорівнює 0 тільки тоді, коли кожен доданок дорівнє 0.
Отже, рівняння рівносильне системі рівнянь
її розв'язок – x = 0 .
Відповідь : x = 0.
![]() III.Рівняння, в яких основи степенів містять радикали
III.Рівняння, в яких основи степенів містять радикали
Розглянемо рівняння вигляду (1)
![]() Тут задані сталі, причому обов`язково
Тут задані сталі, причому обов`язково
![]()
![]()
![]() Характерна особливість цього рівняння – наявність спряжених виразів
Характерна особливість цього рівняння – наявність спряжених виразів
та . . Нехай d=1, тоді рівняння (1) набуває вигляду
![]()
![]() , подальше розв`язування якого визначається значеннями підкореневих виразів, а саме:
, подальше розв`язування якого визначається значеннями підкореневих виразів, а саме:
![]() 1)Якщо , то після заміни
1)Якщо , то після заміни
![]()
отримують квадратне рівняння .
![]()
![]()
![]() 2)Якщо , то раціоналізація рівняння неможлива. У цьому разі часто застосовують такий прийом «вгадують» корінь рівняння (один або декілька), після чого доводять неможливість існування інших коренів. Нехай у рівнянні (1) .
2)Якщо , то раціоналізація рівняння неможлива. У цьому разі часто застосовують такий прийом «вгадують» корінь рівняння (один або декілька), після чого доводять неможливість існування інших коренів. Нехай у рівнянні (1) .
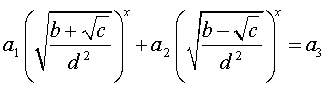 Розділивши обидві частини рівняння на додатний вираз , отримаємо рівносильне рівняння
Розділивши обидві частини рівняння на додатний вираз , отримаємо рівносильне рівняння
.
![]()
![]()
![]()
![]() Тепер зрозуміло,що за умови ,тобто (2) рівняння (1) зводиться до квадратного рівняння. Зазначимо, що в цьому разі (1) є однорідним рівнянням другого степеня відносно та .
Тепер зрозуміло,що за умови ,тобто (2) рівняння (1) зводиться до квадратного рівняння. Зазначимо, що в цьому разі (1) є однорідним рівнянням другого степеня відносно та .
Зауваження. Показникове рівняння
![]() вигляду
вигляду 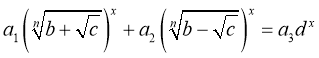 зводиться до квадратного рівняння за умови
зводиться до квадратного рівняння за умови
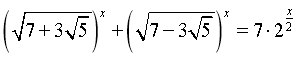
1)Розв`язати рівняння:
Розв'язання
Маємо рівняння вигляду (1) . Перевіримо,чи можна це рівняння
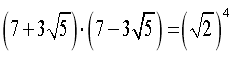
раціоналізувати.Умова (2) виконується: ,
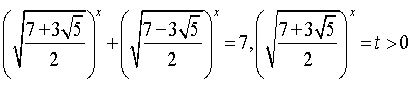
або 4=4,звідси,
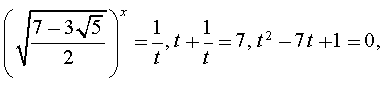
тоді
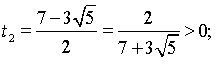
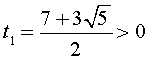
Знайдемо корені вихідного рівняння:
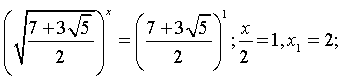
1)
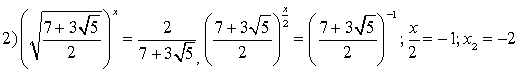
![]()
Відповідь:
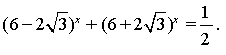
2) Розвязати рівння: Розвязання.
![]()
, звідсі випливає що це рівняння не зво-
![]()
![]()
диться до квадратного. Порівняємо основи з одиницею:
![]() Отже, ліва частина рівння - зростаюча функція на всій числовій осі, графік
Отже, ліва частина рівння - зростаюча функція на всій числовій осі, графік
якої перетинає горизонтальну пряму лише один раз, причому абсциса
![]() спільної точки від’мна. Перевіримо значення Х =-1:
спільної точки від’мна. Перевіримо значення Х =-1:
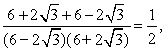
![]()
![]()
![]()
![]()
отже рівняння має єдиний корінь
![]() Відповідь:
Відповідь:
![]() 3)Розв'язати рівняння:
3)Розв'язати рівняння:
![]() Розв'язання.
Розв'язання.
Враховуючи помножимо обидві частини рівняння на
![]()
![]() після чого кількість різних основ зменшиться щонайменше на одну. Оскільки
після чого кількість різних основ зменшиться щонайменше на одну. Оскільки
![]()
![]()
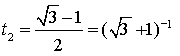 в результаті отримаємо квадратне рівняння
в результаті отримаємо квадратне рівняння ![]() відносно змінної
відносно змінної
![]() або
або
Повернувшись до змінної, маємо:
![]()
![]()
![]() 1)
1)
![]()
![]()
![]() 2) ,
2) ,
Відповідь:
IV . Використання монотонності.
![]() Розглянемо приклади розв'язування рівнянь, степені яких не зводяться до однієї основи.
Розглянемо приклади розв'язування рівнянь, степені яких не зводяться до однієї основи.
Розв'язати рівняння: .
Розв'язання.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Кожен доданок лівої частини рівняння – зростаюча функція, їх сума – також зростаюча функція. Враховуючи сталість правої частини, доходимо висновку, що рівняння може мати не більше, ніж один корінь. Шукаємо корені на множині цілих чисел. Нехай , тоді , отже . Перевіримо : , отже, - корінь рівняння.
Кожен доданок лівої частини рівняння – зростаюча функція, їх сума – також зростаюча функція. Враховуючи сталість правої частини, доходимо висновку, що рівняння може мати не більше, ніж один корінь. Шукаємо корені на множині цілих чисел. Нехай , тоді , отже . Перевіримо : , отже, - корінь рівняння.
Відповідь: .
Міні-підручник «Показникові рівняння»
Розв'язати рівняння: Відповідь:
![]()
1. ![]()
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
5.
![]()
![]()
6.
![]()
![]()
7.
![]()
![]()
8.
![]()
![]()
9.
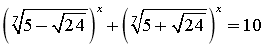
![]()
10.
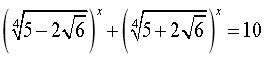
![]()
11.
![]()
![]()
12.
![]()
![]()
13.
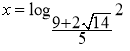
![]()
14.
15. ![]()
Вказівка ![]()
![]() скористуйтесь властивостями
скористуйтесь властивостями
функції ![]() яка при t>1є монотонно
яка при t>1є монотонно
зростаючою. Х=-1; 1.
16. ![]() Х=-1; 1.
Х=-1; 1.
17. ![]()
![]()
18. ![]() х=0
х=0
19. ![]()
![]()
20. ![]()
![]()
21. ![]()
![]()
22. ![]()
![]()
23. ![]()
![]()
24. ![]()
![]()
25. ![]()
![]()
26. ![]()
![]()
27. ![]() x=0,5;
x=0,5;
![]()
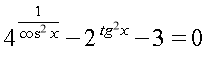 28. x=3;
28. x=3;
![]()
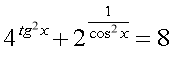 29. x=
29. x= ![]()
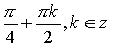
30. x=
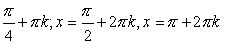
![]()
31. x=
![]()
![]()
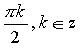
32. x=
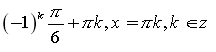 33.
33. 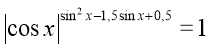 x=
x=
![]()
34. x=1
![]()
35. x=0
![]()
36. x=-4,x=-1
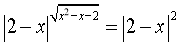
![]()
37. x=-2,x=3
38. x=0
![]()
39.При яких значеннях параметра а
![]()
рівняння
має два дійсні різні корені?
![]() 40.Розв'язати рівняння: 1) ,якщо а=0
40.Розв'язати рівняння: 1) ,якщо а=0
![]()
![]() 2) х=0,якщо а=1
2) х=0,якщо а=1
3) , якщо а<0
![]()
![]() 4)
4)
якщо а>0,
Контрольна робота з теми “Показникові рівняння”
Варіант 1
Розв`язати рівняння: Відповідь:
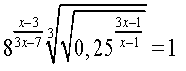
![]() а)
а)
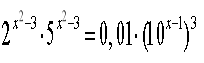
![]()
б)
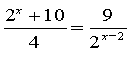
![]()
в)
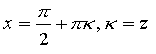
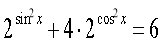
г)
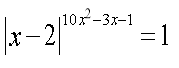
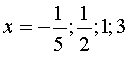
д)
Варіант 2
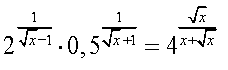 Розв`язати рівняння: Відповідь:
Розв`язати рівняння: Відповідь:
![]() а)
а)
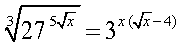
![]() б)
б)
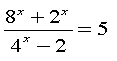
![]()
в)
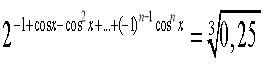
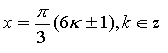
г)
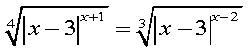
![]()
д)
Варіант 3
Розв`язати рівняння: Відповідь:
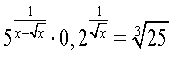
![]()
а)
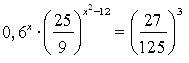
![]()
б)
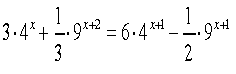
![]()
в)
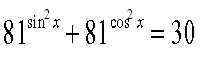
![]()
г)
![]()
![]() д)
д)
Варіант IV.
Розв'язати рівняння:
а)
![]()
б)
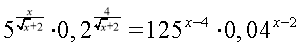
в)
![]()
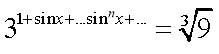
г)
д)
![]()
Зразок рішення IV варіанта
Розв'язати рівняння:
![]()
а)
Розв'язання
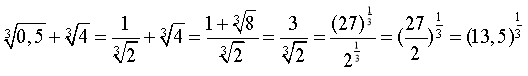
![]()
![]() звідси, початкове рівняння має вигляд:
звідси, початкове рівняння має вигляд:
Відповідь: х = 3.
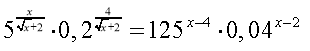 б)
б)
Розв'язання
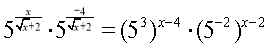
![]() ,
, ![]()
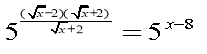
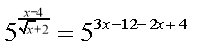
,
![]()
![]()
![]()
, ,
![]()
![]()
,
Відповідь: х = 9.
![]()
в)
Розв'язання
![]()
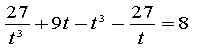
тоді
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: х = 0.
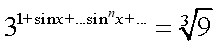
г)
![]()
![]()
![]() Розв'язання
Розв'язання
,оскільки (як сума нескінченно
![]()
![]() спадної геометричної прогресіі з ,і ), звідси,
спадної геометричної прогресіі з ,і ), звідси,
![]()
![]()
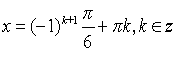
![]() , , ,
, , , ![]()
Відповідь:
![]()
д)
Розв'язання:
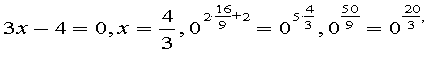
1) ,правильна
![]()
рівність, отже, - корінь рівняння.
![]()
![]()
2) правильна рівність,отже - корінь рівняння.
![]()
3)3х-4=- 1, х=1, - неправильна рівність, отже х=1 – не є коренем рівняння
4) 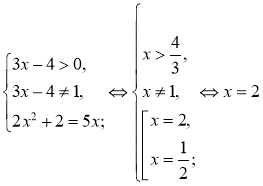
5) 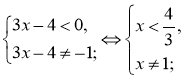
![]()
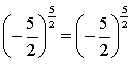 Перевіримо корінь , дістанемо
Перевіримо корінь , дістанемо 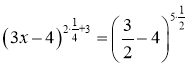
- неправильна рівність ( піднесеня від'ємного числа в
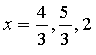 дробовий степінь не має змісту)
дробовий степінь не має змісту)
Відповідь:
Показникові нерівності.
Основні методи розв'язання показникових нерівностей
![]() (самоосвітня діяльність учнів за опорним конспектом).
(самоосвітня діяльність учнів за опорним конспектом).
I. Нерівності вигляду
Рішенія нерівностей грунтується на слідуючих твердженнях:
-
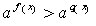
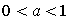
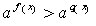 якщо а > 1, то нерівність рівносильна нерівності
якщо а > 1, то нерівність рівносильна нерівності 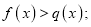
2) якщо , то нерівність рівносильна нерівності![]() .
.
![]()
Розв'язати нерівність:
Розв'язання
![]()
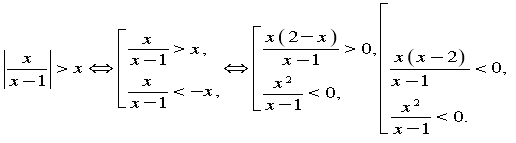 Функція
Функція ![]() спадає , тому
спадає , тому
![]()
![]()
Відповідь:
![]()
ІІ . Нерівність вигляду
![]()
![]() Необхідно розглянути два випадки:
Необхідно розглянути два випадки:
![]()
![]() звідси
звідси
![]() звідси , якщо
звідси , якщо
![]()
![]()
![]() якщо
якщо
![]()
![]()
![]() Якщо , нерівність рівносильне нерівності b<1, якщо
Якщо , нерівність рівносильне нерівності b<1, якщо
![]() Розв'язати нерівність:
Розв'язати нерівність:
![]() Розв'язання.
Розв'язання.
![]()
![]()
![]()
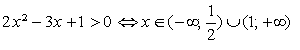 , функція спадає , тому ,
, функція спадає , тому ,
![]()
Відповідь: .
III. Нерівність вигляду ![]()
При розв'язанні нерівності застосовують логарифмування обох частин за основою a або b, враховуючи властивості показниковоі функціі, маємо
![]()
![]() , якщо
, якщо
![]()
![]() , якщо .
, якщо .
![]()
Розвязати нерівність:
Розвязання
Прологарифмуємо обидві частини нерівнрсті за основою 2,
![]()
![]() ,
,
![]()
![]() ,
, ![]()
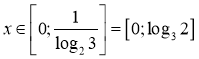
Відповідь:
IV- Заміна змінних у показникових нерівностей
Розв'язати нерівність: ![]()
![]() Розв'язання
Розв'язання
Заміна: ![]() тобто
тобто
![]()
![]()
![]() Маємо ,
Маємо ,
![]()
![]() Тодi
Тодi
![]()
![]()
![]() Відповідь: (0;1) (1;2).
Відповідь: (0;1) (1;2).
V. Розв’язання нерівностей, які містять однорідні функції відносно показникових функцій.
Розв’язати нерівність: ![]()
Розв'язання.
![]() ,
, ![]()
![]()
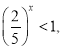
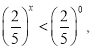
x>0, ![]()
Відповідь: ![]() .
.
Х. Степенево-показникові нерівності.
а) Нерівність вигляду ![]()
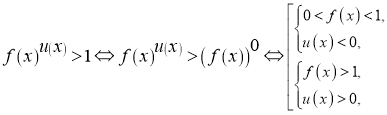
Розв’язати нерівність: ![]()
![]() Розв'язання.
Розв'язання.
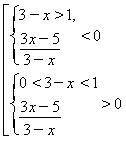
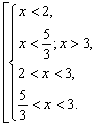
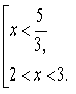
![]()
![]()
![]()
![]()
![]() Відповідь:
Відповідь:
![]() б)Нерівності вигляду
б)Нерівності вигляду
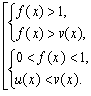
![]()
![]()
![]()
Розв'язати нерівності:
Розв'язання.
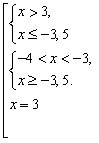
![]()
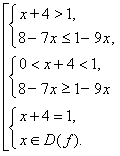
![]()
![]() Д(f) нерівності
Д(f) нерівності
![]()
визначається нерівністю
х+4>0
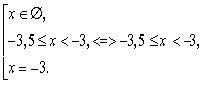
![]()
![]()
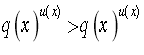 Відповідь: хЄ
Відповідь: хЄ
![]() в) Нерівність вигляду
в) Нерівність вигляду
Розв`язати нерівність:
![]() Розв`язання.
Розв`язання.
Поділимо обидві частини нерівності на
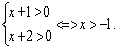
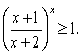
ОДЗ:
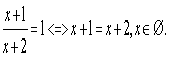
![]()
1)
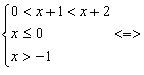
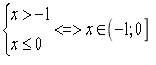
2)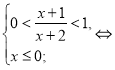
3) 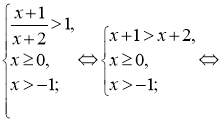
![]()
Звідси, ![]()
Відповідь: ![]()
![]() V. Рішення показникових нерівностей з параметрами
V. Рішення показникових нерівностей з параметрами
1)Розв'язати нерівність:
Розв'зання
Зрозуміло, що а>0.
Розглянемо такі випадки:
![]()
![]() 1)а=1,тоді нерівність розв'зків не має,тобто xє
1)а=1,тоді нерівність розв'зків не має,тобто xє
![]()
![]()
![]() 2)0<а<1.Тоді
2)0<а<1.Тоді
![]() 3) тоді або
3) тоді або
![]()
![]()
![]()
![]() Відповідь: , якщо а=1; , якщо , якщо
Відповідь: , якщо а=1; , якщо , якщо
![]()
2)Указати такі значення X ,при яких нерівність
використовуються для всіх значень Y.
![]() Розв'зання
Розв'зання
Маємо .
Для того щоб ця нерівність виконувалася для всіх значеньY, необхідно вимагати, щоб дискримінант D був від'ємним:
![]()
![]() ,
,
D<0, ![]() ,
, ![]()
![]() Відповідь:
Відповідь:
Міні-підручник. Показникові нерівності
Розв'язати нерівності: Відповідь:
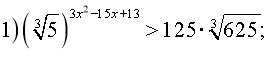
1) ![]()
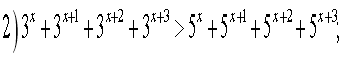
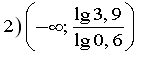
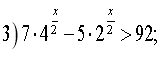
![]()
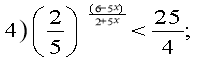
4) ![]()
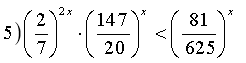
![]()
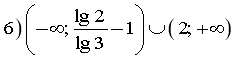
![]()
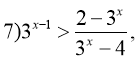
![]()
![]()
![]()
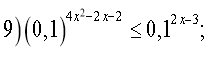
![]()
![]()
![]()
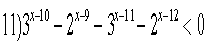
![]()
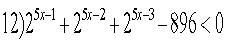
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
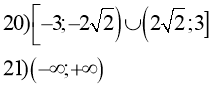
![]()
![]()
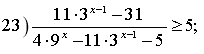
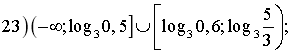
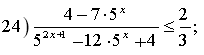
![]()
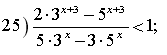
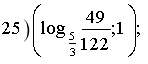
![]()
![]()
![]()
![]()
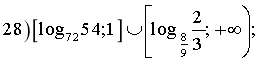
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
34) якщо ![]() ,
,
якщо ![]()
якщо а=1, розв’язків не має;
![]() 35) якщо
35) якщо ![]()
![]()
якщо m>1, ![]()
Контрольна робота з теми «Показникові нерівності»
Варіант№1
Розв'язати нерівність : Відповідь:
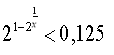
![]()
а)
![]()
![]()
![]() б)
б)![]()
![]() в)
в)
![]() г)
г)
![]()
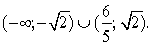
д)
Вариант №2.
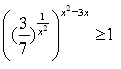 Розв`язати нерівність: Відповідь:
Розв`язати нерівність: Відповідь:
![]()
а)
![]()
![]()
б)
![]()
![]()
в)
![]()
![]() г)
г)
![]()
![]()
д) х![]()
Варіант №3
![]() Розв'язати нерівність: Відповідь:
Розв'язати нерівність: Відповідь:
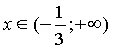
а)
![]()
![]()
б)
![]()
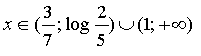 в)
в) ![]()
![]()
г)
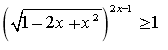
д) ![]()
Варіант № 4
Розв'язати нерівність
![]()
а)
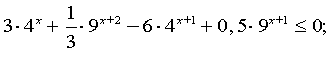
б)
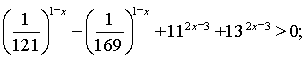
в)
![]()
г)
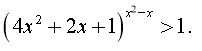
д)
Зразок розв'язання завдань 4 варіанту
![]()
а)Розв'язати нерівність:
Розв'язання
![]() ,
, ![]() ,
, ![]()
дістанемо 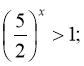
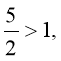 тоді х>0.
тоді х>0.
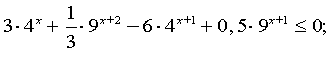 Відповідь:
Відповідь: ![]() .
.
б)Розв'язати нерівність:
Розв'язання
![]()
![]()
![]()
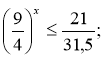
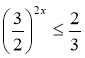 ,
, ![]()
![]()
Відповідь: ![]()
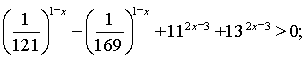 в)Розв'язати нерівність:
в)Розв'язати нерівність:
Розв'язання
![]()
![]()
![]()
![]()
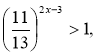
![]()
![]()
Відповідь: ![]()
![]()
г) Розв'язати нерівність:
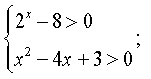
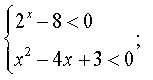 Розв'язання
Розв'язання
а) або б)
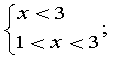
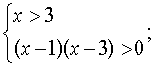
або
![]()
![]()
![]() або
або
Отже,
![]() Відповідь:
Відповідь:
![]()
д) Розв'язати нерівність:
Розв'язання
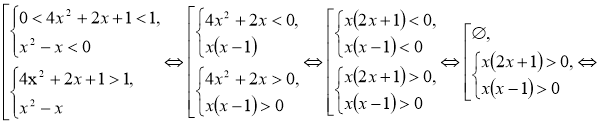
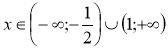
Відповідь: 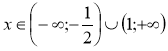
Системи показникових рівнянь. Методи розв’язання систем показникових рівнянь.
І. Метод розв’язання систем рівнянь, з яких одне рівняння – показникове, інше – алгебраічне.
Розв’язати систему рівнянь: 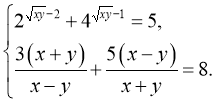
Розв’язання
Заміна: ![]() Тоді із першого рівняння дістаємо
Тоді із першого рівняння дістаємо ![]()
![]() враховуючи t>0. Тобто,
враховуючи t>0. Тобто, ![]() xy=4.
xy=4.
Ще заміна: 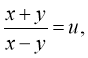 тоді із другого рівняння початкової системи:
тоді із другого рівняння початкової системи:
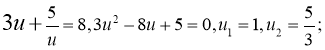 Маємо:
Маємо:
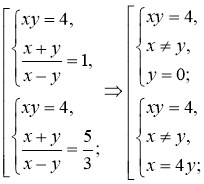
![]()
![]()
![]()
![]()
![]()
![]()
Перша ![]() із систем сукупності розв’язків не має. Розв’язуючи другу, дістаємо:
із систем сукупності розв’язків не має. Розв’язуючи другу, дістаємо: 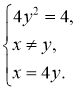 звідси:
звідси: ![]()
Відповідь: ![]()
ІІ. Метод розв’язання систем рівнянь, якщо обидва рівняння системи – показникові.
Розв’язати систему рівнянь: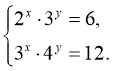
Розв’язання
Логарифмуючи перше рівняння за основою 2, а друге – за основою 3, дістанемо: 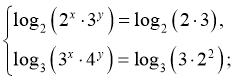
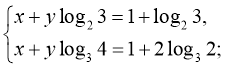
Віднімаючи від першого рівняння друге, маємо
![]() Оскільки
Оскільки ![]() то у=1. Тоді
то у=1. Тоді ![]() х=1.
х=1.
Відповідь: (1;1).
ІІІ. Метод розв’язання систем рівнянь, якщо одне рівняння – показникове, інше – показниково – степеневе.
Розв’язати систему рівнянь: 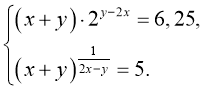
Розв’язання
Заміна: х+у=t, y-2x=z Прологарифмуємо ці рівняння за основою 2:
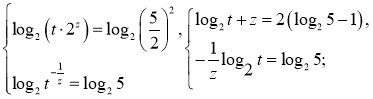
![]()
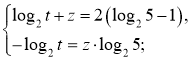 додавши перші два рівняння, дістанемо
додавши перші два рівняння, дістанемо
![]()
![]() оскільки
оскільки ![]() то маємо
то маємо 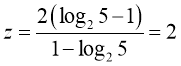 Тоді
Тоді ![]()
![]()
Маємо 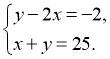
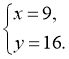
Відповідь: (9;16).
ІV. Метод розв’язання систем рівнянь, якщо одне рівняння – показниково – степеневе, інше – алгебраїчне.
Розв’язати систему рівнянь: 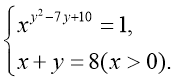
Розв’язання
Розглядаючи перше рівняння, маємо два випадки:
- х=1,
- у2-7у+10=0. Тоді початкова система рівносильна сукупності:
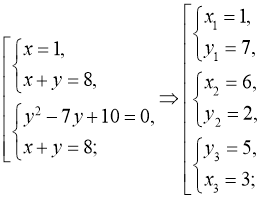
Відповідь: (1;7), (6;2), (3;5).
V. Метод розв’язання систем рівнянь, якщо обидва рівняння системи – показниково – степеневі.
Розв’язати систему рівнянь: 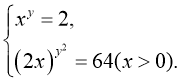
Розв’язання
Логарифмуючи обидва рівняння за основою 2, маємо:
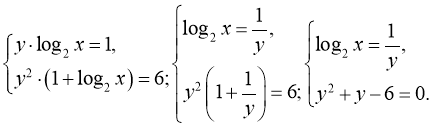
Тоді 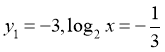 і
і 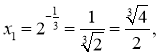
або 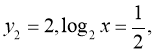
![]()
Відповідь: 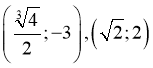
VІ. Метод розв’язання систем рівнянь, якщо одне рівняння системи – показникове, інше – логарифмічне.
Розв’язати систему рівнянь: 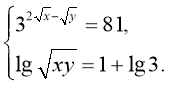
Розв’язання
Маємо: 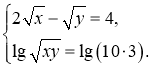 Оскільки х>0 і у>0, то
Оскільки х>0 і у>0, то ![]()
тому 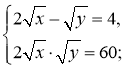
Заміна: ![]() Тоді
Тоді 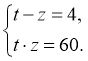 Враховуючи обмеження для t і z, дістаємо
Враховуючи обмеження для t і z, дістаємо ![]() тоді
тоді ![]() і х=25,
і х=25,
![]() і у=36,
і у=36,
Відповідь: (25;36).
VІІ. Метод розв’язання систем рівнянь, якщо одне рівняння системи – логарифмічне, інше - показниково – степеневе.
Розв’язати систему рівнянь: 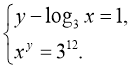
Розв’язання
Логарифмуючи друге рівняння за основою 3(враховуючи додатність лівої частини рівняння), дістанемо: ![]()
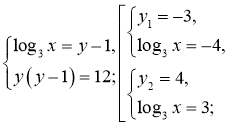
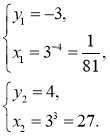
Відповідь: 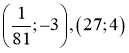
Міні-підручник.
Рішення систем показникових рівнянь.
Розв’язати системи рівнянь. Відповідь.
1) 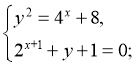 (0;-3)
(0;-3)
2) 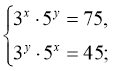 (1;2)
(1;2)
3) 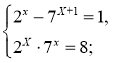 (3;0)
(3;0)
4)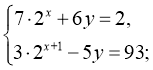 (3;-9)
(3;-9)
5) 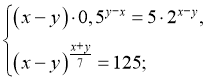 (13;8)
(13;8)
6) 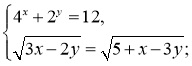 (1,5;2)
(1,5;2)
7) 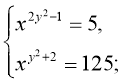 (5;1) і (5;-1)
(5;1) і (5;-1)
8) 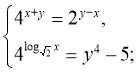 (0,5;-1,5)
(0,5;-1,5)
9) 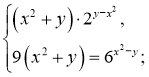
![]()
10)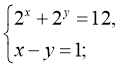 (3;2)
(3;2)
11)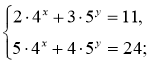 (0;1)
(0;1)
12)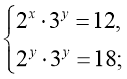 (2;1)
(2;1)
13) 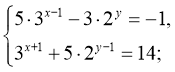 (1;1)
(1;1)
14) 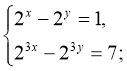 (0;1)
(0;1)
15) 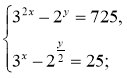 (3;2)
(3;2)
16) 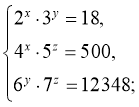 (1;2;3)
(1;2;3)
17) 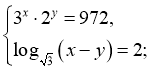 (5;2)
(5;2)
18) 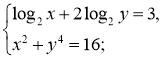
![]()
19) 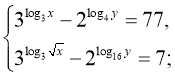 (81;16)
(81;16)
20) 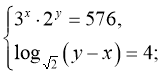 (2;6)
(2;6)
21) 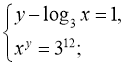
![]()
22) 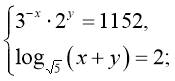 (-2;7)
(-2;7)
23) 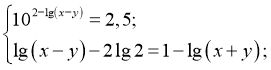 (20,5;-19,5)
(20,5;-19,5)
24) 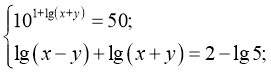 (4,5;0,5)
(4,5;0,5)
25) 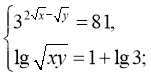 (25;36)
(25;36)
26) 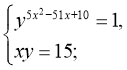
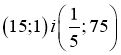 і (10;15)
і (10;15)
27) 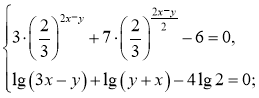 (2;2)
(2;2)
28) 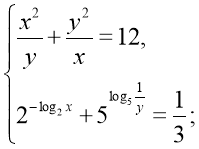 (6;6)
(6;6)
29) 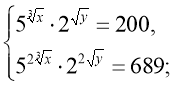 (8;9)і
(8;9)і![]()
30) 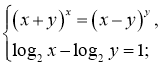
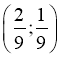
31) 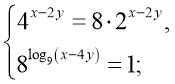 (5;1)
(5;1)
32) 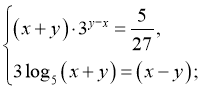
![]() (4;1)
(4;1)
33) Скільки розв’язків мають системи рівнянь в залежності від значень параметра а?
а)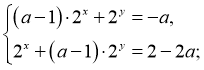 відповідь: якщо
відповідь: якщо ![]() , то 1 розв’язок , якщо
, то 1 розв’язок , якщо![]() , то розв’язки відсутні.
, то розв’язки відсутні.![]()
б) 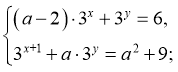 відповідь: якщо
відповідь: якщо ![]() , то 1 розв’язок , якщо а=3, то безліч розв’язків; якщо
, то 1 розв’язок , якщо а=3, то безліч розв’язків; якщо ![]() , то розв’язки відсутні.
, то розв’язки відсутні.![]()
34) Розв’яжіть систему рівнянь за умови, що x>0, y>0.
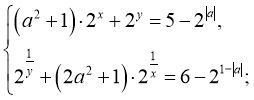 відповідь: х=у=1, якщо а=0,
відповідь: х=у=1, якщо а=0,
додаткових розв’язків не icнує, якщо ![]() .
.
Контрольна робота з теми
«Рішення систем показникових рівнянь»
Варіант №1.
Розв’язати систему показникових рівнянь. Відповідь
а) 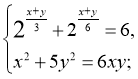 (3;3), (5;1)
(3;3), (5;1)
б) 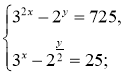 (3;2),
(3;2),
в) 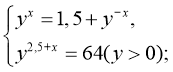
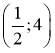
г) 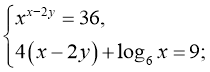 (6;2)
(6;2)
Варіант № 2
Розв’язати систему показникових рівнянь. Відповідь
а) 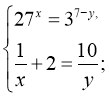 (-1;10),
(-1;10), 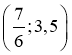
б) 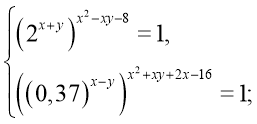 (0;0), (8;-8),
(0;0), (8;-8), 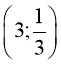 , (-4;-2)
, (-4;-2)
в) 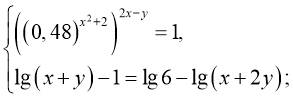 (2;4)
(2;4)
г) 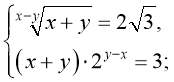 (7;5)
(7;5)
Варіант № 3
Розв’язати систему показникових рівнянь. Відповідь
а) 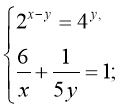 (6;6), (2;2)
(6;6), (2;2)
б) 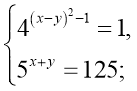 (1;2), (2;1)
(1;2), (2;1)
в) 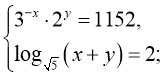 (-2;7)
(-2;7)
г) 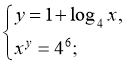 (16;3),
(16;3), 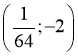
Варіант № 4
Розв’язати систему показникових рівнянь. Відповідь
а) 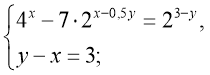 (1;4)
(1;4)
б)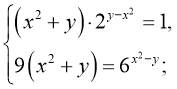
![]()
в)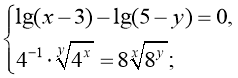 (4;2)
(4;2)
г) 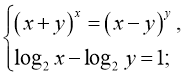
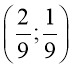
Зразок рішення варіанту № 4
Розв’язати систему показникових рівнянь а) 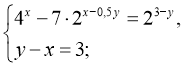
Розв’язання.
Із другого рівняння системи маємо х=y-3. Підставимо це значення в перше рівняння: ![]()
![]()
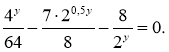 Помноживши ліву і праву частини на
Помноживши ліву і праву частини на ![]()
![]()
дістанемо ![]() заміна:
заміна: ![]()
маємо ![]()
Звідси t= 64 (враховуючи t>0). Тоді 1,5y=6; y=4, x=4-3=1.
Відповідь: (1;4).
б)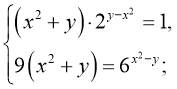
Розв’язання.
Маємо 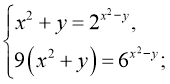 Поділивши почленно друге рівняння на перше, дістанемо
Поділивши почленно друге рівняння на перше, дістанемо ![]() і
і ![]() . Тоді із першого рівняння маємо
. Тоді із першого рівняння маємо ![]() Отже:
Отже:
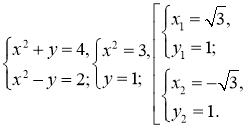 Відповідь:
Відповідь: ![]()
в)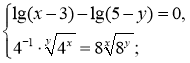
Розв’язання.
Із першого рівняння дістанемо ![]() що рівносильно системі
що рівносильно системі 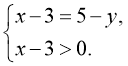 Із другого маємо:
Із другого маємо: 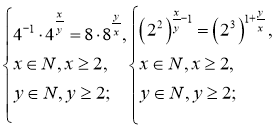
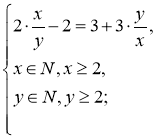
Заміна: 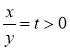 . Тоді
. Тоді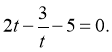 Враховуючи обмеження для t, маємо
Враховуючи обмеження для t, маємо 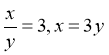 . Отже, початкова система рівносильна такій:
. Отже, початкова система рівносильна такій: 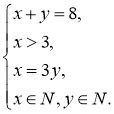
Звідси у=2, х=6.
Відповідь: (6;2)
г) 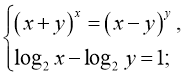
Розв’язання.
При x>0, y>0 із другого рівняння дістанемо: 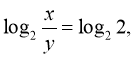 x=2y.
x=2y.
Підставляючи в перше, маємо: ![]()
![]()
![]() Поділимо на
Поділимо на ![]() Дістанемо
Дістанемо ![]()
![]() Оскільки y>0, то єдина можливість 9y=1,
Оскільки y>0, то єдина можливість 9y=1, ![]() Тоді
Тоді 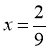 .
.
Відповідь: 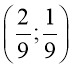
Тематичний тест № 1
« Показникова функція».
І варіант
Рівень А.
-
Знайдіть множину значень функції
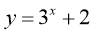
Відповідь: а) ![]() б)
б) ![]() в)
в) ![]() г)
г)![]()
2. Розв’яжіть рівняння: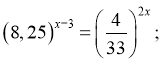
Відповідь: а)-1, б) 1, в)-4, г) -2.
3. На якому з наведених проміжків функція ![]() більша за одиницю?
більша за одиницю?
Відповідь: а) ![]() б)
б)![]() в)
в) ![]() г)
г)![]() д) такого
д) такого
проміжку не існує;
4. Яке з наведених чисел менше за одиницю?
Відповідь: а)![]() б)
б)![]() в)
в)![]() г)
г)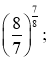 д) жодного з
д) жодного з
наведених;
5. Розв’яжіть рівняння: ![]()
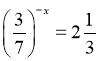
Відповідь: а)-1, б) 2, в) 1, г) 1 і 2, д) ![]()
![]()
6. Укажіть проміжок, якому належіть корінь рівняння ![]()
Відповідь: а) 0, б) 6,4 в) (4; 6] г) [-7; 0), д)(6;7]
7. Упорядкуйте числа за зростанням ![]()
![]()
![]()
Відповідь: а) a<c<b; б) c<b<a в) b<c<a г) a<b<c д) b<a<c
8. Скільки коренів має рівняння: ![]() ?
?
Відповідь: а) жодного, б) один, в) два, г) три, д) більше трьох;
9. Задано рівняння![]() . Знайдіть значення виразу
. Знайдіть значення виразу ![]() де
де
![]() - корені цього рівняння.
- корені цього рівняння.
Відповідь: а) 6, б) -6, в) 5, г) -5, д) 49.
10. Укажіть рівняння, яке має корені.
Відповідь: а)![]() б)
б) ![]() в)
в)![]() г)
г)![]() д) всі наведенні
д) всі наведенні
рівняння мають корені,
11. Знайдіть найбільший цілий розв’язок нерівності ![]()
![]()
Відповідь: а)-2, б) -1, в) 0, г) 1, д) найбільшого розв’язку не існує,
12. Знайдіть область визначення функції 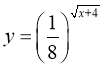
Відповідь: а) ![]() б)
б)![]() в)
в) ![]() г)
г) ![]() д)
д)![]()
13. Розв’яжіть нерівність:![]()
Відповідь: а) (0;0,5) б)![]() в)
в)![]() ,г)[0;0,5],
,г)[0;0,5],
д) ![]()
14. Знайдіть добуток коренів рівняння ![]()
![]()
Відповідь: а) 10, б) -7, в) 7, г) 12, д) -10.
15. Розв’яжіть нерівність: 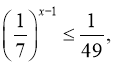
Відповідь: а)![]() б)
б) ![]() в)
в)![]() г)
г)![]() д)
д)![]()
16. Розв’яжіть нерівність:![]()
Відповідь: а) ![]() , б)
, б) ![]() в)
в) ![]() , г)
, г)![]() , д)
, д)![]()
17. Знайдіть добуток коренів рівняння: 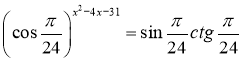
Відповідь: а) 32, б) -32, в) 4, г) -30, д) 30;
18. Розв’яжіть нерівність: 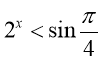
Відповідь: а)![]() , б)
, б)![]() , в)
, в)![]() , г)
, г)![]() , д)
, д)![]()
19. Обчисліть ![]() , якщо
, якщо ![]() - розв’язок системи рівнянь
- розв’язок системи рівнянь 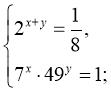
![]()
Відповідь: а) 0, б) 18, в) -18, г) -28, д) -2
20. Укажіть проміжок, який не містить коренів рівняння ![]()
Відповідь: а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)рівняння не має
, д)рівняння не має
коренів
Рівень Б.
21. Знайдіть суму квадратів коренів рівняння ![]()
22. Розв’яжіть рівняння: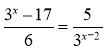
23. Визначте найменший цілий розв’язок нерівності ![]()
24. Визначте суму цілих розв’язків нерівності![]()
25. Визначте найбільший цілий розв’язок нерівності
![]()
26. Визначте найменше значення х, якщо (x,y) - розв’язок системи рівнянь
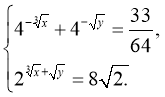
27. Розв’яжіть нерівність 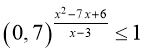 . У відповіді запишіть найменше
. У відповіді запишіть найменше
ціле значення х, яке задовольняє нерівність.
28. Визначте найбільший розв’язок рівняння
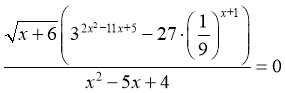
29. Визначте найбільший цілий розв’язок нерівності
![]()
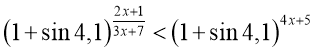
30. Знайдіть х-у, якщо (х;у) - розв’язок системи рівнянь 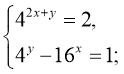
31. Знайдіть найбільше значення функції ![]()
32. Знайдіть кількість коренів рівняння
![]() які належать інтервалу (0;20).
які належать інтервалу (0;20).
ІІ варіант
Рівень А.
1. Укажіть проміжок, на якому функція ![]() від’ємна
від’ємна
Відповідь: а) ![]() б)
б) ![]() , в)
, в)![]() , г)
, г)![]() д)
д) ![]()
2. Яке з наведених чисел більше за одиницю?
Відповідь: а)![]() , б)
, б)![]() , в)
, в) ![]() , г)
, г)![]() , д)
, д) ![]()
3. Обчисліть: 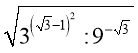
Відповідь: а)![]() , б) 3, в) 9, г)
, б) 3, в) 9, г) ![]() ,
,
4. Розв’яжіть рівняння 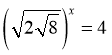
Відповідь: а)1, б) ![]() в) 0,8 г) 1,2 д) 1,6
в) 0,8 г) 1,2 д) 1,6
5. Знайдіть довжину інтервалу, який є розв’язком нерівності ![]()
Відповідь: а) 7, б) 1, в)![]() , г)
, г) ![]() , д)
, д) ![]()
6. Розв’яжіть рівняння 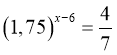
Відповідь: а) 5, б) -7, в) -5, г) 6,5 д) 7
7. Укажіть проміжок, якому належить корінь рівняння 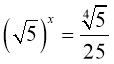
Відповідь: а) ![]() б)
б)![]() в)
в) ![]() г)
г) ![]() д)
д)![]()
8. Знайдіть суму коренів рівняння 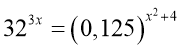
Відповідь: а) 5, б) 4, в) 15, г) -3, д) -5.
9. Розв’яжіть нерівність 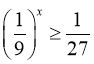
Відповідь: а)![]() б)
б)![]() в)
в)![]() г)
г) ![]() д)
д)![]()
10. Розв’яжіть нерівність 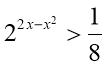
Відповідь: а)![]() б)
б)![]() , в)
, в) ![]() г)
г) ![]()
д)![]()
11. Серед наведених укажіть усі нерівності, які не мають розв’язків:
І. ![]() ІІ.
ІІ. ![]() ІІІ.
ІІІ. ![]() IV.
IV. ![]()
Відповідь: а) I, IIІ б)I,II,IV в) II, IV г) II д) I, II
12. Обчисліть х+у, якщо (х;у) – розв’язок системи рівнянь 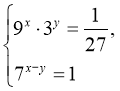
Відповідь: а) -2, б) 2, в)![]() г)
г) ![]() д) 0
д) 0
13. Знайдіть суму коренів рівняння 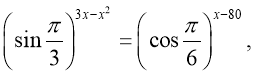
Відповідь: а) -2, б) 2, в) -80, г) 4, д) -4.
14. Розв’яжіть рівняння 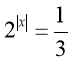
Відповідь: а) 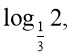 б)
б) 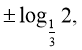 в)
в)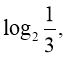 г)
г) 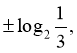 д)
д) ![]()
15. Знайдіть множину значень функції ![]()
Відповідь: а)![]() ,б)
,б) ![]() , в)
, в)![]() ,г)
,г)![]() ,д)
,д)![]()
16. Знайдіть область визначення функції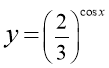
Відповідь: а)![]() , б)
, б) ![]() , в)
, в)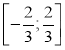 , г)
, г) ![]()
17. Знайдіть суму цілих розв’язків нерівності 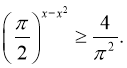
Відповідь: а) 0, б) 1, в) 2, г) 3
18. Розв’яжіть нерівність 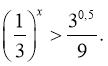
Відповідь: а) ![]() б)
б)![]() в)
в)![]() ,г)
,г)![]()
д)![]()
![]()
19. Розв’яжіть рівняння ![]()
Відповідь: а) o,25, б) -3, в) 4, г) 3
20. Обчислити: 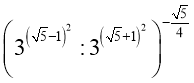
Відповідь: а)![]() , б) 3, в)
, б) 3, в) ![]() , г) 243, д)
, г) 243, д) ![]()
Рівень Б.
21. Визначте найменший цілий розв’язок нерівності ![]()
22. Розв’яжіть рівняння ![]()
23. Визначте суму цілих розв’язків нерівності ![]()
24. Знайдіть х+у, якщо (х;у) - розв’язок системи рівнянь
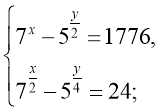
![]()
25. Визначте добуток розв’язків рівняння
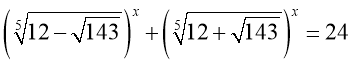
26. Визначте найбільший розв’язок нерівності
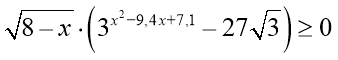
27. Розв’яжіть рівняння ![]()
28. Знайдіть наименший розв’язок рівняння
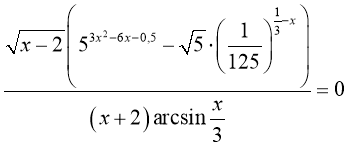
29. Обчислить ![]() , якщо (х;у) - розв’язок системи рівнянь
, якщо (х;у) - розв’язок системи рівнянь
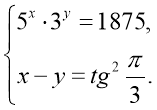
30. Розв’яжіть нерівність 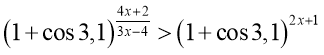
31. Знайдіть найбільше і найменше значення функції ![]()
32. Розв’яжіть систему рівнянь 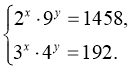
Відповіді до тестових завдань
І варіант.
Рівень А.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
в |
б |
а |
в |
в |
д |
а |
в |
а |
в |
б |
в |
г |
а |
г |
а |
б |
а |
в |
г |
Рівень Б.
![]()
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
|
|
2 |
3 |
2 |
3 |
3 |
0,125 |
1 |
0,5 |
-3 |
-0,5 |
|
7 |
ІІ варіант.
Рівень А.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
д |
г |
в |
д |
б |
а |
в |
д |
г |
г |
в |
а |
б |
д |
г |
г |
в |
в |
а |
г |
Рівень Б.
![]()
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
|
2 |
4 |
2 |
12 |
-25 |
0,4 |
1 |
2 |
4 |
|
25,1 |
(1;3) |
Література
- Бондаренко М.Ф. Математика для вступників до вузів /Х. : Компанія Сміт, 2002. - 1118 с.
- Сканави М.И. Сборник задач по математике /К. : Каннон, 1997. – 528 с.
- Титаренко А.М. Математика /Х. : Мир детства ,2005.- 340 с.
- Саакян С.М. Задачи по алгебре и началам анализа /М. : Просвещение, 1990. - 207 с.
- Симонов Л.Я. Система тренировочных задач и упражнений /М. : Просвещение , 1991. - 207 с.
- Шкіль М.І. Алгебра і початки аналізу 10 клас /К. : Освіта, 2003. - 318 с.
- Нелин В.П. Алгебра и начала анализа 10 класс /Х. : Мир детства, 2006. - 445 с.
- Журналы Математика в школах Украины
№11 – 2009г.. стр. 18-22.
№4 – 2009г., стр. 22-27.
№7-8 – 2009г., стр. 20-27
- Захарійченко Ю.О. Математика /К. : Видавничий дім «Київо-Могилянська академія» ,2007. - 204 с.
1


про публікацію авторської розробки
Додати розробку
