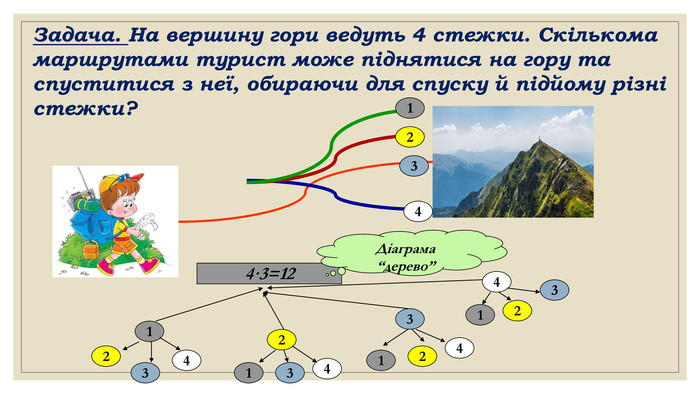
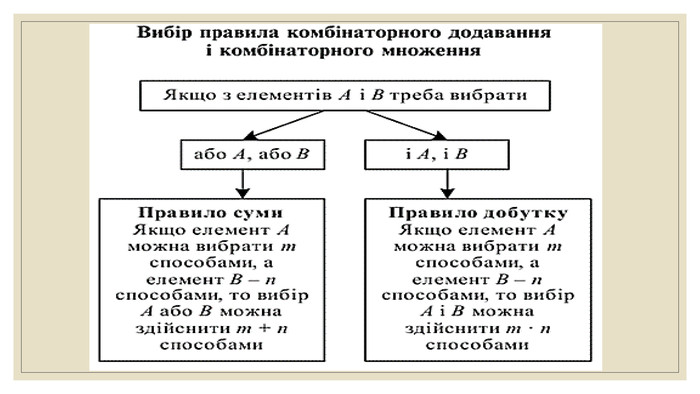
Комбінаторика та правила суми і добутку.
Про матеріал
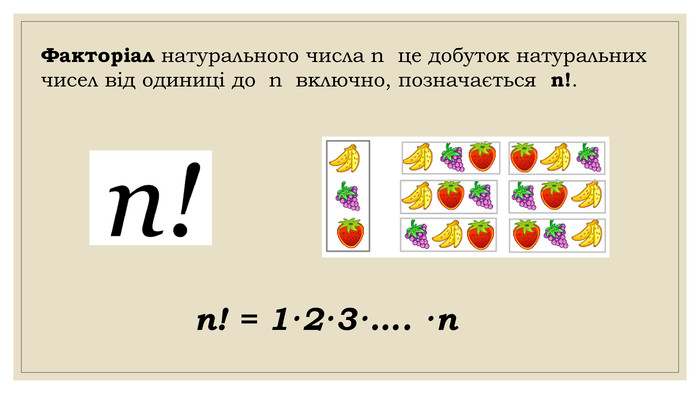
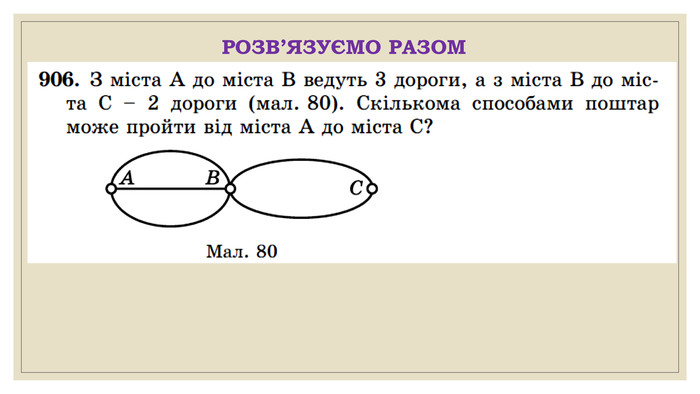
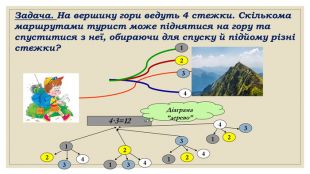
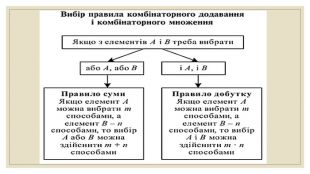
Презентація за темою "Комбінаторика та правила суми і добутку. " Матеріал містить базові поняття комбінаторики, завдання на правило суми та добутку. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 9 клас (Істер О. С.)
До уроку
§ 21. Комбінаторні задачі. Комбінаторні правила суми і добутку Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку