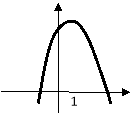
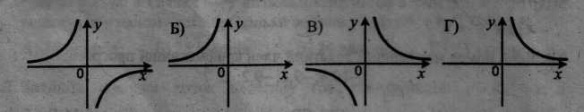Контрольна робота на тему "Функція. Властивості функції" 9 клас алгебра
|
Контрольна робота 9 клас алгебра «Функція. Властивості функції» |
||||
|
Початковий рівень |
||||
|
|
||||
|
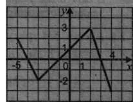
А) [-5; 3]; |
Б) (-5; 3); |
В) [-5; 3] |
Г) (-5;3) |
|
|
||||
|
А) [-3; 3]; |
Б) [-2; 3]; |
В) [-3,5; 1]; |
Г)[-1;4]. |
|
рисунок. А) Б) В) Г)
|
||||
|
||||
|
Б) |
B) -8 |
Г) |
|
|
||||
|
А) [-1; 3]; |
Б) [-2; 2]; |
В) [1; 3]; |
Г) [-2; 1]. |
|
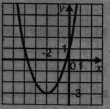
у = f(х), визначеної на проміжку [-3,5;5].
проміжок спадання функції.
|
||||
|
А) |
Б) |
В) [2.5;1] |
Г) |
|
- Установіть відповідність між функцією (1-4) та її властивістю (А-Д).
|
1 |
|
А |
Нулі функції дорівнюють -3 і 0 |
|
2 |
|
Б |
Область визначення функції — (- |
|
3 |
|
В |
Графік функції проходить через точку (0;3) |
|
4 |
|
Г |
Нулі функції дорівнюють -3 і 3 |
|
|
Д |
Область значень функції— [0;+ |
|
- Побудуйте на одній координатній площині графіки функцій
![]()
-
Побудуйте графік функції
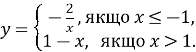
Користуючись графіком, укажіть проміжки зростання і проміжки спадання функції.
|
Контрольна робота 9 клас алгебра «Функція. Властивості функції» |
|||
|
Початковий рівень |
|||
|
Варіант 2
|
|||
|
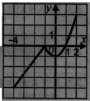
А) [-1; 3]; |
Б) (-3; 2); |
В) [-5; -4) |
Г) [-5;-4) |
проміжку [-4:2]. Користуючись графіком, знайдіть проміжки зростання функції.
|
|||
|
А) [-3; 3]; |
Б) [-2; 3]; |
В) [-3,5; 1]; |
Г)[-1;4]. |
рисунок.
|
|||
|
|||
|
Б) |
B) -8 |
Г) |
|
|
|||
|
А) [-1; 3]; |
Б) [-2; 2]; |
В) [1; 3]; |
Г) [-2; 1]. |
проміжок спадання функції.
|
|||
|
А) |
Б) |
В) |
Г) |
- Установіть відповідність між функцією (1-4) та її властивістю (А-Д).
|
1 |
|
А |
Нулі функції дорівнюють -5 і 5 |
|
2 |
|
Б |
Область визначення функції — (- |
|
3 |
|
В |
Графік функції проходить через точку (0;-5) |
|
4 |
|
Г |
Нулі функції дорівнюють 0 і 5 |
|
|
Д |
Область значень функції— [0;+ |
|
- Побудуйте на одній координатній площині графіки функцій
![]()
-
Побудуйте графік функції

Користуючись графіком, укажіть проміжки зростання і проміжки спадання функції.


про публікацію авторської розробки
Додати розробку

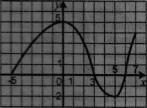
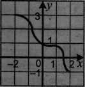 Укажіть область значень функції, визначеної на проміжку [-
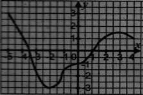
Укажіть область значень функції, визначеної на проміжку [-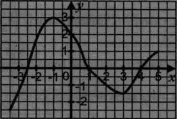 На рисунку зображено графік функції
На рисунку зображено графік функції