Конкурс "Найрозумніший математик"

Позакласний захід

Конкурс «Найрозумніший математик»

для учнів 7-х класів

Мета: розвивати пізнавальну активність, творчі здібності, винахідливість, 

     кмітливість учнів; виховувати цілеспрямованість, упевненість в собі,

     волю до перемоги, досягнення успіху у житті.

Обладнання: мультимедійна система, презентація, картки для   відповідей до І

               туру і дешифраторів

 

Передмова

           Гра – шлях дітей до пізнання світу, в якому

вони живуть і який вони покликані змінити.

О. М. Горький

     Всі зміни, що відбуваються в нашому суспільстві, перебудови, реформи, незмінним залишають одне: кожна дитина – особистість, і наше з Вами завдання допомогти розкрити всі грані цієї особистості. Кожен з нас шукає свої шляхи, підходи в реалізації даного завдання. Кожен з нас задає питання: «Як запалити іскру пізнавального інтересу в дітей? Як спонукати до творчого пошуку?»

   Одним з таких шляхів є організація і проведення інтелектуальних ігор для дітей. Саме через гру дитина може себе реалізувати, відкрити в собі нове. Під час гри виховується багато вольових якостей: самостійність, наполегливість, самовладання,  витримка, воля до перемоги ˗ усе те, без чого не може бути успіху. Адже наявність усіх цих умов становить основу всякої плідної праці. Гра ˗ це не лише розвага, що заповнює дозвілля школярів, але й один з найсерйозніших засобів педагогічного впливу на них. Участь у конкурсі «Найрозумніший» сприяє розвитку пізнавального інтересу учнів, спонукає їх до творчого пошуку, самовдосконалення.

   Конкурс «Найрозумніший» розроблений по принципу однойменної телепередачі. У  першому турі приймають участь 12 учнів, які дають відповідь на 18 обов’язкових питань. Кожне питання читається двічі, після цього учасники дають відповідь на заготовлених картках, які віддають журі (додаток 1). Ведучий після кожного питання відкриває правильну відповідь. Кожна правильна відповідь оцінюється в один бал. Визначаються шість учасників, які отримали найбільшу кількість балів і  вони переходять до другого туру. Результати І і ІІ турів чітко фіксуються (додаток 2). У другому турі шість учасників, яким пропонується шість категорій різної тематики. На початку другого туру проводимо дешифратор. Кожній цифрі у відповідність поставлений певний набір букв. Учасники розшифровують вказане слово. Хто перший розшифрує, той першим починає гру, і в нього можливість вибрати ту тему, яка йому найкраща. Завдання для кожного – за 1 хвилину дати якнайбільше правильних відповідей. По кількості балів троє учасників проходять до фіналу. На початку фіналу знову проводимо дешифратор, щоб визначитися з черговістю гравців. Якщо учасник відкриває питання і дає правильну відповідь, то отримує 2 бали, якщо відповідь неправильна – то 0 балів. По підсумках фіналу визначається переможець, який отримує титул «Найрозумніший математик».

   Презентацію до конкурсу Ви можете знайти за посиланням https://drive.google.com/file/d/0B3X4i5uY0ToURUJtLXlLWVJ0LXc/view?usp=sharing.

     Бажаю всім чудового інтелектуального дозвілля, а дітям отримати перемогу і здобути титул «Найрозумніший математик»!

 

Хід проведення

 

1. Вступне слово вчителя.

2. І тур.

3. ІІ тур.

4. Фінал.

5. Підведення підсумків конкурсу.

 

1. Доброго дня діти! Вітаю Вас на конкурсі найсміливіших, найкмітливіших юних математиків 7 класів! Попереду Вас чекають непрості випробування, тому будьте уважні, долайте труднощі і здобувайте перемогу у нашому конкурсі «Найрозумніший математик». З правилами гри Ви всі добре ознайомлені і можемо розпочинати наші змагання! Бажаю Вам успіхів і хай переможе найкращий!

2. І тур

1.               Скільки простих чисел більших за 8 і менших за 20? 

А  2;   Б  3;  В  4;  Г  5.

2.               Знайдіть серед виразів одночлен:

 

А  5 + х;  Б  3х² – у;  В    Г 

3.               Знайдіть 25% від 80.

 А  20;  Б  25;  В  30;  Г  35.

4.               Піднесіть до квадрату: (4х – 3)²

А  16х² – 9;  Б  16х² – 12х + 9;  В  16х² + 9;   Г  16х² – 24х + 9.

5.               Один із суміжних кутів 47⁰. Знайдіть другий.

А  43⁰;  Б  123⁰;   В  133⁰;  Г  143⁰.

6.               Обчисліть:

А   7;   Б  3;  В  -3;  Г  -7.

7.               Знайдіть степінь многочлена:

 А  4;  Б  3;  В  2;  Г  1.

8.               Знайдіть суму всіх цілих чисел від -9 до 10.

А  -9;  Б  1;  В  0;   Г  10.

9.               У якій країні виникли від’ємні числа?

А  Німеччині;  Б  Франції;  В  Італії;   Г  Китаї.

10.          Два числа називаються взаємно оберненими, якщо:

А  їхня сума дорівнює 1;  Б  їхня частка дорівнює 1;

В  їхній добуток дорівнює 0;   Г  їхній добуток дорівнює 1.

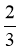11.          Іванко прочитав 120 сторінок, що становить       усієї книжки. Скільки сторінок у книзі?

А 80 сторінок;  Б  120 сторінок;   В  180 сторінок;  Г  210 сторінок.

12.          Модулем від’ємного числа називають:

А від’ємне число;   Б  протилежне йому число;

В  число 0;   Г  саме число.

13.          Обчисліть значення виразу: 2³ + 1³.

А  7;  Б  8;   В  9;  Г  11.

14.          Який кут утворює годинна і хвилинна стрілка о 16 годині?

 А  120⁰;  Б  100⁰;  В  90⁰;  Г  80⁰.

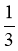
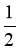15.          На яке число треба розділити 3, щоб отримати 6?

А       ;    Б      ;   В   2;   Г  3.

16.          На прямій розміщені точки. Відстань між першою і останньою 300 см, між кожними двома сусідніми точками 6 см. Скільки всього позначено точок?

А  48;  Б  50;   В  51;   Г  52.

17.          Який німецький математик ввів термін «функція»?

 А Лейбніц;   Б  Декарт;  В  Ейлер;  Г  Лагранж.

18.          Хто вперше запропонував знак ∆ для позначення трикутника?

А  Евклід;  Б  Кеплер;  В  Вейєрштрасс;   Г  Герон.

3. ІІ тур

 

 

 

 

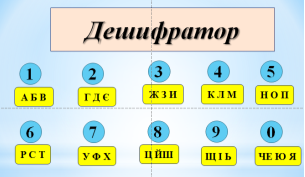
Завдання: так перекладається з латині слово «радіус»

5

6

5

4

9

5

9

п

р

о

м

і

н

ь

 

Розшифровка: 

Категорії

 

 

 

 

 

Подільність чисел

1.               Число, що є дільником всіх чисел.                                                     (1)
2.               Скільки дільників має число 8?                                                          (4)
3.               Найменше просте число.                                                                     (2)
4.               Якою цифрою закінчуються натуральні числа, які діляться на 5? (0; 5)
5.               Найбільший спільний дільник 12 і 16.                                              (4)
6.               Найменше спільне кратне 3 і 7.                                                          (21)
7.               На які числа ділиться число 2538?                                                     (2; 3; 9)
8.               Найбільший дільник числа 138.                                                          (138)
9.               Якщо число закінчується цифрою 0, то воно ділиться на …            (2; 5; 10)
10.          Найменший дільник числа 28.                                                               (1)
11.          Найменше кратне числа 28.                                                                   (28)
12.          Найменше двохцифрове число, яке ділиться на 2, 3 і 5.                      (30)
13.          Якою цифрою треба замінити а у виразі 7  а + 2,

           щоб отримане число ділилося на 3?                                                (1; 4; 7)

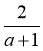14.          Якою цифрою треба замінити а у виразі            ,

           щоб отримати ціле число?                                                                   (0; 1)

15.          Найбільше двохцифрове число, що ділиться на 2 і 3.                           (96)

Цілі числа

1.               Найбільше ціле від’ємне число.                                                                (-1)
2.               Скільки цілих чисел розміщено між  -0,5 і 0,5?                                       (1)
3.               Обчисліть:  – 6 – 5.                                                                                    (-11)
4.               Обчисліть: – 2  (–2) – 4.                                                                            (0)
5.               Найменше трьохцифрове натуральне число, добуток цифр якого 3.   (113)
6.               Між якими цілими числами знаходиться число -1,8?                          (-2 і -1)
7.               Обчисліть: (-2)³.                                                                                         (-8)
8.               Обчисліть: (-1)²⁰¹⁶.                                                                                      (1)
9.               Найбільше ціле від’ємне двохцифрове число.                                          (10)
10.          Протилежне число до 12.                                                                          (-12)
11.          Знайдіть число, 25 % від якого дорівнює 8.                                             (32)
12.          Що більше  -10 чи -11?                                                                              (-10)
13.          Скільки натуральних чисел розміщено між -5 і 1?                          (Жодного)
14.          Обчисліть: 5²⁰¹⁶  0,2²⁰¹⁶.                                                                              (1)
15.          Знайдіть 50 % від 72.                                                                                  (36)

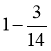
Дроби

1.               Який з дробів правильний:         чи        ?        
2.               Обчисліть:               .

 

3.               Обчисліть:             .                                                                                    (4)  

 

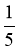4.               Обчисліть:            .                                                                                    (24)
5.               Перетворіть звичайний дріб       у десятковий.                                       (0,2)
6.               Скоротіть:          .  

 

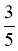
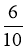7.               Який з дробів більший:           чи           ?                                        (Однакові)
8.               Обчисліть: 1 – 0, 36.                                                                                (0,64)
9.               Обчисліть: 3,5  100.                                                                              (350)
10.          Обчисліть:   3,5 : 10.                                                                               (0,35)
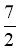
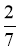11.          Округліть 2,37 до десятих.                                                                    (2,4)
12.          Як називаються дроби          і       ?                                       (Взаємно обернені)

 

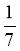
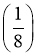
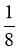
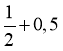13.          Знайдіть         від 9.                                                                                  (6)
14.          Який з дробів менший:       чи       ?   

 

15.          Обчисліть:                .                                                                                 (1)

 

Многочлени

1.               Розкладіть на множники: х² – 64.                                            (х – 8)(х – 8)
2.               Розкладіть на множники: 3х² + 3.                                            3(х² + 1)
3.               Назвіть степінь многочлена 3х – 5.                                           (1)
4.               Піднесіть до квадрату: (а – 6)².                                                 (а² – 12а + 36)
5.               Спростіть: 5х + 5х +5.                                                                (10х + 5)
6.               Зведіть до стандартного виду: 8х²  0,5х.                                 (4х³)
7.               Спростіть: (х⁴)³  х.                                                                      (х¹³)
8.               Розкладіть на множники: а² –20а + 100.                                  (а – 10)²
9.               Спростіть вираз: (9 + х)(9 – х).                                                  (81 – х²)
10.          Розкрийте дужки: 5х(х + 2).                                                      (5х² + 10х)
11.          Назвіть степінь многочлена: 8х³ – 4х⁴у.                                         (5)
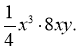12.          Розкладіть на множники: х² + 4.                                            (Не розкладається)
13.          Зведіть до стандартного виду:                                                      (2х⁴у)
14.          Розкладіть на множники: 4х – 4.                                                  (4(х – 1))
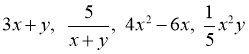
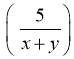15.          Який з цих виразів не є многочленом:

        ?

 

Трикутники

1.               Трикутник, у якого один кут прямий.                                    (Прямокутний)
2.               Відрізок, що з’єднує вершину трикутника із серединою

          протилежної сторони.                                                              (Медіана)

3.               Точка перетину бісектрис кутів трикутника.                           (Інцентр)
4.               Сума гострих кутів прямокутного трикутника.                        (90⁰)
5.               Трикутник, у якого дві сторони рівні.                                      (Рівнобедрений)
6.               Сума внутрішніх кутів трикутника.                                          (180⁰)
7.               Центр кола, описаного навколо прямокутного трикутника.

                                                                                                (Середина гіпотенузи)

8.               Сума зовнішніх кутів трикутника.                                             (360⁰)
9.               Точка перетину висот трикутника.                                          (Ортоцентр)
10.          Сума двох кутів трикутника 110⁰. Знайдіть третій кут.            (70⁰)
11.          Кут при вершині рівнобедреного трикутника 100⁰. Знайдіть кути при основі

         трикутника.                                                                                   (40⁰)

12.          Знайдіть сторону рівностороннього трикутника, периметр якого 36 см.

                                                                                                                (12 см)

13.          Зовнішній кут трикутника 130⁰. Чому дорівнює сума двох внутрішніх кутів,

         не суміжних з ним.                                                                         (130⁰)

14.          У прямокутному трикутнику катет, що лежить навпроти кута 30⁰ , дорівнює

          18 см. Знайдіть гіпотенузу.                                                           (36 см)

15.          Гіпотенуза прямокутного трикутника 24 см. Чому дорівнює медіана

          трикутника, проведена до гіпотенузи.                                          (12 см)

 

Геометричний аукціон

1.               Основні фігури планіметрії.                                         (Точка і пряма)
2.               Частина прямої, що лежить по один бік від даної точки.     (Промінь)
3.               У скількох точках перетинаються дві прямі?               (Одній)
4.               Два промені, що доповнюють один одного до прямої.  (Доповняльні)
5.               Частина площини, обмежена колом.                                (Круг)
6.               Фігура, що складається з точки і двох променів, що виходять з неї. (Кут)
7.               Пряма, що перетинає дві інші.                                         (Січна)
8.               Геометричне місце точок, рівновіддалених від сторін кута.  (Бісектриса)
9.               Відношення довжини кола до його діаметра.                  (Число π)
10.          Відрізок, що сполучає центр кола з будь-якою його точкою.  (Радіус)
11.          Пряма, що має з колом одну спільну точку.                             (Дотична)
12.          Кути, в яких одна сторона спільна, а дві інші – доповняльні промені.

                                                                                                        (Суміжні)

13.          Один з вертикальних кутів 56⁰. Чому дорівнює другий?        (56⁰)
14.          У скільки разів збільшиться кут 40⁰, якщо його сторони продовжити вдвічі?

                                                                                               (Не зміниться)

15.          Що більше: кут рівностороннього трикутника чи кут квадрата?

                                                                                                (Кут квадрата)

4. Фінал

Дешифратор

Завдання: термін «хорда» походить від грецького слова …

6

6

6

7

5

1

 

с

т

р

у

н

а

Розшифровка: 

 

   Перед дітьми ігрове поле із завданнями по темі «Математичні прислів’я»

 

 

 

 

 

 

 

Завдання

1.               Скільки разів не ввійдеш в одну річку?                                     (Двічі)
2.               Скільки разів потрібно відміряти, щоб один раз відрізати?    (Сім) 
3. Скільки чекають обіцяного?                                                   (3 роки) 
4.               За скількома зайцям ганяються у відомому  прислів’ї?    (За двома) 
5.               Скільки разів краще побачити, чим 100 разів почути?          (Один раз) 
6.               Яку кількість друзів краще мати, ніж 100 гривень?        (100 друзів) 
7.               Скільки разів платить скупий?                                         (Двічі) 
8.               Скільки людей одного не ждуть?                                        (7) 
9.               Скільки голів краще, ніж одна, згідно прислів’я?           (Дві) 
10.          Скільки гусей трави не витопче?                                 (Один)
11.          Скільки разів треба відміряти, щоб один раз відміряти?  (Десять)
12.          Якщо ідеш на день, то скільки треба брати харчів?    (На три дні)
13.          Одна голова добре, а скільки краще?                            (Дві)
14.          Жінка за три кути хату держить, а чоловік?                 (За один)
15.          Скільки ложок дьогтю  зіпсує бочку меду?                  (Одна)
16.          Одне літо ліпше, чим скільки зим?                               (Сто)

5. Підведення підсумків конкурсу.

Нагородження переможця титулом «Найрозумніший»

 

 

 

 

 

 

 

 

 

Додаток 1

 

1.	10.
А      Б      В        Г	А      Б      В        Г
2.	11.
А      Б      В        Г	А      Б      В        Г
3.	12.
А      Б      В        Г	А      Б      В        Г
4.	13.
А      Б      В        Г	А      Б      В        Г
5.	14.
А      Б      В        Г	А      Б      В        Г
6.	15.
А      Б      В        Г	А      Б      В        Г
7.	16.
А      Б      В        Г	А      Б      В        Г
8.	17.
А      Б      В        Г	А      Б      В        Г
9.	18.
А      Б      В        Г	А      Б      В        Г

 

 

 

 

 

 

 

Додаток 2

	І тур	ІІ тур	Фінал
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

 

 

 

 

 

 

 

 

 

 

 

 

Список використаних джерел

1.               Баран О. І. Математичні мініатюри / О. І. Баран. – Харків: Основа, 2003. – 96 с.
2.               Василенко О. О. Серенада математиці / О. О. Василенко. – Харків: Основа, 2003. – 123 с.
3.               Лисенко О. Є. Математичний бій. 7 клас [Електронний ресурс] / О. Є. Лисенко // 2015 – Режим доступу до ресурсу: https://drive.google.com/file/d/0B3X4i5uY0ToUVnFwMkQ4WWpxX2s/view?usp=sharing.
4.               Лисенко О. Є. Сильна ланка. 6 клас [Електронний ресурс] / О. Є. Лисенко. – 2014. – Режим доступу до ресурсу: https://drive.google.com/file/d/0B3X4i5uY0ToUbjA1YmpaX0htcE0/view?usp=sharingg.
5.               Панішева О. В. Математичні пасажі / О. В. Панішева. – Харків: Основа, 2010. – 191 с. – (Б-ка журналу \"Математика в школах України\"; 1(85)).