Конспект до уроку: "Графік лінійних рівнянь з двома змінними"

Урок 2. Конспект

 

Що є графіком лінійного рівняння ax+by=c?

Розглянемо лінійне рівняння  . Виразимо змінну у через змінну х.

by = – ax + c | ÷b y = −ax+c  y =− ^𝑎 𝑥 + ^𝑐 , b ≠ 0

                              𝑏            𝑏

Ми одержали лінійну функцію, графіком якої є пряма.

Тобто графіком рівняння ax+by=c, a≠0, b≠0 є пряма.

Оскільки пряма однозначно задається двома своїми точками, то для побудови прямої, яка є графіком лінійної функції, достатньо знайти координати двох точок графіка.

Отже, щоб побудувати графік лінійного рівняння ax + by = c з двома змінними треба:

1.     Взяти будь-які 2 значення х (х₁ та х₂) та знайти відповідні їм значення у (у₁ та у₂);

2.     Побудувати в координатній площині точку А (х₁у₁) та точну В (х₂у₂)

х	–2	4
у	10	–5

3. 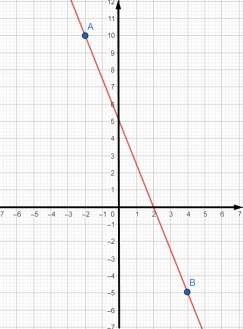    Через точки провести пряму.

Наприклад 1. Побудувати графік рівняння  

5х + 2у = 10                            

2у = 10 – 5х | ÷ 2 у = 5 – 2,5у

 

 

 

 

 

АБО!

 

 

 

х	0	2
у	5	0

Обрати точки перетину графіка з осями координат (0; у) – точка перетину з віссю х, (х; 0) – точка перетину з віссю у.

Тобто 5х + 2у = 10

Знайдемо точку перетину з осями:

з віссю О_х у = 0 х = 2 з віссю О_у х = 0 у = 5

 

 

 

 

 

Розглянемо окремі випадки лінійного рівняння.

Якщо лінійне рівняння ax + by = c, a = 0, b ≠ 0, то рівняння має вигляд by=c | ÷ b

c y =  b

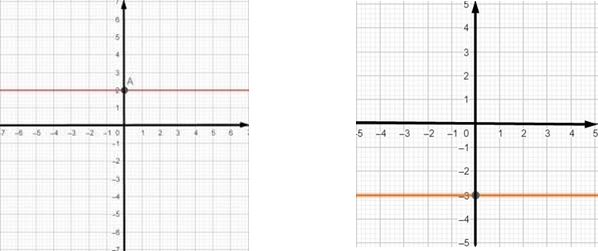
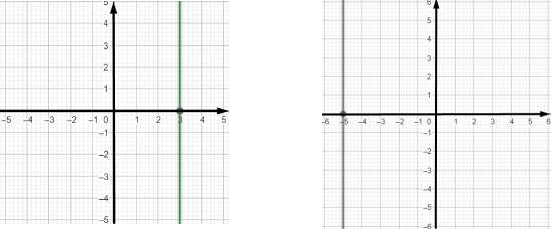
Графіком рівняння ax+by=c, a = 0, b ≠ 0 є пряма паралельна осі О_х, що

c проходить через точку ( 0;  ) b

 Наприклад 2, побудуйте графік рівняння 

а) 4у = 8                                                                     b) у = –3        у= 2

 

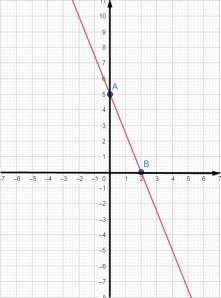
Якщо в лінійному рівняння  ax+by=c, a ≠0, b = 0, то рівняння має вигляд  ax = c| ÷ a

c

x =  , a ≠ 0. 

a Графіком рівняння ax+by=c, a ≠ 0, b = 0, є пряма паралельна осі О_у, що c проходить через точку ( ; 0). a

 Наприклад 3, побудуйте графік рівняння:

а) 3х = 9                                                  b) х = – 5        х = 3

 

 

 

Якщо в рівнянні ax + by=c, a = 0, b = 0, с = 0, то рівняння має вигляд 0х + 0у = 0, тобто будь-яка пара чисел є розв’язком цього рівняння, а його графіком є вся координатна площина.

Якщо в лінійному рівнянні   ax + by = c, a = 0, b = 0, с ≠ 0, тобто воно не має розв’язків отже його графік не містить жодної точки.

Давайте розв’яжемо разом:

1. Які з точок А (7; –4), В (5; – 2) належать графіку рівняння 7х + 5у = 25

Точка належить графіку рівняння якщо координати цієї точки є розв’язком даного рівняння.

А (7; –4)   Підставимо координати точки в рівняння 7х + 5у = 25

Маємо  7*7+5(–4) = 25

             49 – 20 = 25                      29 ≠ 25

Отже, точка А (7; –4) не належить графіку рівняння.

В (5; – 2)  Підставимл координати точки до рівняння

Маємо   7*5 + 5(–2) = 25

                     35 – 10 = 25

                             25 = 25

Отже, точка  В (5; – 2) належить графіку рівняння.

2. Побудуйте графік рівняння 

х	2	3
у	4	3

a)     х + у = 6

Нехай х = 2, тоді 2 + у = 6                                     у = 4

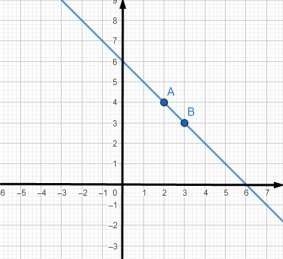Нехай х = 3, тоді  3 + у = 6                                      у = 3

 

 

 

 

 

 

 

 

 

 

 

 

х	–1	–2
у	6	4

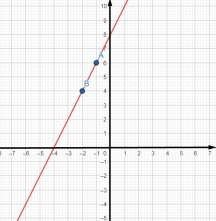
b)    x – 0.5y = 4                x + 4 = 0.5y | *2 y = 2x + 8 

 

c)     2x + 3y = 6

Знайдемо точку перетину графіка рівняння з осями координат.

з віссю О_х у = 0                         2х = 6           х = 3 з віссю О_у х = 0                          3у = 6           у = 2

х 0  3 у 2 0

 

Резюмування